浙江省龙游柯城江山2022年九年级学业水平适应性考试数学试卷

试卷更新日期：2022-06-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022的倒数是（）

A、 $\frac{1}{2022}$ B、 $- \frac{1}{2022}$ C、-2022 D、2202

查看试题解析
2. 2021年10月26日，我国神舟十三号载人航天飞船发射升空，2022年4月16日成功返回，3名航天员翟志刚、王亚平、叶光富在“天宫”空间站生活工作183天，已知“天宫”空间站每时绕地球大约飞行480000米，480000用科学记数法表示为（）

A、 $0.48 \times 1 0^{6}$ B、 $48 \times 1 0^{4}$ C、 $4.8 \times 1 0^{5}$ D、48

查看试题解析
3. 一个物体如图所示，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $3 a^{2} - a^{2} = 3$ B、 $a^{6} \div a^{2} = a^{4}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $(a + b)^{2} = a^{2} + b^{2}$

查看试题解析
5. 将分别标有数字2，3，x的三个球放入不透明的袋中，这些球除数字外都相同，搅匀后任意摸出一个球.若摸出球上的数字小于7是必然事件，则x的值可以是（）

A、11 B、9 C、7 D、5

查看试题解析
6. 不等式组 ${\begin{array}{l} 2 x + 2 \geq 4 \\ 9 - x > 2 x \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，BD是 $△ A B C$ 外接圆的直径， $B E ⊥ A C$ 于点E，连结 $C D$ ，若 $∠ A B E = 40 °$ ，则 $∠ C B D$ 的度数为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
8. 如图，在 $△ A B C$ 中，高 $A D$ 和 $B E$ 交于点F，添加下列哪个条件（），不能使得 $△ A D C ≌ △ B D F$ .

A、 $B F = A C$ B、 $C D = F D$ C、 $∠ B A D = 45 °$ D、 $∠ C B E = 60 °$

查看试题解析
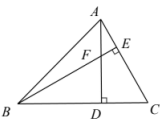9. 已知二次函数 $y = a x^{2} + b x + 3$ 经过点 $(2 ， 3)$ ，且函数最大值为4，则a的值为（）

A、 $- \frac{1}{2}$ B、-1 C、-2 D、 $- \frac{1}{3}$

查看试题解析
10. 如图，将矩形纸片 $A B C D$ 沿 $E F$ 、 $G N$ 折叠，使点A和点C重合于点M，点D与点H重合，点B落在边 $A D$ 上的点P处，且 $M N$ 经过点P.已知 $\frac{E P}{P G} = \frac{4}{3} ， F N = 10 c m$ ，则 $G D$ 的长为（）

A、 $\frac{42}{5} c m$ B、 $\frac{43}{5} c m$ C、 $\frac{44}{5} c m$ D、 $9 c m$

查看试题解析

二、填空题

11. 因式分解： $a^{2} - 9 =$ ．

查看试题解析
12. 冬奥会单板U型池比赛中，某单板滑雪运动员的成绩（单位：分）为81，89，83，88，84.则这组数据的中位数是.

查看试题解析
13. 已知正n边形的一个外角是45°，则n＝

查看试题解析
14. 如图是古希腊数学家埃拉托斯特尼在夏至日这天测量地球子午线周长的示意图，其中太阳光线 $A B ∥ C D ， C E$ 是竖直插在球面上的木杆， $A B ， C E$ 的延长线都经过圆心O.已知B，E间的劣弧长约为800千米，子午线周长约为40000千米，则 $∠ D C E$ 的度数约为 $°$ .

查看试题解析
15. 如图，在平面直角坐标系中， $△ A B C$ 各顶点均在反比例函数 $y = \frac{k}{x}$ 图象上， $A B$ 经过点O，延长 $A C$ 交x轴于点D， $A C = C D$ ，若 $△ A B C$ 的面积为12，则 $k =$ .

查看试题解析
16. 三折伞是我们生活中常用的一种伞，三折伞的骨架是一个“移动副”和多个“转动副”组成的连杆机构，如图1是三折伞一条骨架的结构图，当“移动副”（标号1）沿着伞柄移动时，折伞的每条骨架都可以绕“转动副”（标号2-9）转动：图2是三折伞一条骨架的示意图，其中四边形 $C D E F$ 和四边形 $D G M N$ 都是平行四边形， $A C = B C = 13 c m$ ， $D E = 2 c m$ ， $D N = 1 c m$ .

(1)、若关闭折伞后，点A、E、H三点重合，点B与点M重合，则 $B N =$ $c m$ .

(2)、在（1）的条件下，折伞完全撑开时， $∠ B A C = 75 °$ ，则点H到伞柄 $A B$ 距离是 $c m$ （结果精确到 $0.1 c m$ ）.（参考数据： $s i n 75 ° \approx 0.97 ， c o s 75 ° \approx 0.26 ， t a n 75 ° \approx 3.73$ ）

查看试题解析

三、解答题

17. 计算： $(2022)^{0} - 2 s i n 45 ° + | - 2 | - \sqrt{4}$

查看试题解析
18. 先化简，再求值： $\frac{x}{x - 1} - \frac{x^{2} + 1}{x^{2} - 1}$ ，其中 $x = 2$ .

查看试题解析
19. 如图，在 $▱ A B C D$ 中，过点A作 $A E ⊥ B C$ 于点E， $A F ⊥ D C$ 于点F，且 $A E = A F$ .

(1)、求证： $▱ A B C D$ 是菱形.

(2)、若 $∠ E A F = 60 ° ， D F = 2$ ，求平行四边形 $A B C D$ 的面积.

查看试题解析

20. 某校为了解学生对“有礼衢州”城市标签的了解程度，做了一次抽样调查，调查结果共分为四个等级：A.不了解：B.基本了解：C.比较了解；D.非常了解.根据调查统计结果，绘制了如下三种不完整的统计图表.请结合统计图表，回答下列问题：

	对“有礼衢州”的了解程度	百分比
$A$	不了解	5%
$B$	基本了解	$m %$
$C$	比较了解	45%
$D$	非常了解	35%

(1)、本次参与调查的学生共有人，

m =

(2)、求扇形统计图中扇形B的圆心角度数，并补全条形统计图（要求标注人数）.

(3)、该校为提高学生对“有礼衢州”城市标签的了解程度，准备开展关于“有礼衢州”城市标签的知识竞赛，九（4）班欲从3名男生和1名女生中任选2人参加比赛，请用列表或画树状图的方法，求出恰好选中“1男1女”的概率.

查看试题解析

21. 如图，以 $△ A B C$ 的边 $A B$ 为直径作 $⊙ O$ ，交边 $A C$ 于点D， $B C$ 为 $⊙ O$ 的切线，弦 $D E ⊥ A B$ 于点F，连结BE.

(1)、求证： $∠ A B E = ∠ C$ .

(2)、若点F为 $O B$ 中点，且 $O F = 1$ ，求线段 $B C$ 的长.

查看试题解析
22. 新冠疫情反弹以来，A市组织医疗队、B市组织物资队迅速支援C市，医疗队从A市出发匀速行驶，到B市装货，0.5小时后以相同的速度继续行驶，最终到达C市，物资队从B市出发匀速行驶到达C市.设医疗队行驶时间为 $x (h)$ ，医疗队与B市的距离为 $y_{1} (k m)$ ，物资队与B市的距离为 $y_{2} (k m)$ ， $y_{1}$ 、 $y_{2}$ 与x的函数关系如图所示.

(1)、求医疗队和物资队的行驶速度分别是多少？

(2)、物资队出发以后，当医疗队离B市距离为 $60 k m$ 时，求此时物资队离B市的距离.

(3)、当医疗队与物资队到B市的距离相等时，求医疗队行驶的时间.

查看试题解析
23. 如图1，在 $R t △ A C B$ 中， $∠ A C B = 90 ° ， C A = 6 ， C B = 8$ ，点E是中线 $C D$ 的中点.点P是边 $C B$ 上的动点（点P与点C不重合），点F，C关于直线 $A P$ 成轴对称，连结 $D F ， E F$ .小超为了研究点P运动过程中， $D F ， E F$ 之间的大小关系，借鉴了函数的学习经验，设 $P C = x$ ， $D F = y_{1} ， E F = y_{2}$ ，并利用几何画板画出如图2所示的 $y_{1} ， y_{2}$ 关于x的函数图象，且这两条函数图象的交点M的坐标约为 $(2.08 ， 1.73)$ .

(1)、求图1中DE的长.

(2)、写出图2中点M的实际意义及a的值.

(3)、结合图象，写出点P在运动过程中等腰 $△ D E F$ 的个数，并说明理由.

(4)、当 $y_{2} = E C$ 时，求x的值.

查看试题解析
24. 在正方形 $A B C D$ ， E，F分别是射线 $B C ， C D$ 上的点， $A E ⊥ B F$ 于点G.

(1)、如图1，若点E是 $B C$ 边上的点.求证： $C E = D F$ .

(2)、如图2，在（1）的条件下，延长 $B F$ 交 $A D$ 的延长线于点H，连结 $C H$ .若 $A B = 4 ， B E = 3$ ，求 $t a n ∠ B H C$ 的值.

(3)、延长BF交射线AD于点H，连结 $C G ， C H$ ，若 $\frac{C H}{C G} = k$ ，求 $\frac{C E}{B E}$ 的值（用含k的代数式表示）.

查看试题解析