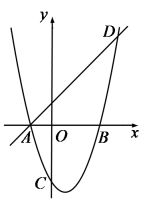广西梧州市藤县2022年九年级第一次模拟考试数学试卷
试卷更新日期:2022-06-07 类型:中考模拟
一、单选题
-
1. 在下列的数中,是负数的是( )A、1 B、3 C、-1 D、02. 将0.0069用科学记数法表示为( )A、 B、 C、 D、3. 不等式的解集是( )A、 B、 C、 D、4. 一个立体图形的三视图如图所示,则该立体图形是( )
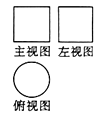 A、圆柱 B、圆锥 C、长方体 D、球5. 下列说法正确的是( )A、“三角形任意两边之和大于第三边”是不可能事件 B、了解一批灯泡的使用寿命,应采用全面调查 C、“明天的降水概率是80%”,是指明天有80%的时间在下雨 D、抛一枚质地均匀的硬币,正面朝上的概率为6. 某人沿坡度为的山路向上行走了30m,则该人升高了( )A、10m B、15m C、17m D、m7. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A、圆柱 B、圆锥 C、长方体 D、球5. 下列说法正确的是( )A、“三角形任意两边之和大于第三边”是不可能事件 B、了解一批灯泡的使用寿命,应采用全面调查 C、“明天的降水概率是80%”,是指明天有80%的时间在下雨 D、抛一枚质地均匀的硬币,正面朝上的概率为6. 某人沿坡度为的山路向上行走了30m,则该人升高了( )A、10m B、15m C、17m D、m7. 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )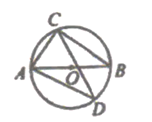 A、35° B、45° C、55° D、65°8. 已知一组从小到大排列的数据:的平均数与中位数都是6,则这组数据的众数是( )A、2 B、5 C、6 D、99. 近年来,快递业发展迅速,2018年我国快递业务量为507亿件,2020年预计快递量将达到700亿件,设快递量平均每年增长率为x.则下列方程中正确的是( )A、 B、 C、 D、10. 如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )
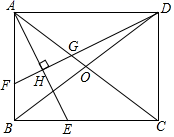
A、35° B、45° C、55° D、65°8. 已知一组从小到大排列的数据:的平均数与中位数都是6,则这组数据的众数是( )A、2 B、5 C、6 D、99. 近年来,快递业发展迅速,2018年我国快递业务量为507亿件,2020年预计快递量将达到700亿件,设快递量平均每年增长率为x.则下列方程中正确的是( )A、 B、 C、 D、10. 如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( ) A、 B、 C、 D、11. 如图,在▱ABCD中,将△ABD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为( )
A、 B、 C、 D、11. 如图,在▱ABCD中,将△ABD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为( )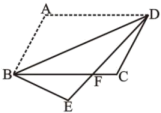 A、112° B、118° C、120° D、122°12. 如图,抛物线 与 轴交于 、 两点, 是以点 (0,3)为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是( )
A、112° B、118° C、120° D、122°12. 如图,抛物线 与 轴交于 、 两点, 是以点 (0,3)为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 的倒数是 .
14. 分解因式:15. 如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为 .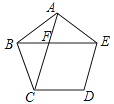 16. 如图,在Rt△ABC中,AC的垂直平分线DE交AC于点D, 交BC于点E,∠BAE=20°,则∠DCE的度数是为.
16. 如图,在Rt△ABC中,AC的垂直平分线DE交AC于点D, 交BC于点E,∠BAE=20°,则∠DCE的度数是为.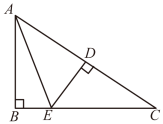 17. 在△ABC中,已知AB=6,BC=7,∠ABC=22°,则△ABC的面积等于.(参考数据:sin22°≈0.37, cos22°≈0.93, tan22°≈0.40,结果保留整数)18. 找规律数:0,6,16,30,48,…,则第个为(用含n的代数式表示).19. +sin30°﹣
17. 在△ABC中,已知AB=6,BC=7,∠ABC=22°,则△ABC的面积等于.(参考数据:sin22°≈0.37, cos22°≈0.93, tan22°≈0.40,结果保留整数)18. 找规律数:0,6,16,30,48,…,则第个为(用含n的代数式表示).19. +sin30°﹣三、解答题
-
20. 解一元一次方程:21. 已知双曲线与直线相交于A(-3,m)、B两点.(1)、直接写出此双曲线的解析式;(2)、若点M(a,b),且a,b都是不大于3的正整数,用画树状图法或列表法求点M在双曲线上的概率.22. 已知关于x的分式方程无解.(1)、求a的值;(2)、先化简,后求值:.23. 如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于点O,D为AB上的一点,OD=OC,以O为圆心,OB的长为半径作⊙O.
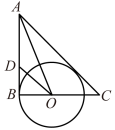 (1)、求证:AC是⊙O的切线;(2)、若AB=6,BD=2,求线段AC的长.24. 由甲、乙两人共同完成某公园1000m2的花圃的修剪工作,甲每天能完成100m2 , 乙每天能完成50m2.已知甲工作天,乙工作天,恰好完成此次修剪任务.(1)、求与的函数表达式;(2)、如果甲、乙两人工作天数总和不超过15天,求的取值范围;(3)、设此项修剪工作花费的人工费为w元,甲人工费需260元/天,乙人工费需120元/天,在(2)的条件下,求完成此项修剪工作所需的最低人工费.
(1)、求证:AC是⊙O的切线;(2)、若AB=6,BD=2,求线段AC的长.24. 由甲、乙两人共同完成某公园1000m2的花圃的修剪工作,甲每天能完成100m2 , 乙每天能完成50m2.已知甲工作天,乙工作天,恰好完成此次修剪任务.(1)、求与的函数表达式;(2)、如果甲、乙两人工作天数总和不超过15天,求的取值范围;(3)、设此项修剪工作花费的人工费为w元,甲人工费需260元/天,乙人工费需120元/天,在(2)的条件下,求完成此项修剪工作所需的最低人工费.