广西钦州市2022年中考一模数学试卷
试卷更新日期:2022-06-07 类型:中考模拟
一、单选题
-
1. 下列各数是无理数的是( )A、- B、0 C、2 D、π2. 下列立体图形中,俯视图与主视图完全相同的是( )A、
 B、
B、 C、
C、 D、
D、 3. “人教版数学九年级上册课本共154页,翻开该课本,恰好翻到第30页”,这个事件是( )A、必然事件 B、确定事件 C、不可能事件 D、随机事件4. 某冠状病毒的直径约为0.000000125米,其中数据0.000000125用科学记数法表示为( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. ,甲,乙两辆汽车即将经过该丁字路口,它们各自可能向左转或向右转,且两种情况的可能性相等,则它们经过丁字路口时,都向右转的概率为( )
3. “人教版数学九年级上册课本共154页,翻开该课本,恰好翻到第30页”,这个事件是( )A、必然事件 B、确定事件 C、不可能事件 D、随机事件4. 某冠状病毒的直径约为0.000000125米,其中数据0.000000125用科学记数法表示为( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. ,甲,乙两辆汽车即将经过该丁字路口,它们各自可能向左转或向右转,且两种情况的可能性相等,则它们经过丁字路口时,都向右转的概率为( ) A、 B、 C、 D、7. 在平面直角坐标系中,若点(3,2)与点(m,-2)关于原点对称,则m的值是( )A、2 B、-2 C、3 D、-38. 如图,AB是半圆O的直径,CD为半圆O的弦,且 , , 则∠ACD的大小为( )
A、 B、 C、 D、7. 在平面直角坐标系中,若点(3,2)与点(m,-2)关于原点对称,则m的值是( )A、2 B、-2 C、3 D、-38. 如图,AB是半圆O的直径,CD为半圆O的弦,且 , , 则∠ACD的大小为( )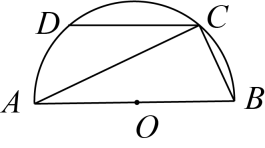 A、 B、 C、 D、9. 如图,是反比例函数在第一象限内的图象,且经过点A(1,2). 关于x轴对称的图象为 , 那么的函数解析式为( )
A、 B、 C、 D、9. 如图,是反比例函数在第一象限内的图象,且经过点A(1,2). 关于x轴对称的图象为 , 那么的函数解析式为( ) A、 B、 C、 D、10. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发x日,甲乙相逢,可列方程( )A、 B、 C、 D、11. 如图,小刚要测量斜坡CD旁一颗树AB的高度,已知在坡脚C处测得树顶B的仰角为 , 在坡顶D测得树顶B的仰角为 , 若 , , 则树AB的高是( )
A、 B、 C、 D、10. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲出发几日,甲乙相逢?设甲出发x日,甲乙相逢,可列方程( )A、 B、 C、 D、11. 如图,小刚要测量斜坡CD旁一颗树AB的高度,已知在坡脚C处测得树顶B的仰角为 , 在坡顶D测得树顶B的仰角为 , 若 , , 则树AB的高是( ) A、5m B、 C、15m D、10m12. 定义一种运算:则函数的图象大致是( )A、
A、5m B、 C、15m D、10m12. 定义一种运算:则函数的图象大致是( )A、 B、
B、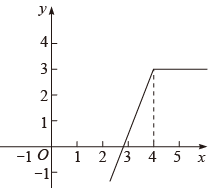 C、
C、 D、
D、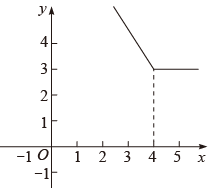
二、填空题
-
13. -2的绝对值是14. 因式分解: =.15. 某校4个绿化小组一天植树的棵数如下:8,9,11,12,那么这组数据的方差是.16. 如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面周长为8cm,侧面积为48cm2 , 则这个扇形的圆心角的度数是.
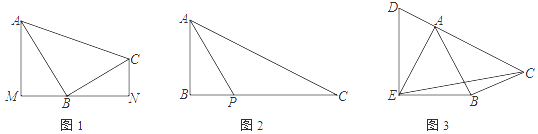
 17. 关于抛物线(k为常数),下列结论:①开口向上;②顶点不可能在第三,四象限;③若点是抛物线上的两点,则;④当k取任意实数时,顶点所在的曲线为.其中一定正确的是(填序号即可).18. 如图,在△ABC中, , BC=3,AC=4,点D是AC边上一动点,过点A作交BD的延长线于点E,则的最小值为.
17. 关于抛物线(k为常数),下列结论:①开口向上;②顶点不可能在第三,四象限;③若点是抛物线上的两点,则;④当k取任意实数时,顶点所在的曲线为.其中一定正确的是(填序号即可).18. 如图,在△ABC中, , BC=3,AC=4,点D是AC边上一动点,过点A作交BD的延长线于点E,则的最小值为.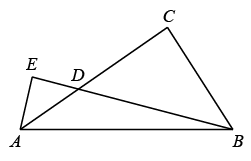
三、解答题
-
19. 计算:.20. 不等式组:并用数轴表示不等式组的解集.
 21. 如图,在四边形ABCD中,已知 , AE平分∠BAC,且 , .
21. 如图,在四边形ABCD中,已知 , AE平分∠BAC,且 , .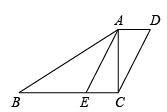 (1)、求证:;(2)、尺规作图:过点E作垂线 , 垂足为F(不要求写作法,保留作图痕迹);(3)、在(2)的条件下,已知四边形AECD面积为12, , 直接写出线段EF的长.22. 某校开展了“学党史,知党恩,跟党走”的知识竞赛.现从该校七、八年级中各随机抽取20名学生的竞赛成绩进行调查:
(1)、求证:;(2)、尺规作图:过点E作垂线 , 垂足为F(不要求写作法,保留作图痕迹);(3)、在(2)的条件下,已知四边形AECD面积为12, , 直接写出线段EF的长.22. 某校开展了“学党史,知党恩,跟党走”的知识竞赛.现从该校七、八年级中各随机抽取20名学生的竞赛成绩进行调查:【收集数据】
七年级:70,74,74,76,78,78,80,80,82,85,88,88,94,95,98,100,100,100,100,100;
八年级:64,68,70,72,74,80,82,82,84,86,90,92,98,98,100,100,100,100,100,100
【分析数据】两组数据的平均数、众数、中位数如表:
年级
平均数
众数
中位数
七年级
87
100
a
八年级
87
b
88
根据以上信息,解答下列问题:
(1)、直接写出上述表格中a,b的值;(2)、根据以上样本数据,你认为该校七、八年级中哪个年级学生对“党史”掌握较好?请说明理由;(3)、若成绩在80分以上(含80分)为优秀,该校七、八年级共有800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?23. 如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H. (1)、若连接AO,试判断四边形AECO的形状,并说明理由;(2)、求证:AH是⊙O的切线;(3)、若AB=6,CH=2,则AH的长为.24. 跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为抛物线.如图是甲,乙两人将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为1m,并且相距4m,现以两人的站立点所在的直线为x轴,过甲拿绳子的手作x轴的垂线为y轴,建立如图所示的平面直角坐标系,且绳子所对应的抛物线解析式为.
(1)、若连接AO,试判断四边形AECO的形状,并说明理由;(2)、求证:AH是⊙O的切线;(3)、若AB=6,CH=2,则AH的长为.24. 跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为抛物线.如图是甲,乙两人将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为1m,并且相距4m,现以两人的站立点所在的直线为x轴,过甲拿绳子的手作x轴的垂线为y轴,建立如图所示的平面直角坐标系,且绳子所对应的抛物线解析式为. (1)、求绳子所对应的抛物线解析式(不要求写自变量的取值范围);(2)、身高1.70m的小明,能否站在绳子的正下方,让绳子通过他的头顶?(3)、身高1.64m的小军,站在绳子的下方,设他距离甲拿绳子的手sm,为确保绳子能通过他的头顶,请求出s的取值范围.
(1)、求绳子所对应的抛物线解析式(不要求写自变量的取值范围);(2)、身高1.70m的小明,能否站在绳子的正下方,让绳子通过他的头顶?(3)、身高1.64m的小军,站在绳子的下方,设他距离甲拿绳子的手sm,为确保绳子能通过他的头顶,请求出s的取值范围.