广西贺州市平桂区2022年中考一模数学试卷
试卷更新日期:2022-06-07 类型:中考模拟
一、单选题
-
1. 下列实数是负数的是( ).A、 B、0 C、 D、12. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图形是轴对称图形而不是中心对称图形的是( ).A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图形是轴对称图形而不是中心对称图形的是( ).A、 B、
B、 C、
C、 D、
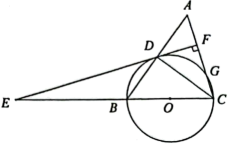
D、 5. 一组数据:3,4,5,4,6,这组数据的众数是( )A、3 B、4 C、5 D、66. 点关于y轴对称点的坐标为( ).A、 B、 C、 D、7. 原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了170万年误差不超过1秒.数据170万用科学记数法表示( )A、 B、 C、 D、8. 已知 , , 则∠BOC的度数为( )A、78° B、42° C、78°或42° D、102°或48°9. 若代数式在实数范围内有意义,则x的取值范围是( ).A、 B、 C、且 D、且10. 如图,在⊙O中,直径 , 弦于点C,若 , 则BC的长为( )
5. 一组数据:3,4,5,4,6,这组数据的众数是( )A、3 B、4 C、5 D、66. 点关于y轴对称点的坐标为( ).A、 B、 C、 D、7. 原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了170万年误差不超过1秒.数据170万用科学记数法表示( )A、 B、 C、 D、8. 已知 , , 则∠BOC的度数为( )A、78° B、42° C、78°或42° D、102°或48°9. 若代数式在实数范围内有意义,则x的取值范围是( ).A、 B、 C、且 D、且10. 如图,在⊙O中,直径 , 弦于点C,若 , 则BC的长为( ) A、 B、 C、1 D、211. 如图,在中, , , 将绕点A逆时针转60°得到 , 则的长是( )
A、 B、 C、1 D、211. 如图,在中, , , 将绕点A逆时针转60°得到 , 则的长是( ) A、 B、 C、 D、12. 在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数——“好数”.定义:对于三位自然数n,各位数字都不为0,且百位数字与十位数字之和恰好能被个位数字整除,则称这个自然数n为“好数”.例如:426是“好数”,因为4,2,6都不为0,且 , 6能被6整除;643不是“好数”,因为 , 10不能被3整除.则百位数字比十位数字大5的所有“好数”的个数是( )A、8 B、7 C、6 D、5
A、 B、 C、 D、12. 在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数——“好数”.定义:对于三位自然数n,各位数字都不为0,且百位数字与十位数字之和恰好能被个位数字整除,则称这个自然数n为“好数”.例如:426是“好数”,因为4,2,6都不为0,且 , 6能被6整除;643不是“好数”,因为 , 10不能被3整除.则百位数字比十位数字大5的所有“好数”的个数是( )A、8 B、7 C、6 D、5二、填空题
-
13. 因式分解:x2+2x=14. 某老师对九年级1班55名学生的数学成绩进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在80分及以上的学生有名.
 15. 不等式的正整数解是.16. 如图,点C、D分别是半圆AOB上的三等分点.若阴影部分的面积是 , 则半圆的半径OA的长为.
15. 不等式的正整数解是.16. 如图,点C、D分别是半圆AOB上的三等分点.若阴影部分的面积是 , 则半圆的半径OA的长为.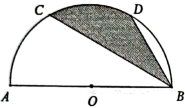 17. 如图,直线与抛物线交于点和点 , 若 , 则x的取值范围是.
17. 如图,直线与抛物线交于点和点 , 若 , 则x的取值范围是. 18. 如图,边长为2的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿DF直线折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM的长为.
18. 如图,边长为2的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿DF直线折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM的长为.
三、解答题
-
19. 计算:.20. 解方程:.21. 动画片(小猪佩奇)风靡全球,深受孩子们喜爱,现有4张(小猪佩奇)角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同),姐弟两人抽卡片,他们将这四张卡片混在一起,背面朝上放好.(1)、弟弟从中随机抽取一张卡片,恰好抽到B乔治的概率为;(2)、若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的方法求出他俩抽出的卡片是A佩奇,B乔治的概率.22. 已知甲楼AB高12米,自甲楼楼顶B处看乙楼楼顶D的仰角为25°,看乙楼楼底C的俯角为40°,现要在两楼楼顶B、D之间拉一条绳子挂小彩旗.(参考数据: , , , )
 (1)、求乙楼CD的高度;(结果精确到1米)(2)、现有一条20米的绳子,请问是否够长?23. 如图,在中,AD是BC边上的中线,E是AD的中点,过点A作交BE的延长线于点F,连接CF.
(1)、求乙楼CD的高度;(结果精确到1米)(2)、现有一条20米的绳子,请问是否够长?23. 如图,在中,AD是BC边上的中线,E是AD的中点,过点A作交BE的延长线于点F,连接CF. (1)、求证:;(2)、若 , , 求四边形ADCF的周长.24. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、当每件商品降价多少元时,该商店每天销售利润为1200元?(2)、该商店每天的利润能否达到1300元?
(1)、求证:;(2)、若 , , 求四边形ADCF的周长.24. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、当每件商品降价多少元时,该商店每天销售利润为1200元?(2)、该商店每天的利润能否达到1300元?