浙江省2022年普通高中数学1月学业水平考试试卷
试卷更新日期:2022-06-07 类型:高考真卷
一、选择题(本大题共18小题,每小题3分,共54分,每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
-
1. 已知集合P={0,1,2},Q={1,2,3},则P∩Q=( )A、{0} B、{0,3} C、{1,2} D、{0,1,2,3}2. 函数 的定义域是( )A、 B、 C、R D、3. 函数 的图象大致是()A、
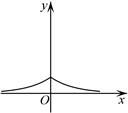 B、
B、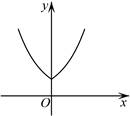 C、
C、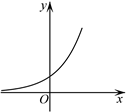 D、
D、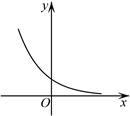 4. 已知α∈R,则cos(π-α)=()A、sinα B、-sinα C、cosα D、-cosα5. 已知圆M的方程为 ,则圆心M的坐标是( )A、( ,2) B、(1,2) C、(1, ) D、( , )6. 某几何体的三视图如图所示,则这个几何体可能是()
4. 已知α∈R,则cos(π-α)=()A、sinα B、-sinα C、cosα D、-cosα5. 已知圆M的方程为 ,则圆心M的坐标是( )A、( ,2) B、(1,2) C、(1, ) D、( , )6. 某几何体的三视图如图所示,则这个几何体可能是() A、棱柱 B、圆柱 C、圆台 D、球7. 已知函数 ( ),则此函数是()A、偶函数且在(-∞,+∞)上单调递减 B、偶函数且在(-∞,+∞)上单调递增 C、奇函数且在(-∞,+∞)上单调递减 D、奇函数且在(-∞,+∞)上单调递增8. 不等式 的解集是()A、 B、 C、 D、9. 设A,B是平面上距离为4的两个定点,若该平面上的动点P满足||PA|-|PB||=3,则P点的轨迹是()A、圆 B、椭圆 C、双曲线 D、抛物线10. 不等式组 表示的平面区域是()A、
A、棱柱 B、圆柱 C、圆台 D、球7. 已知函数 ( ),则此函数是()A、偶函数且在(-∞,+∞)上单调递减 B、偶函数且在(-∞,+∞)上单调递增 C、奇函数且在(-∞,+∞)上单调递减 D、奇函数且在(-∞,+∞)上单调递增8. 不等式 的解集是()A、 B、 C、 D、9. 设A,B是平面上距离为4的两个定点,若该平面上的动点P满足||PA|-|PB||=3,则P点的轨迹是()A、圆 B、椭圆 C、双曲线 D、抛物线10. 不等式组 表示的平面区域是()A、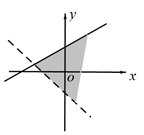 B、
B、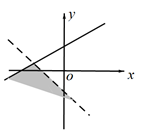 C、
C、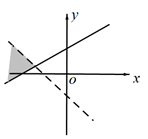 D、
D、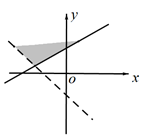 11. 已知空间中两条不重合的直线 ,则“ 与 没有公共点”是“ ”的()A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件12. 为了得到函数 的图象,可以将函数 的图象()A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度13. 已知函数 在区间(-∞,1]是减函数,则实数a的取值范围是()A、[1,+∞) B、(-∞,1] C、[-1,+∞) D、(-∞,-1]14. 已知向量 满足 ,则 ( )A、2 B、 C、8 D、15. 如图,正方体 中,N是棱 的中点,则直线CN与平面 所成角的正弦值等于( )
11. 已知空间中两条不重合的直线 ,则“ 与 没有公共点”是“ ”的()A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件12. 为了得到函数 的图象,可以将函数 的图象()A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度13. 已知函数 在区间(-∞,1]是减函数,则实数a的取值范围是()A、[1,+∞) B、(-∞,1] C、[-1,+∞) D、(-∞,-1]14. 已知向量 满足 ,则 ( )A、2 B、 C、8 D、15. 如图,正方体 中,N是棱 的中点,则直线CN与平面 所成角的正弦值等于( )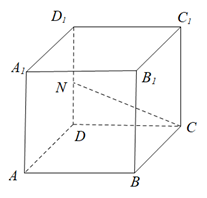 A、 B、 C、 D、16. 若 对任意 恒成立,则 的取值范围是()A、 B、 C、 D、17. 已知单位向量 不共线,且向量 满足 若 对任意实数λ都成立,则向量 夹角的最大值是()A、 B、 C、 D、18. 通过以下操作得到一系列数列:第1次,在2,3之间插入2与3的积6,得到数列2,6,3;第2次,在2,6,3每两个相邻数之间插入它们的积,得到数列2,12,6,18,3;类似地,第3次操作后,得到数列:2,24,12,72,6,108,18,54,3.按上述这样操作11次后,得到的数列记为 ,则 的值是()A、6 B、12 C、18 D、108
A、 B、 C、 D、16. 若 对任意 恒成立,则 的取值范围是()A、 B、 C、 D、17. 已知单位向量 不共线,且向量 满足 若 对任意实数λ都成立,则向量 夹角的最大值是()A、 B、 C、 D、18. 通过以下操作得到一系列数列:第1次,在2,3之间插入2与3的积6,得到数列2,6,3;第2次,在2,6,3每两个相邻数之间插入它们的积,得到数列2,12,6,18,3;类似地,第3次操作后,得到数列:2,24,12,72,6,108,18,54,3.按上述这样操作11次后,得到的数列记为 ,则 的值是()A、6 B、12 C、18 D、108二、填空题(本大题共4小题,每空3分,共15分)
-
19. 若数列 通项公式为 ,记前n项和为 ,则 ; .20. 在△ABC中,角A,B,C所对的边分别为a,b,c.若a=2,A=45°,B=60°,则b=.21. 设椭圆 的左、右焦点分别为 .已知点 ,线段 交椭圆于点P,O为坐标原点.若 ,则该椭圆的离心率为.22. 如图,E,F分别是三棱锥V-ABC两条棱AB,VC上的动点,且满足 则 的最小值为.

三、解答题(本大题共3小题,共31分)
