重庆市南渝2022年小升初数学试卷

试卷更新日期：2022-06-06 类型：小升初真题

进入出卷网下载

一、填空题（共42分）

1. 观察规律： $\frac{1}{2}$ ， $\frac{3}{5}$ ， $\frac{5}{8}$ ， $\frac{7}{11}$ ， $\frac{9}{14}$ ……这列数从左到右第100个数是。

查看试题解析
2. 若四位数2ABC能被13整除，则A+B+C的最大值是。

查看试题解析
3. 车前轮的周长是 $1 \frac{1}{3}$ 米，后轮的周长是 $1 \frac{1}{2}$ 米，则当前轮比后轮多转25圈时，自行车行走了米。

查看试题解析
4. 定义a*b=2× { $\frac{a}{2}$ }+3×{ $\frac{a + b}{6}$ }，其中符号{x}表示x的小数部分，如{2.016}=0.016．那么，1.4*3.2=。[结果用小数表示]

查看试题解析
5. 时钟显示9：15，此时分针与时针的夹角是度。

查看试题解析
6. 如图，在正方形ABCD中，点E在边AD上，AE=3ED，点F在边DC上，当S_△BEF最小时，S_△BEF：S_{正方形ABCD}的值是。

查看试题解析
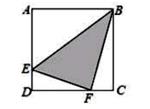7. 如图，三张卡片的正面各有一个数，它们的反面分别写有质数m，n，p，若三张卡片正反两面的两个数的和都相等，则m+n+p的最小值是。

查看试题解析
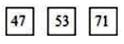8. 3²⁰¹⁴+4²⁰¹⁵+5²⁰¹⁶的个位数字是（注：a^m表示m个a相乘）

查看试题解析
9. 如图是由5个相同的正方形拼接而成，其中点B、P、C在同一直线上，点B、N、F在同一条直线上，若直线BF左侧阴影部分的面积是直线BF右侧阴影部分的面积的2倍，则MN：NP=。

查看试题解析
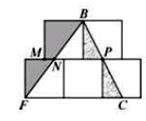10. 在如图所示的10×12的网格图中，猴子KING的图片是由若干圆弧和线段组成，其中最大的圆的半径是4，图中阴影部分的面积是。（圆周率π取3）

查看试题解析
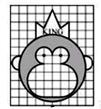11. 若2^a×3^b×5^c×7^d=252000，则从自然数a、b、c、d中任取3个组成三位数，这个三位数可被3整除并且小于250的概率是。

查看试题解析
12. 有一项工程，甲单独做需要6小时，乙单独做需8小时，丙单独做需10小时，上午8时三人同时开始，中间甲有事离开，如果到中午12 点工程才完成，则甲离开的时间是上午时分。

查看试题解析
13. 已知四位数ABCD，甲、乙、丙三人的结论如下：
甲：“个位数字是百位数字的一半”：

乙：“十位数字是百位数字的1.5倍”；

丙：“四个数字的平均数是4”。

根据上面的信息可得：ABCD=。

查看试题解析
14. 用棱长为m的小正方体拼成一个棱长为12的大正方体，现将大正方体的表面（6个面）涂成红色，其中只有一个面是红色的小正方体与只有两个面是红色的小正方体的个数相等，则m=。

查看试题解析

二、计算题（共24分）

15. 计算题
① $26 + 10.5 \times \frac{4}{5} \div 8 \frac{2}{5} - (26 - 1.6 \div \frac{4}{25} \times 2 \frac{1}{2})$

② $\frac{9}{13} \times \frac{47}{49} + 2 \div \frac{49}{47} \times \frac{1}{3} + (\frac{1}{3} + \frac{7}{13}) \times \frac{25}{49}$

③ $38 - [23.5 \div 2 \frac{2}{3} - (6.3 - 5 \frac{37}{40}) + 7.5 \times 0.375] \times \frac{8}{45}$

④ $(\frac{6}{11} + 1 \frac{3}{7} + \frac{8}{9}) \div (\frac{5}{7} + \frac{3}{11} + \frac{4}{9} ）$

⑤ $（ 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{2015} - \frac{1}{2016}) \div (\frac{1}{1009} + \frac{1}{1010} + ... + \frac{1}{2016})$

⑥ $\frac{2 x}{0.03} + \frac{65}{0.3} - \frac{14 - 3 x}{0.02} = 0$

查看试题解析

三、几何题（共4分）

16. 如图，两个半径相等的圆A和圆B相交，三角形DBC是等腰直角三角形，面积是24平方厘米，ABDC是平行四边形。图中阴影部分的面积是多少平方厘米？

查看试题解析

四、解决问题（共30分）

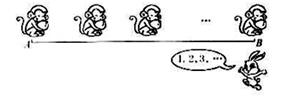
17. 用甲、乙、丙三个排水管排水，甲管排出1立方米水的时间，乙管能排出1.25立方米的水，丙管能排出1.5立方米的水现在要排完某个水池的水，先开甲管，2小时后开乙管，几小时后再开丙管，到下午4时正好把水排完，且各个排水管排出的水量正好相等。问什么时候打开的丙管？

查看试题解析
18. 有一台机器，使用了一种类型的零件1000个，一周内报废的零件在本周末换新零件在新零件中有10%在第一周末报废，有30%在第二周报废，有60%在第三周末报废，没有能使用四周以上的零件。

(1)、新机器中必须在第二周末换新的零件的个数是多少？

(2)、新机器中必须在第三周末换新零件的个数是多少？

查看试题解析
19. 张先生向商店订购某种商品80件，每件定价100元。张先生向商店经理说：“如果你肯减价，每减价1元，我就多订购4件。商品店经理算了一下，如果减价5%，由于张先生多订购，仍可获得与原来一样多的利润。问这种商品的成本是多少元？

查看试题解析
20. 汽车拉力赛有两个距离相等的赛程第一赛程由平路出发，离中点26千米的地方开始上坡：通过中点行驶4千米后，全是下坡路：第二个赛程也是由平路出发，离中点4千米处开始下坡：通过中点继续前进行驶26千米后，全是上坡路。已知某赛车在这两个赛程中所用的时间相同，第二个赛程出发时的速度是第一赛程出发是速度的 $\frac{5}{6}$ ，而遇到上坡时速度就要减慢25%，遇到下坡时速度就要增加25%。那么，每个赛程的距离各是多少千米？

查看试题解析
21. 有一群猴子要将A地的桃子搬运到B地，每隔3分钟有一只猴子从A地出发走向B地，全程需要12分钟，有一只兔子从B地跑步到A地，它出发的时候，恰有一只猴子到达B地，在路上它又遇到了5只迎面走来的猴子，继续向前到达A地，这时候，恰好又有一只猴子从A地出发，若兔子跑步的速度是3千米/小时，则A、B两地相距多少千米？

查看试题解析