（北师大版）2021-2022学年度第二学期七年级数学第六章概率初步 期末复习测试卷
试卷更新日期：2022-06-06 类型：复习试卷
一、单选题
-
1. 下列事件中，是必然事件的是（ ）A、掷一次骰子，向上一面的点数是2 B、买一张电影票座位号是奇数 C、菱形的对角线互相垂直 D、射击运动员射击一次，命中靶心2. 下列事件中，是必然事件的是（ ）A、掷一枚质地均匀的骰子，掷出的点数不超过6； B、一个射击运动员每次射击的命中环数； C、任意买一张电影票，座位号是2的倍数； D、早上的太阳从西方升起3. “抚顺市明天降雪的概率是70%”，对此消息，下列说法中正确的是（ ）A、抚顺市明天将有70%的地区降雪 B、抚顺市明天将有70%的时间降雪 C、抚顺市明天降雪的可能性较大 D、抚顺市明天肯定不降雪4. 做随机抛掷一枚纪念币的试验，得到的结果如下表所示：
抛掷次数m
500
1000
1500
2000
2500
3000
4000
5000
“正面向上”的次数n
265
512
793
1034
1306
1558
2083
2598
“正面向上”的频率
0.530
0.512
0.529
0.517
0.522
0.519
0.521
0.520
下面有3个推断：
①当抛掷次数是1000时，“正面向上”的频率是0.512，所以“正面向上”的概率是0.512；
②随着试验次数的增加，“正面向上”的频率总在0.520附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.520；
③若再次做随机抛掷该纪念币的实验，则当抛掷次数为3000时，出现“正面向上”的次数不一定是1558次．其中所有合理推断的序号是（ ）
A、② B、①③ C、②③ D、①②③5. 一个不透明的盒子里装有120个红、黄两种颜色的小球，这些球除颜色外其他完全相同，每次摸球前先将盒子里的球摇匀任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球试验后发现，摸到黄球的频率稳定在0.3，那么估计盒子中红球的个数为（ ）A、36 B、48 C、70 D、846. 在一个不透明的袋中装有仅颜色不同的白球和红球共20个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球，记下颜色后再放回袋中；然后重复上述步骤……如表是实验中记录的部分统计数据：摸球次数
10
40
80
200
500
800
摸到红球次数
3
16
20
40
100
160
摸到红球的频率
0.3
0.4
0.25
0.2
0.2
0.2
则袋中的红球个数可能有（ ）
A、16个 B、8个 C、4个 D、2个7. 在一个不透明的袋中装有6个只有颜色不同的球，其中2个红球、1个黄球和3个白球，从袋中任意摸出一个球，是白球的概率为（ ）．A、 B、 C、 D、8. 一个不透明布袋里装有1个白球、2个黑球、3个红球，它们除颜色外均相同，从中任意摸出一个球，则是红球的可能性为（ ）A、 B、 C、 D、9. 不透明的袋子里有50张2022年北京冬奥会宣传卡片，卡片上印有会徽、吉祥物冰墩墩、吉祥物雪容融图案，每张卡片只有一种图案除图案不同外其余均相同，其中印有冰墩墩的卡片共有张.从中随机摸出1张卡片，若印有冰墩墩图案的概率是 ， 则的值是（ ）A、250 B、10 C、5 D、110. 如图A是某公园的进口，B，C，D是三个不同的出口，小明从A处进入公园，那么从B，C，D三个出口中恰好在C出口出来的概率为（ ）
A、 B、 C、 D、二、填空题
-
11. 一只不透明的袋子中装有3个红球，2个白球和1个蓝球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，则摸到球的可能性最大（填球的颜色）.12. 林业部门要观察某种树苗在一定条件下的移植成活率，下表是这种树苗在移植过程中的一组数据：
移植的棵数n
1000
1500
2500
4000
8000
15000
20000
30000
成活的棵数m
853
1356
2220
3500
7056
13170
17580
26400
成活的频率
0.853
0.904
0.888
0.875
0.882
0.878
0.879
0.880
根据以上数据，该林业部门估计在此条件下移植的55000棵树苗成活的棵数约为 ．
13. 在一个不透明的布袋中装有红球、白球共50个，这些球除颜色外都相同.小明从中随机摸出一个球记下颜色并放回，通过大量重复试验，发现摸到红球的频率稳定在0.7，则布袋中红球的个数大约是.14. 一个不透明的口袋中有红桃扑克牌与黑桃扑克牌共20张，它们除花色外都相同，将口袋中的扑克牌搅拌均匀，从中随机摸出一张，记下花色后再放回口袋中，不断重复这一过程，实验共摸了50次，发现有20次摸到的是红桃扑克牌，则这个口袋中大约有张红桃扑克牌．15. 2022年冬奥会的主题口号是“一起向未来”，从5张上面分别写着“一”“起”“向”“未”“来”这5个字的卡片（大小，形状完全相同）中随机抽取一张，则这张卡片上面恰好写着“来”字的概率是 ．三、解答题
-
16. 2017年某校初中三个年级在校学生共796名，学生的出生月份统计如下，根据图中数据回答以下问题：
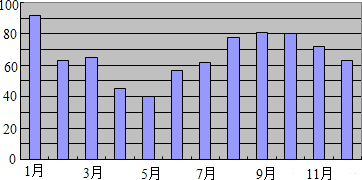(1)、出生人数少于60人的月份有哪些？(2)、至少有两个人生日在10月5日是不可能事件，还是可能事件，还是必然事件？17. 一张写有密码的纸片被随意地埋在如图所示的矩形区域内，图中的四个正方形大小一样，则纸片埋在几号区域的可能性最大?为什么?
18. 甲班56人，其中身高在160厘米以上的男同学10人，身高在160厘米以上的女同学3人，乙班80人，其中身高在160厘米以上的男同学20人，身高在160厘米以上的女同学8人．如果想在两个班的160厘米以上的女生中抽出一个作为旗手，在哪个班成功的机会大？为什么？19.将下面事件的字母写在最能代表它的概率的点上．
A：投掷一枚硬币时，得到一个正面；B：在一小时内，你步行可以走80千米；
C：给你一个骰子中，你掷出一个3；D：明天太阳会升起来．
20.在一次促销活动中，某商场为了吸引顾客，设立了一个可以自由转动的转盘（如图，转盘被平均分成16份），并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得50元、30元、20元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接获得购物券10元．
（1）求每转动一次转盘所获购物券金额的平均数；
（2）如果你在该商场消费125元，你会选择转转盘还是直接获得购物券？说明理由．
21. 小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏(扑克牌有四种花色，每种花色有13张)；小明从中任意抽取一张牌(不放回)，小颖从剩余的牌中任意抽取一张，谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为：2，3，4，5，6，7，8，9，10，J ， Q ， K ， A ， 且牌面的大小与花色无关).然后两人把摸到的牌都放回，重新开始游戏·(1)、若小明已经摸到的牌面为2，则小明获胜的概率为 ， 小颖获胜的概率为。(2)、若小明已经摸到的牌面为5，然后小颖摸牌，那么小明和小颖获胜的概率分别是多少?