（北师大版）2021-2022学年度第二学期七年级数学6.2频率的稳定性 期末复习测试卷
试卷更新日期：2022-06-06 类型：复习试卷
一、单选题
-
1. 某数学兴趣小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如图所示的统计图，那么符合这一结果的实验最有可能的是（）
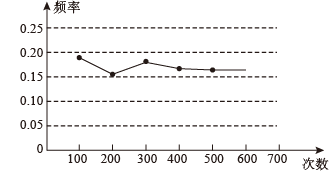A、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” B、一副只有四种花色的52张普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 C、抛掷一个质地均匀的正六面体骰子，向上的面点数是4 D、暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球2. 下列说法正确的是（ ）A、367人中至少有2人生日相同 B、任意掷一枚均匀的骰子，掷出的点数是偶数的概率是 C、天气预报说明天的降水概率为90%，则明天一定会下雨 D、某种彩票中奖的概率是1%，则买100张彩票一定有1张中3. 下表记录了一名球员在罚球线上投篮的结果．投篮次数n
50
100
150
200
250
300
500
1000
投中次数m
28
60
78
104
123
152
251
502
投中频率（精确到0.01）
0.56
0.60
0.52
0.52
0.49
0.51
0.50
0.50
由此估计这名球员在罚球线上投中篮的概率约是（ ）（精确到0.01）
A、0.50 B、0.51 C、0.49 D、0.524. 天气预报称，明天芜湖市全市的降水率为 ， 下列理解正确的是（ ）．A、明天芜湖市全市下雨的可能性较大 B、明天芜湖市全市有的地方会下雨 C、明天芜湖市全天有的时间会下雨 D、明天芜湖市一定会下雨5. 抛掷一枚质地均匀的硬币时，正面向上的概率是0.5．则下列判断正确的是（ ）A、连续掷2次时，正面朝上一定会出现1次 B、连续掷100次时，正面朝上一定会出现50次 C、连续掷次时，正面朝上一定会出现次 D、当抛掷次数越大时，正面朝上的频率越稳定于0.56. 在一个不透明的盒子中有20个除颜色外均相同的小球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.5，由此可估计袋中红球的个数为（ ）A、12个 B、10个 C、8个 D、6个7. 在一个不透明的口袋中装有4个红球和若干个白球，他们除颜色外其他完全相同．通过多次摸球试验后发现，摸到红球的频率稳定在25%附近，则口袋中白球可能有（ ）A、12个 B、14个 C、16个 D、18个8. 下表记录了一名球员在罚球线上投篮的结果：投篮次数
50
100
150
200
250
400
500
800
投中次数
28
63
87
122
148
242
301
480
投中频率
0.560
0.630
0.580
0.610
0.592
0.605
0.602
0.600
根据频率的稳定性，估计这名球员投篮一次投中的概率约是（ ）
A、0.560 B、0.580 C、0.600 D、0.6209. 投掷一枚质地均匀的硬币m次，正面向上n次，下列表达正确的是（ ）A、的值一定是 B、的值一定不是 C、m越大，的值越接近 D、随着m的增加，的值会在附近摆动，呈现出一定的稳定性10. 在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明每次摸一个后放回再摸，通过多次试验发现，摸出红球的频率稳定在左右，则袋子中红球的个数最有可能是（ ）A、8 B、5 C、12 D、15二、填空题
-
11. 某园林绿化管理局为了考察树苗的成活率，于是进行了现场统计，表中记录了树苗的成活情况，则由此估计这种树苗成活的概率约为（结果精确到0.1）．
植树总数n
400
3500
7000
9000
14000
成活数m
369
3203
6335
8073
12628
成活的频率
0.923
0.915
0.905
0.897
0.902
12. 一口袋中装有10个红球和若干个黄球（这些球除颜色外都相同），通过大量重复实验得知，摸到红球的频率为0.4.据此估计：口袋中约有个黄球.13. 一个不透明的盒子中装有8个白球和若干个红球，它们除颜色不同外，其余均相同，从盒子中随机摸出一球记下其颜色，再把它放回盒子中摇匀，重复上述过程，共试验1000次，其中有199次摸到红球，由此估计盒子中的红球大约有个．14. 小红利用计算机模拟“投针试验”：在一个平面上画一组间距为cm的平行线，将一根长度为cm的针任意投掷在这个平面上，针可能与某一直线相交，也可能与任一直线都不相交．下图显示了小红某次实验的结果，那么可以估计出针与直线相交的概率是（结果保留小数点后两位）．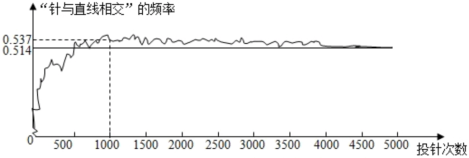
15. 社团课上，同学们进行了“摸球游戏”：在一个不透明的盒子里，装有20个除颜色不同外其余均相同的黑、白两种球，将盒子里面的球搅匀后，从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程．整理数据后，制作了“摸出黑球的频率”与“摸球的总次数”的关系图象，如图所示，经分析可以推断“摸出黑球”的概率约为 ．
三、解答题
-
16. 一个不透明的袋子中，装有1个红球，1个绿球，n个白球，这些球除颜色外都相同．搅匀后，从袋中随机摸出一个球，记录其颜色后放回；搅匀后，再从袋中随机摸出一个球，记录其颜色后放回，…，经过大量重复该试验，发现摸到绿球的频率值稳定于0.2，求n的值．17. 一个口袋中放有16个球，其中红球6个，白球和黑球各若干个，每个球除了颜色外没有任何区别.小明通过大量反复的试验（每次将球搅匀后，任意摸出一个球记下颜色后再放回）发现，取出黑球的频率稳定在 附近，请你估计袋中白球的个数18. 某封闭的纸箱中有红色、黄色的玻璃球若干，为了估计出纸箱中红色、黄色球的数目，小亮向纸箱中放入25个白球，通过多次摸球实验后，发现摸到白球的频率为25％，摸到黄球的频率为40％，试估计出原纸箱中红球、黄球的数目．
19. 下面给大家介绍密码破译的知识：密码破译本质上是一个寻找偶然事情规律的一种游戏．为了简明，我们以英语例子加以说明．
如果要传递的消息是用英语写的，你可以随意地用两个数字来代替英语中的一个字母，比如为叙述方便，用00，01，02，…25来代替26个英文字母，而每个单词之间用26隔开．当接到这样编排密码时首先要对所有的数码在密码中出现的次数进行统计，算出每个数码出现的频率．再逐步分析出每个数码代表的是哪个字母，弄清了这个问题，密码也就能破译出来了．假如你收到的密码中有一段是：
070015152426130422262404001726191426241420
你能破译出这段密码吗？
20. 南校区本学期对初三学生体育选考项目---引体向上（仅男生项目）进行抽样调查，已知完成15个可以拿到100分，完成23个为最高120分，A表示学生做引体向上23个或以上，B表示做15-22个，C表示做10-14个，D表示做9个或9个以下.根据调查结果绘制了不完整的统计图.成绩
频数（人数）
频率
A
28
x
B
14
0.2
C
m
0.3
D
n
y
(1)、抽样学生数为人，x= ， y=；(2)、补全条形统计图；(3)、若南校区初三共有720名学生，男女比例为7：5，请估计一共有多少学生可以拿到100分及以上？21. 在一个不透明的口袋里装有只有颜色不同的黑，白两种颜色的球共20只．某学习小组做摸球实验，将球搅匀后从中摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
601
摸到白球的频率m/n
0.58
0.64
0.59
0.605
0.601
（1）请填出表中所缺的数据；
（2）请估计：当n很大时，摸到白球的频率将会接近多少 （精确到0.01）
（3）请据此推断袋中白球约有多少 只．
22. 下表记录了一名球员在罚球线上投篮的结果，投篮次数（n）
50
100
150
209
250
300
350
投中次数（m）
28
60
78
104
123
152
175
投中频率（n/m）
0.56
0.60
0.52
0.50
0.49
0.51
0.58
（1）计算并填写表中的投中频率（精确到0.01）；
（2）这名球员投篮一次，投中的概率约是多少（精确到0.1）？
23. “2015扬州鉴真国际半程马拉松”的赛事共有三项：A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”．小明参加了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．（1）小明被分配到“迷你马拉松”项目组的概率．
（2）为估算本次赛事参加“迷你马拉松”的人数，小明对部分参赛选手作如下调查：
调查总人数
50
100
200
500
1000
参加“迷你马拉松”人数
21
45
79
200
401
参加“迷你马拉松”频率
0.360
0.450
0.395
0.400
0.401
①请估算本次赛事参加“迷你马拉松”人数的概率 ．（精确到0.1）
②若本次参赛选手大约有30000人，请你估计参加“迷你马拉松”的人数是多少？