(北师大版)2021-2022学年度第二学期七年级数学第五章生活中的轴对称 期末复习测试卷
试卷更新日期:2022-06-06 类型:复习试卷
一、单选题
-
1. 下列图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为( )
2. 如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为( ) A、68° B、34° C、56° D、不能确定3. 将一张细条的长方形纸条按如图方式折叠,始终使得边AB∥CD,则下列关于翻折角∠1与∠2的判断正确的是( )
A、68° B、34° C、56° D、不能确定3. 将一张细条的长方形纸条按如图方式折叠,始终使得边AB∥CD,则下列关于翻折角∠1与∠2的判断正确的是( ) A、∠1=∠2 B、∠1=2∠2 C、无论怎么折叠,∠1与∠2不可能相等 D、若∠1=50°,则∠2=40°4. 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=30°,则的度数为( )
A、∠1=∠2 B、∠1=2∠2 C、无论怎么折叠,∠1与∠2不可能相等 D、若∠1=50°,则∠2=40°4. 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=30°,则的度数为( )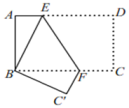 A、120° B、100° C、150° D、90°5. 有一张矩形纸片 , , , 将纸片折叠使边落在边上,折痕为 , 再将以为折痕向右折叠,与交于点(如下图),则的长为( )
A、120° B、100° C、150° D、90°5. 有一张矩形纸片 , , , 将纸片折叠使边落在边上,折痕为 , 再将以为折痕向右折叠,与交于点(如下图),则的长为( )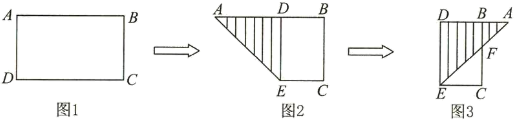 A、0.5 B、0.75 C、1 D、1.256. 如图,在Rt△ABC中, , , PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧相交于点F;③作射线AF.若AF与PQ的夹角为 , 则的度数为( )
A、0.5 B、0.75 C、1 D、1.256. 如图,在Rt△ABC中, , , PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧相交于点F;③作射线AF.若AF与PQ的夹角为 , 则的度数为( )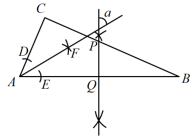 A、50° B、55° C、45° D、60°7. 如图,在等腰中, , , BD是的角平分线,则的度数等于( )
A、50° B、55° C、45° D、60°7. 如图,在等腰中, , , BD是的角平分线,则的度数等于( ) A、 B、 C、 D、8. 如图,在中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若的周长为17, , 则的周长为( )
A、 B、 C、 D、8. 如图,在中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若的周长为17, , 则的周长为( ) A、8 B、9 C、10 D、119. 如图,在2×4 的网格图中, ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 ABC成轴对称的格点三角形一共有( )
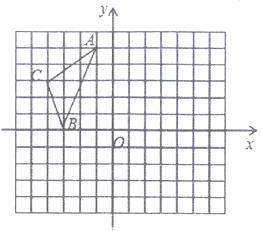
A、8 B、9 C、10 D、119. 如图,在2×4 的网格图中, ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 ABC成轴对称的格点三角形一共有( ) A、1个 B、2个 C、3个 D、4个10. 在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC关于某条直线对称的格点三角形,最多能画( )个.
A、1个 B、2个 C、3个 D、4个10. 在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC关于某条直线对称的格点三角形,最多能画( )个.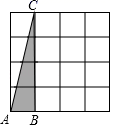 A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
11. 如图1所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示.小明按如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用10个这样的图形拼出来的图形的总长度是(结果用含a、b的代数式表示).
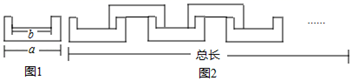 12. 如图,已知在中, , , , D是边 上一点,将沿直线AD翻折,点C落在点处,如果 , 那么点E与点B的距离等于 .
12. 如图,已知在中, , , , D是边 上一点,将沿直线AD翻折,点C落在点处,如果 , 那么点E与点B的距离等于 . 13. 如图所示,在矩形纸片ABCD中,点M是对角线AC的中点,点E是AB上一点,把△DEC沿直线DE折叠,得△DEF,点F恰好落在射线CA上.若MF=AB,则∠DAF=°.
13. 如图所示,在矩形纸片ABCD中,点M是对角线AC的中点,点E是AB上一点,把△DEC沿直线DE折叠,得△DEF,点F恰好落在射线CA上.若MF=AB,则∠DAF=°. 14. 在中, , 作AB的垂直平分线交AB于点D,交直线AC于点E,若 , 则∠B的度数为 .15. 如图,在4×4的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有个.
14. 在中, , 作AB的垂直平分线交AB于点D,交直线AC于点E,若 , 则∠B的度数为 .15. 如图,在4×4的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有个.
三、解答题
-
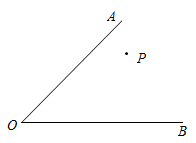
16. 如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入哪一个球袋?说明理由.
 17. 如图,把一张长方形纸片()沿折叠后,点 , 分别落在点 , 的位置上,交于点 , 若 , 求与的度数.
17. 如图,把一张长方形纸片()沿折叠后,点 , 分别落在点 , 的位置上,交于点 , 若 , 求与的度数. 18. 如图1,将矩形 沿 折叠,使顶点 落在 上的点 处,然后将矩形展平.如图2,将矩形 沿 折叠,使顶点 落在折痕 上的点 处,再将矩形 沿 折叠,此时顶点 恰好落在 上的点 处.
18. 如图1,将矩形 沿 折叠,使顶点 落在 上的点 处,然后将矩形展平.如图2,将矩形 沿 折叠,使顶点 落在折痕 上的点 处,再将矩形 沿 折叠,此时顶点 恰好落在 上的点 处.
求证:
19. 如图,四边形 中, , ,点 , 分别在 , 上,将 沿 翻折,得 ,若 , ,求 的度数. 20. 如图,中,CD平分 , 且E为AB的中点,于M,于N,请你判断线段BM与AN的数量关系并加以证明.
20. 如图,中,CD平分 , 且E为AB的中点,于M,于N,请你判断线段BM与AN的数量关系并加以证明.