(北师大版)2021-2022学年度第二学期七年级数学5.4利用轴对称进行设计 期末复习测试卷
试卷更新日期:2022-06-06 类型:复习试卷
一、单选题
-
1. 如图,在 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( )
 A、4种 B、5种 C、6种 D、7种2. 如图是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内沿直线隔着棋子对称跳行,跳行一次称为一步.已知点A为已方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为( )
A、4种 B、5种 C、6种 D、7种2. 如图是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内沿直线隔着棋子对称跳行,跳行一次称为一步.已知点A为已方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为( )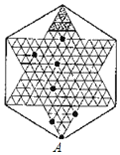 A、2 步 B、3 步 C、4 步 D、5 步3. 如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.
A、2 步 B、3 步 C、4 步 D、5 步3. 如图,是一个 3×4 的网格(由 12 个小正方形组成,虚线交点称之格点)图中有一个三角形,三个顶点都在格点上,在网格中可以画出( )个与此三角形关于某直线对称的格点三角形.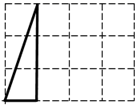 A、6 B、7 C、8 D、94. 如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有( )
A、6 B、7 C、8 D、94. 如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有( ) A、1个 B、2个 C、3个 D、4个5. 如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )
A、1个 B、2个 C、3个 D、4个5. 如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( ) A、1号袋 B、2号袋 C、3号袋 D、4号袋6. 如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A、1号袋 B、2号袋 C、3号袋 D、4号袋6. 如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( ) A、2条 B、4条 C、6条 D、8条7. 如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A、2条 B、4条 C、6条 D、8条7. 如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )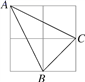 A、1个 B、3个 C、2个 D、4个8. 如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A、1个 B、3个 C、2个 D、4个8. 如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )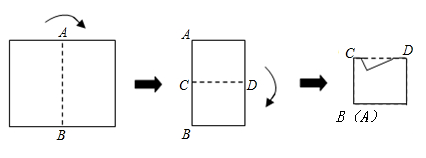 A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,在正方形网格中有两个小正方形被涂黑,再涂黑一个图中其余的小正方形,使得整个图形构成一个轴对称图形,那么涂法共有( )
9. 如图,在正方形网格中有两个小正方形被涂黑,再涂黑一个图中其余的小正方形,使得整个图形构成一个轴对称图形,那么涂法共有( ) A、2种 B、3种 C、4种 D、5种10. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、
A、2种 B、3种 C、4种 D、5种10. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、 B、
B、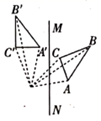 C、
C、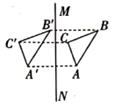 D、
D、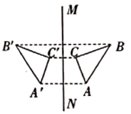
二、填空题
-
11. 如图,在 的正方形网格中,选取13个格点,以其中的三个格点A,B,C为顶点画 ,请你在图中以选取的格点为顶点再画出一个 ,使 与 成轴对称.这样的P点有个.(填P点的个数)
 12. “皮克定理”是用来计算顶点在格点(即图中虚线的交点,如图中的小黑点)上的多边形的面积公式,公式为S = a + -1.小明只记得公式中的表示多边形的面积,a 和 b 中有一个表示多边形边上(含多边形顶点)的格点个数,另一个表示多边形内部的格点个数,但记不清楚究竟是哪一个表示多边形内部的格点个数,请你利用图 1 探究并运用探究的结果求图 2 中多边形的面积是.
12. “皮克定理”是用来计算顶点在格点(即图中虚线的交点,如图中的小黑点)上的多边形的面积公式,公式为S = a + -1.小明只记得公式中的表示多边形的面积,a 和 b 中有一个表示多边形边上(含多边形顶点)的格点个数,另一个表示多边形内部的格点个数,但记不清楚究竟是哪一个表示多边形内部的格点个数,请你利用图 1 探究并运用探究的结果求图 2 中多边形的面积是.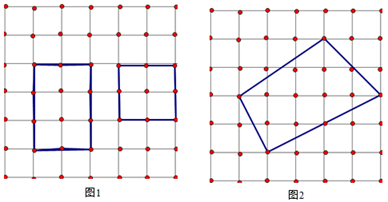 13. 如图 4×5 的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有种.
13. 如图 4×5 的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有种. 14. 如图,点P是∠AOB内部的一点,∠AOB=30°,OP=8cm,M,N是OA,OB上的两个动点,则△MPN周长的最小值cm.
14. 如图,点P是∠AOB内部的一点,∠AOB=30°,OP=8cm,M,N是OA,OB上的两个动点,则△MPN周长的最小值cm.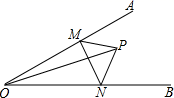 15. 如图是由三个小正方形组成的图形请你在图中补画一个小正方形使补画后的图形为轴对称图形,共有种补法.
15. 如图是由三个小正方形组成的图形请你在图中补画一个小正方形使补画后的图形为轴对称图形,共有种补法.
三、解答题
-
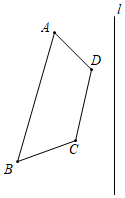
16. 如图,已知四边形ABCD和直线l,求作四边形ABCD以直线l为对称轴的对称图形A1B1C1D1 .
 17. 尺规作图:作点A关于直线l的对称点A'.
17. 尺规作图:作点A关于直线l的对称点A'.已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'. 点A'就是所求作的对称点.
由步骤①,得
由步骤②,得
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由.

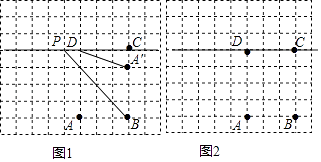
 18. 如图,有两个 7×4 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
18. 如图,有两个 7×4 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求: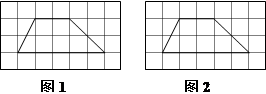
①线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
②将梯形分成两个图形,其中一个是轴对称图形;
③图1、图2中分成的轴对称图形不全等.
19. 如图,小河边有两个村庄A、B.要在河边建一自来水厂向A村与B村供水. (1)、若要使水厂到A、B村的距离相等,则应选择在哪建厂?(2)、若要使水厂到A、B村的水管最省料,应建在什么地方?20. 利用关于坐标轴对称的点的坐标的特点,在下面坐标系中作出△ABC关于y轴对称的图形△A′B′C′,并直接写出A′,B′,C′的坐标.
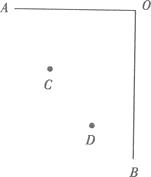
(1)、若要使水厂到A、B村的距离相等,则应选择在哪建厂?(2)、若要使水厂到A、B村的水管最省料,应建在什么地方?20. 利用关于坐标轴对称的点的坐标的特点,在下面坐标系中作出△ABC关于y轴对称的图形△A′B′C′,并直接写出A′,B′,C′的坐标.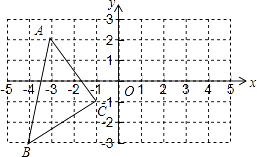 21. 某班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子。BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到空座位D上.请你帮助他设计一条行走路线,使其所走的总路程最短?
21. 某班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子。BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到空座位D上.请你帮助他设计一条行走路线,使其所走的总路程最短?