(北师大版)2021-2022学年度第二学期七年级数学4.5利用三角形全等测距离 期末复习测试卷
试卷更新日期:2022-06-06 类型:复习试卷
一、单选题
-
1. 如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )
 A、 B、 C、 D、2. 如图,点C在线段BD上,AB⊥BD于B,ED⊥BD于D.∠ACE=90°,且AC=5cm,CE=6cm,点P以2cm/s的速度沿A→C→E向终点E运动,同时点Q以3cm/s的速度从E开始,在线段EC上往返运动(即沿E→C→E→C→…运动),当点P到达终点时,P,Q同时停止运动.过P,Q分别作BD的垂线,垂足为M,N.设运动时间为t s,当以P,C,M为顶点的三角形与△QCN全等时,t的值为( )
A、 B、 C、 D、2. 如图,点C在线段BD上,AB⊥BD于B,ED⊥BD于D.∠ACE=90°,且AC=5cm,CE=6cm,点P以2cm/s的速度沿A→C→E向终点E运动,同时点Q以3cm/s的速度从E开始,在线段EC上往返运动(即沿E→C→E→C→…运动),当点P到达终点时,P,Q同时停止运动.过P,Q分别作BD的垂线,垂足为M,N.设运动时间为t s,当以P,C,M为顶点的三角形与△QCN全等时,t的值为( ) A、1或3 B、1或 C、1或 或 D、1或 或53. 如图,在测量一个小口圆形容器的壁厚时,李师傅用“X型转动钳”按如图方法进行测量,其中O是AD、CB的中点,由三角形全等的知识可知只要测量A、B的距离,即得C、D的距离,便能计算出圆形容器的壁厚.请问李师傅得到△AOB≌△COD的依据是( )
A、1或3 B、1或 C、1或 或 D、1或 或53. 如图,在测量一个小口圆形容器的壁厚时,李师傅用“X型转动钳”按如图方法进行测量,其中O是AD、CB的中点,由三角形全等的知识可知只要测量A、B的距离,即得C、D的距离,便能计算出圆形容器的壁厚.请问李师傅得到△AOB≌△COD的依据是( ) A、SAS B、SSS C、ASA D、HL4. 根据下列已知条件,能作出唯一△ABC的是( )A、AB=3,BC=4,CA=8 B、AB=4,BC=3,∠A=60° C、∠A=60°,∠B=45°,AB=4 D、∠C=90°,∠B=30°,∠A=60°5. 如图,将△ABC绕点A逆时针旋转得到 ,点C的对应点为点 , 的延长线交BC于点D , 连接AD . 则下列说法错误的是( )
A、SAS B、SSS C、ASA D、HL4. 根据下列已知条件,能作出唯一△ABC的是( )A、AB=3,BC=4,CA=8 B、AB=4,BC=3,∠A=60° C、∠A=60°,∠B=45°,AB=4 D、∠C=90°,∠B=30°,∠A=60°5. 如图,将△ABC绕点A逆时针旋转得到 ,点C的对应点为点 , 的延长线交BC于点D , 连接AD . 则下列说法错误的是( ) A、 B、 C、 D、AD平分6. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚可以放进一个等腰直角三角板(AC=BC , ∠ACB=90°)点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为( )
A、 B、 C、 D、AD平分6. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚可以放进一个等腰直角三角板(AC=BC , ∠ACB=90°)点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为( ) A、10cm B、14cm C、20cm D、6cm7. 如图,要测量河两岸相对的两点A,B的距离,先在 的垂线 上取两点C,D,使 ,再作出 的垂线 ,使点A,C,E在同一条直线上,可以说明 ,得 ,因此测得 的长就是 的长,判定 ,最恰当的理由是( )
A、10cm B、14cm C、20cm D、6cm7. 如图,要测量河两岸相对的两点A,B的距离,先在 的垂线 上取两点C,D,使 ,再作出 的垂线 ,使点A,C,E在同一条直线上,可以说明 ,得 ,因此测得 的长就是 的长,判定 ,最恰当的理由是( ) A、 B、 C、 D、8. 如图,点 、 分别在正方形 的边 、 上, ,已知 (正方形的四条边都相等,四个内角都是直角), .则 的面积 ( )
A、 B、 C、 D、8. 如图,点 、 分别在正方形 的边 、 上, ,已知 (正方形的四条边都相等,四个内角都是直角), .则 的面积 ( ) A、6 B、12 C、15 D、309. 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使 ,连接BC并延长到点E,使 ,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到 ,理由是( )
A、6 B、12 C、15 D、309. 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使 ,连接BC并延长到点E,使 ,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到 ,理由是( ) A、SSS B、AAS C、ASA D、SAS10. 如图,在 中, , , ,则 等于( )
A、SSS B、AAS C、ASA D、SAS10. 如图,在 中, , , ,则 等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在新年联欢会上,老师设计了“你说我画”的游戏.游戏规则如下:甲同学需要根据乙同学提供的三个条件画出形状和大小都确定的三角形.已知乙同学说出的前两个条件是“ , ”.现仅存下列三个条件:①;②;③ . 为了甲同学画出形状和大小都确定的 , 乙同学可以选择的条件有: . (填写序号,写出所有正确答案)12. 如图, , , , 则、两点之间的距离为 .
 13. 如图,要测量水池宽AB , 可从点A出发在地面上画一条线段AC , 使AC⊥AB , 再从点C观测,在BA的延长线上测得一点D , 使∠ACD=∠ACB , 这时量得AD=110m , 则水池宽AB的长度是m .
13. 如图,要测量水池宽AB , 可从点A出发在地面上画一条线段AC , 使AC⊥AB , 再从点C观测,在BA的延长线上测得一点D , 使∠ACD=∠ACB , 这时量得AD=110m , 则水池宽AB的长度是m . 14. 如图,方格中有四个相同的正方形,则∠1,∠2,∠3的度数之和是 .
14. 如图,方格中有四个相同的正方形,则∠1,∠2,∠3的度数之和是 .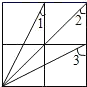 15. 如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作DE⊥BD交AC的延长线于点E,垂足为点D,测得ED=3,CD=4,则A、B两点间的距离等于.
15. 如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作DE⊥BD交AC的延长线于点E,垂足为点D,测得ED=3,CD=4,则A、B两点间的距离等于.
三、解答题
-
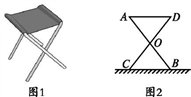
16. 如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
 17. 如图所示,为方便游客观赏的需要,需要在人工湖两侧A , B两点之间修建一条观光步道,但无法直接量出A , B两点之间的距离,现在有一足够长的米尺,请你利用所学数学知识,设计一种方案,大致测出A , B两点之间的距离,并说明理由.
17. 如图所示,为方便游客观赏的需要,需要在人工湖两侧A , B两点之间修建一条观光步道,但无法直接量出A , B两点之间的距离,现在有一足够长的米尺,请你利用所学数学知识,设计一种方案,大致测出A , B两点之间的距离,并说明理由. 18. 如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使 过点D作 ,且A,C,E三点在一直线上.若测得 米,即可知道AB也为15米.请说明理由.
18. 如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D,使 过点D作 ,且A,C,E三点在一直线上.若测得 米,即可知道AB也为15米.请说明理由. 19. 如图,小强学习全等三角形后,用10块高度都是5cm的相同长方体积木,搭了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
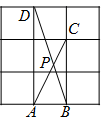
19. 如图,小强学习全等三角形后,用10块高度都是5cm的相同长方体积木,搭了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离. 20. 沛沛沿一段笔直的人行道行走,边走边欣赏风景,在由 走到 的过程中,通过隔离带的空隙 ,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图, ,相邻两平行线间的距离相等 , 相交于 , 垂足为 .已知 米.请根据上述信息求标语 的长度.
20. 沛沛沿一段笔直的人行道行走,边走边欣赏风景,在由 走到 的过程中,通过隔离带的空隙 ,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图, ,相邻两平行线间的距离相等 , 相交于 , 垂足为 .已知 米.请根据上述信息求标语 的长度. 21. 公路上,A,B两站相距 千米,C、D为两所学校, 于点A, 于点B,如图,已知 千米,现在要在公路 上建一报亭H,使得C、D两所学校到H的距离相等,且 ,问:H应建在距离A站多远处?学校C到公路的距离是多少千米?
21. 公路上,A,B两站相距 千米,C、D为两所学校, 于点A, 于点B,如图,已知 千米,现在要在公路 上建一报亭H,使得C、D两所学校到H的距离相等,且 ,问:H应建在距离A站多远处?学校C到公路的距离是多少千米?