(北师大版)2021-2022学年度第二学期七年级数学4.3探索三角形全等的条件 期末复习测试卷
试卷更新日期:2022-06-06 类型:复习试卷
一、单选题
-
1. 如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若 , . 则AB的长可能是( )
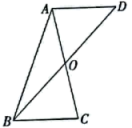 A、3 B、4 C、7 D、112. 如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下:
A、3 B、4 C、7 D、112. 如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下: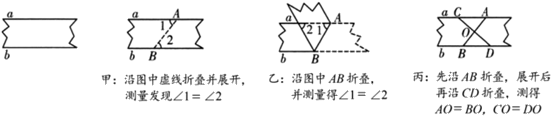
下列判断正确的是( )
A、甲、乙能得到 , 丙不能 B、甲、丙能得到 , 乙不能 C、乙、丙能得到 , 甲不能 D、甲、乙、丙均能得到3. 判断两个直角三角形全等的方法错误的有( )A、两条直角边对应相等 B、斜边和一锐角对应相等 C、斜边和一条直角边对应相等 D、两个锐角对应相等4. 如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是( ) A、两点之间线段最短 B、三角形具有稳定性 C、经过两点有且只有一条直线 D、垂线段最短5. 如图所示,EF过矩形ABCD对角线的交点O,且分别交AD,BC于点E,F.已知AB=3,BC=4,则图中阴影部分的面积是( )
A、两点之间线段最短 B、三角形具有稳定性 C、经过两点有且只有一条直线 D、垂线段最短5. 如图所示,EF过矩形ABCD对角线的交点O,且分别交AD,BC于点E,F.已知AB=3,BC=4,则图中阴影部分的面积是( ) A、3 B、4 C、6 D、126. 如图, ,要使 .则添加的一个条件不能是( )
A、3 B、4 C、6 D、126. 如图, ,要使 .则添加的一个条件不能是( ) A、 B、 C、 D、7. 在△ABC和△DEF中,已知 BC=EF ,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )A、AC = DF B、AB = DE C、∠A=∠D D、∠B=∠E8. 如图,已知 ,添加下列条件中的一个,不能判断 的是( )
A、 B、 C、 D、7. 在△ABC和△DEF中,已知 BC=EF ,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )A、AC = DF B、AB = DE C、∠A=∠D D、∠B=∠E8. 如图,已知 ,添加下列条件中的一个,不能判断 的是( )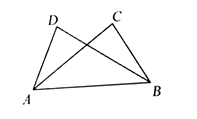 A、 B、 C、 D、9. 根据下列条件,不能画出唯一确定的△ABC的是( )A、AB=3,BC=4,AC=6 B、AB=4,∠B=45°,∠A=60° C、AB=4,BC=3,∠A=30° D、∠C=90°,AB=8,AC=410. 如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是( )
A、 B、 C、 D、9. 根据下列条件,不能画出唯一确定的△ABC的是( )A、AB=3,BC=4,AC=6 B、AB=4,∠B=45°,∠A=60° C、AB=4,BC=3,∠A=30° D、∠C=90°,AB=8,AC=410. 如图,在△ABC和△DEF中,∠C=∠F=90°,添加下列条件,不能判定这两个三角形全等的是( ) A、∠A=∠D,∠B=∠E B、AC=DF,AB=DE C、∠A=∠D,AB=DE D、AC=DF,CB=FE
A、∠A=∠D,∠B=∠E B、AC=DF,AB=DE C、∠A=∠D,AB=DE D、AC=DF,CB=FE二、填空题
-
11. 如图,点P在直线 外,点A、B、C、D均在直线 上,如果 ,只需添加一个条件即可证明 ,这个条件可以是(写出一个即可).
 12. 工人师傅常常利用角尺平分一个角.如图,在∠AOB的两边OA、OB上分别任取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,这时过角尺顶点P的射线OP就是∠AOB的平分线的依据是 . (选填“SSS”、“SAS”、“AAS”、“HL”、“ASA”)
12. 工人师傅常常利用角尺平分一个角.如图,在∠AOB的两边OA、OB上分别任取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,这时过角尺顶点P的射线OP就是∠AOB的平分线的依据是 . (选填“SSS”、“SAS”、“AAS”、“HL”、“ASA”)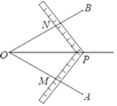 13. 如图,在△ABC中,AD⊥BC于点D,AD与BE相交于点F,且AC=BF,DF=DC.若∠ABE=10°,则∠DBF的度数为 .
13. 如图,在△ABC中,AD⊥BC于点D,AD与BE相交于点F,且AC=BF,DF=DC.若∠ABE=10°,则∠DBF的度数为 .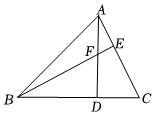 14. 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是 .
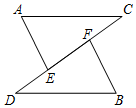
14. 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是 . 15. 如图,在四边形ABCD中,E为边AD上一点, , 且 , , , , 则AB的长度为 .
15. 如图,在四边形ABCD中,E为边AD上一点, , 且 , , , , 则AB的长度为 .
三、解答题
-
16. 如图,点E、F分别是矩形ABCD的边AB、CD上的一点,且AF=CE.求证:△ADF≌△CBE.
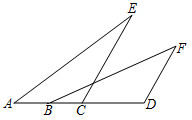
 17. 已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明.
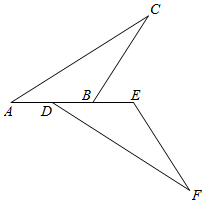
17. 已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明. 18. 如图,点A,B,C,D在同一条直线上,CE//DF,EC=BD,∠A=∠F.求证:AE=FB.
18. 如图,点A,B,C,D在同一条直线上,CE//DF,EC=BD,∠A=∠F.求证:AE=FB.