（北师大版）2021-2022学年度第二学期七年级数学2.3平行线的性质 期末复习测试卷
试卷更新日期：2022-06-05 类型：复习试卷
一、单选题
-
1. 如图，已知l1∥l2 ， l3分别与l1、l2相交，点A、B分别为l3 ， l2上一点，且AB⊥l2 ， 若∠1＝52°，则∠2的度数为（ ）
A、28° B、42° C、38° D、32°2. 如图，已知AB∥CD，则∠α、∠β和∠γ之间的关系为 （ ）
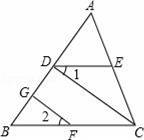
A、β＋γ－α＝180° B、α＋γ＝β C、α＋β＋γ＝360° D、α＋β－2γ＝180°3. 已知：如图AB∥CD，EF交AB于G，交CD于F，FH平分∠EFD，交AB于H，∠AGE＝50°，则∠BHF的度数为（ ）
A、115° B、65° C、50° D、130°4. 如图，在△ABC中， ． BD、CD分别平分∠ABC，∠ACB，过点D作直线平行于BC，交AB、AC于点E、F，则线段EF和BE＋CF的大小关系为（ ）
A、 B、 C、 D、不能确定5. 如图，由 ， 可以得到（ ）
A、 B、 C、 D、6. 如图，AB∥CD，BC为∠ACD的角平分线，∠1＝155°，则∠2为（ ）
A、155° B、130° C、150° D、135°7. 如图，将一副三角尺按如图所示的位置在同一平面内摆放，其中∠ACB＝∠CED＝90°，∠B＝30°，∠ECD＝45°．若 ，CB与DE相交于点F ， 则∠BCD的度数为（ ）
A、15° B、20° C、25° D、30°8. 如图，直线AB∥CD ， 点F是CD上一点，∠EFG＝90°，EF交AB于M ， 若∠CFG＝35°，则∠AME的大小为（ ）
A、35° B、55° C、125° D、130°9. 如图， ．点E在直线 上，点F在直线 上，过点E作 于E，如果 ，那么 的大小为（ ）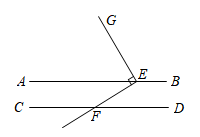
A、 B、 C、 D、10. 如图，下列推理及所注明的理由都正确的是（ ）
A、因为 ， 所以（同位角相等，两直线平行） B、因为 ， 所以（两直线平行，内错角相等） C、因为 ， 所以（两直线平行，内错角相等） D、因为 ， 所以（内错角相等，两直线平行）二、填空题
-
11. 如图，直线//直线 ， 一个含角的直角三角尺的两个锐角顶点分别落在直线、上．若 ， 则 ．
12. 将直角三角板按如图所示的位置放置， ， ， 直线// ， 平分 ， 在直线上确定一点 ， 满足 ， 则 ．
13. 已知直线 ， 把一块含30°角的直角三角板按如图方式放置，若 ， 则°．
14. 如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1=40°，则∠2的度数为 ．
15. 如图， ∥ ，点 ， 分别是 ， 上的一点，射线 绕点 顺时针旋转，速度为每秒 度，射线 绕点 顺时针旋转，速度为每秒 度，旋转至与 重合便立即回转，当射线 旋转至与 重合时， 与 都停止转动.若射线 先转动 秒，射线 才开始转动，则射线 转动秒后， 与 平行.
三、解答题
-
16. 如图，一块平面反光镜在∠AOB的边OA上，∠AOB=40°，在OB上有一点P，从P点射出一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，由科学实验知道：∠OQP=∠AQR，求∠QPB的度数．
17. 如图，已知∠1＝∠2，∠A＝29°，求∠C的度数．
18. 已知：如图，AB//CD，∠B＝∠D，求证：∠E＝∠BCA．（完成下列推理证明）
证明：∵AB∥CD（已知）
∴∠B＝∠ ▲ （两直线平行，内错角相等）
∵∠B＝∠D（已知）
∴∠D＝∠ ▲ （ ）
∴ED// ▲ （ ）
∴∠E＝∠BCA（ ）
19. 完成下面推导过程：如图，点、在直线上，点在线段上，与相交于点 ， ， ， 试判断与之间的数量关系.
∵（已知）
∴ （ ）
∴（ ）
∵（已知）
∴（等量代换）
∴ （ ）
∴（ ）
20. 如图，直线AB∥CD，直线EF与AB、CD相交于点P，与CD相交于Q，且PM⊥EF，若∠1=68°，求∠2的度数。
