(北师大版)2021-2022学年度第二学期七年级数学1.4整式的乘法 期末复习测试卷
试卷更新日期:2022-06-03 类型:复习试卷
一、单选题
-
1. 如图所示的正方形和长方形卡片各有若干张,若要拼成一个长为 ,宽为 的长方形,则需要 类, 类, 类卡片各( )张.


 A、2,3,2 B、2,4,2 C、2,5,2 D、2,5,42. 的展开式中不含xy项,则k的值是( )A、 B、 C、 D、3. 若的积中不含x的二次项和一次项,则a和b的值( )A、a=0;b=2 B、a=3;b=9 C、a=-1;b=2 D、a=2;b=44. 下列等式成立的是( )A、 B、 C、 D、5. 若等式 成立,则 的值分别为( )A、 B、 C、 D、6. 从前,古希腊一位庄园主把一块长为a米,宽为b米()的长方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的长增加10米,宽减少10米.维续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )A、变小了 B、变大了 C、没有变化 D、无法确定7. 若(x-2)(x2-mx+1)的展开式中不含x的二次项,则化简后的一次项系数是( )A、-3 B、-2 C、 D、8. 已知9x=25y=15,那么代数式(x-1)(y-1)+xy+3的值是( )A、4 B、3 C、2 D、19. 如果多项式与的乘积展开式中不含x的一次项,且常数项为6,则的值为( )A、-12 B、-6 C、6 D、1810. 如果(2x+m)(x﹣3)展开后结果中不含x的一次项,则m等于( )A、3 B、﹣6 C、﹣3 D、6
A、2,3,2 B、2,4,2 C、2,5,2 D、2,5,42. 的展开式中不含xy项,则k的值是( )A、 B、 C、 D、3. 若的积中不含x的二次项和一次项,则a和b的值( )A、a=0;b=2 B、a=3;b=9 C、a=-1;b=2 D、a=2;b=44. 下列等式成立的是( )A、 B、 C、 D、5. 若等式 成立,则 的值分别为( )A、 B、 C、 D、6. 从前,古希腊一位庄园主把一块长为a米,宽为b米()的长方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的长增加10米,宽减少10米.维续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )A、变小了 B、变大了 C、没有变化 D、无法确定7. 若(x-2)(x2-mx+1)的展开式中不含x的二次项,则化简后的一次项系数是( )A、-3 B、-2 C、 D、8. 已知9x=25y=15,那么代数式(x-1)(y-1)+xy+3的值是( )A、4 B、3 C、2 D、19. 如果多项式与的乘积展开式中不含x的一次项,且常数项为6,则的值为( )A、-12 B、-6 C、6 D、1810. 如果(2x+m)(x﹣3)展开后结果中不含x的一次项,则m等于( )A、3 B、﹣6 C、﹣3 D、6二、填空题
-
11. 2a· () .12. 若 , 则m-n.13. 如图,正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),如果要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙)、且卡片全部用上,则不同的选取方案有种.
 14. 如果 的积中不含x的一次项,则m的值是.15. 如果(x+a)(3x﹣6)的乘积中不含x的一次项,则a= .
14. 如果 的积中不含x的一次项,则m的值是.15. 如果(x+a)(3x﹣6)的乘积中不含x的一次项,则a= .三、解答题
-
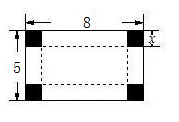
16. 如图,在长8cm,宽5cm的长方形塑料板的四个角剪去4个边长为 的小正方形,按折痕做一个无盖的长方体盒子,求盒子的容积(塑料板的厚度忽略不计).
 17. 如图,公园里有A、B两个花坛,A花坛是长为20米,宽为 米的长方形,花坛中间16横竖各铺设一条小路(阴影部分),竖着的小路宽为0.5米,横着的小路宽为1米,剩余部分栽种花卉;B花坛是直径为 米的半圆,其中修建一个半圆形水池(阴影部分),剩余部分栽种花卉,求B花坛比A花坛栽种花卉的面积大多少?(取 )
17. 如图,公园里有A、B两个花坛,A花坛是长为20米,宽为 米的长方形,花坛中间16横竖各铺设一条小路(阴影部分),竖着的小路宽为0.5米,横着的小路宽为1米,剩余部分栽种花卉;B花坛是直径为 米的半圆,其中修建一个半圆形水池(阴影部分),剩余部分栽种花卉,求B花坛比A花坛栽种花卉的面积大多少?(取 )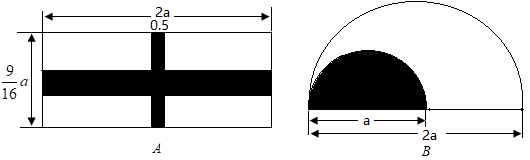 18. 已知多项式 的结果中不含 项和 项,求 和 的值.19. 阅读下列文字,并解决问题。
18. 已知多项式 的结果中不含 项和 项,求 和 的值.19. 阅读下列文字,并解决问题。已知x2y=3,求2xy(x5y2-3x3y-4x)的值.
分析:考虑到满足x2y=3的x,y的可能值较多,不可以逐一代入求解,故考虑整体思想,将x2y=3整体代入.
解:2xy(x5y2-3x3y-4x)
=2x6y3-6x4y2-8x2y
=2(x2y)3-6(x2y)2-8x2y,
将x2y=3代入
原式=2×33-6×32-8×3=-24.
请你用上述方法解决下面问题:
已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值.
20. 若 展开后不含x2、x3项,求pq的值.