浙江省舟山市新城区域2022年中考数学二模试卷

试卷更新日期：2022-06-02 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 下列四个数中，最大的数是（）

A、0 B、﹣3 C、1 D、 $\frac{1}{2}$

查看试题解析
2. 如图，是由棱长都相等的四个小正方体组成的几何体．该几何体的左视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是( )

A、x•x²=x² B、（xy）²=xy² C、（x²）³=x⁶ D、x²+x²=x⁴

查看试题解析
4. 二十四节气是中国古代劳动人民长期经验积累的结晶，它与白昼时长密切相关.当春分、秋分时，昼夜时长大致相等；当夏至时，白昼时长最长，如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过14小时的节气是（）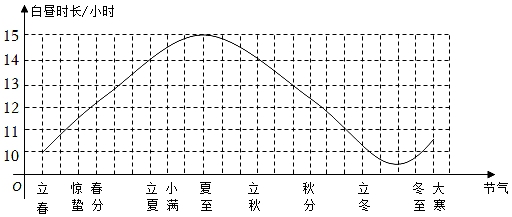

A、惊蛰 B、立夏 C、夏至 D、大寒

查看试题解析
5. 如图，BC是⊙O的直径，AD⊥BC，∠ABC＝25°，则弧CD的度数（）

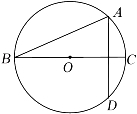A、50° B、25° C、100° D、65°

查看试题解析
6. 一个不透明布袋里装有1个白球、2个黑球、3个红球，它们除颜色外均相同．从中任意摸出一个球，则是红球的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
7. 如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A、D为圆心，以大于 $\frac{1}{2}$ AD的长为半径在AD两侧作弧，交于两点M、N；第二步，连结MN分别交AB、AC于点E、F；第三步，连接DE、DF.若BD＝8，AF＝6，CF＝3，则CD的长是（）

A、8 B、6 C、5 D、4

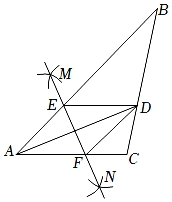查看试题解析
8. 如图，直线y $= - \frac{3}{4}$ x+5交坐标轴于点A、B，与坐标原点构成的△AOB向x轴正方向平移4个单位长度得△A′O′B′，边O′B′与直线AB交于点E，则图中阴影部分面积为（）

A、 $\frac{16}{5}$ B、15 C、10 D、14

查看试题解析
9. 如图，在矩形ABCD中，AB＝2，BC＝2 $\sqrt{5}$ ，E是BC的中点，将△ABE沿直线AE翻折，点B落在点F处，连接CF，则cos∠ECF的值为（）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{10}}{4}$ C、 $\frac{\sqrt{5}}{3}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
10. 若二次函数y＝a²x²﹣bx﹣c的图象，过不同的六点A（﹣1，n）、B（5，n﹣1）、C（6，n+1）、D（ $\sqrt{2}$ ，y₁）、E（2，y₂）、F（4，y₃），则y₁、y₂、y₃的大小关系是（　　）

A、y₁＜y₂＜y₃ B、y₁＜y₃＜y₂ C、y₂＜y₃＜y₁ D、y₂＜y₁＜y₃

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 若 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 因式分解：x²﹣4y²＝.

查看试题解析
13. 将一副含30°角和45°角的直角三角板按如图共顶点摆放，若AB∥CD，则∠CAE＝.

查看试题解析
14. 如图，矩形OABC的顶点A、C分别在x轴、y轴上，B（﹣2，1），将矩形OABC绕点O顺时针旋转，点B落在y轴上的点D处，若反比例函数 $y = \frac{k}{x}$ （x＜0）的图象经过点E，则k的值为 .

查看试题解析
15. 《九章算术》是古代东方数学代表作，书中记载：今有开门去阃（读kǔn，门槛的意思）一尺，不合二寸，问门广几何？题目大意是：如图1、2（图2为图1的平面示意图），推开双门，双门间隙CD的距离为2寸，点C和点D距离门槛AB都为1尺（1尺＝10寸），则AB的长是寸．

查看试题解析
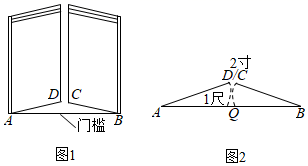16. 如图，用图1中的a张长方形和b张正方形纸板作侧面和底面，做成如图2的竖式和横式两种无盖纸盒，若a+b的值在285和315之间（不含285与315），且用完这些纸板做竖式纸盒比横式纸盒多30个，则a的值可能是 .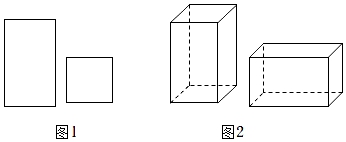

查看试题解析

三、解答题（本题共8小题，第17～19题每6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

17.

(1)、计算： $2^{0} + {(\frac{1}{2})}^{- 1} - \sqrt{9}$

(2)、化简：（a+1）²+a（2﹣a）

查看试题解析
18. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简.过程如图所示：

(1)、接力中，自己负责的一步出现错误的是

A、只有乙 B、甲和丁 C、乙和丙 D、乙和丁

(2)、请你书写正确的化简过程，并在“1，0，2，﹣2”中选择一个合适的数求值.

查看试题解析
19. 某校七年级共有500名学生，在“世界读书日”前夕，开展了“阅读助我成长”的读书活动．为了解该年级学生在此次活动中课外阅读情况，随机抽取m名学生，调查他们课外阅读书籍的数量，将收集的数据整理成如下统计表和扇形图．
学生读书数量统计表
阅读量/本
学生人数
1
15
2
a
3
b
4
5

(1)、直接写出m、a、b的值；

(2)、估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本？

查看试题解析
20. 如图，在Rt△ABC中，∠C＝90°，D是边BC上一点，连结AD并延长至点E，AD＝DE，过点E作EF⊥BC于点F，连结BE.

(1)、求证：△ADC≌△EDF.

(2)、若BE＝DE，AC＝8，CD＝4，求AB的长.

查看试题解析
21. 如图，在平面直角坐标系中，二次函数y＝ax²+4x﹣3图象的顶点是A，与x轴交于B，C两点，与y轴交于点D.点B的坐标是（1，0）.

(1)、求A，C两点的坐标，并根据图象直接写出当y＞0时x的取值范围.

(2)、将图象向上平移m个单位后，二次函数图象与x轴交于E，F两点，若EF＝6，求m的值.

查看试题解析
22. 我市的白沙岛是众多海钓人的梦想之地.小明的爸爸周末去白沙岛钓鱼，将鱼竿AB摆成如图1所示.已知AB＝4.8m，鱼竿尾端A离岸边0.4m，即AD＝0.4m.海面与地面AD平行且相距1.2m，即DH＝1.2m.

（参考数据：sin37°＝co553° $\approx \frac{3}{5}$ ，cos37°＝sin53° $\approx \frac{4}{5}$ ，tan37° $\approx \frac{3}{4}$ ，sin22° $= \frac{3}{8}$ ，cos22° $\approx \frac{15}{16}$ ，tan22° $\approx \frac{2}{5}$ ）

(1)、如图1，在无鱼上钩时，鱼竿AB与地面AD的夹角∠BAD＝22°，海面上方的鱼线BC与海面HC成一定角度.求点B到海面HC的距离；

(2)、如图2，在有鱼上钩时，鱼竿与地面的夹角∠BAD＝53°，此时鱼线被拉直，鱼线BO＝5.46m，点O恰好位于海面.求点O到岸边DH的距离.

查看试题解析
23. 我们知道：如图①，点B把线段AC分成两部分，如果 $\frac{B C}{A B} = \frac{A B}{A C}$ .那么称点为B线段AC的黄金分割点.它们的比值为 $\frac{\sqrt{5} - 1}{2}$ .

(1)、在图①中，若AC＝10cm，则AB的长为 cm；

(2)、如图②，用边长为10cm的正方形纸片进行如下操作：对折正方形ABCD得折痕EF，连接CE，将CB折叠到CE上，点B对应点H，得折痕CG.试说明G是AB的黄金分割点；

(3)、如图③，小明进一步探究：在边长为a的正方形ABCD的边AD上任取点E，连接BE，作CF⊥BE，交AB于点F，延长EF、CB交于点P.他发现当PB与BC满足某种关系时E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现，并说明理由.

查看试题解析
24. 如图，已知AC＝6cm，∠GAC＝90°，AD是∠GAC的平分线.动点N从点C出发，以1cm/s的速度沿CA水平向左作匀速运动，与此同时，动点M从点A出发，也以1cm/s的速度沿AG竖直向上作匀速运动.连接MN，交OD于点E.经过A，M，N三点作圆，交AD于点F，连接FM、FN.设运动时间为t（s），其中0＜t＜6.

(1)、用含t的代数式表示线段MN的长，并求MN的最小值.

(2)、求四边形AMFN的面积.

(3)、是否存在实数t，使得线段AE的长度最大？若存在，求出t的值；若不存在，说明理由.

查看试题解析

阅读量/本	学生人数
1	15
2	a
3	b
4	5