浙江省温州市龙湾区2022年初中学业水平考试第二次适应性测试数学试卷
试卷更新日期:2022-06-02 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分.)
-
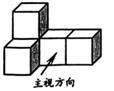
1. 计算 的结果是( )A、-6 B、-1 C、1 D、62. 金星是太阳系八大行星中距离地球最近的行星,也是人在地球上看到的最亮的一颗星,金星离地球的距离为42000000千米.数据42000000用科学记数法表示为( )A、 B、 C、 D、3. 如图的几何体由五个相同的小正方体搭成,它的俯视图是( )
 A、
A、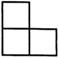 B、
B、 C、
C、 D、
D、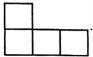 4. 在同一副扑克牌中抽取2张“黑桃”,5张“梅花”,3张“方块”.将这10张牌背面朝上,从中任意抽取1张,是“方块”的概率为( )A、 B、 C、 D、5. 若代数式 的值为8,则代数式 的值为( )A、0 B、11 C、-7 D、-156. 如图,将一块直角三角板的直角边 贴在直线 上, ,以点 为圆心,斜边 长为半径向右画弧,交直线 于点 .若 ,则 的长为( )
4. 在同一副扑克牌中抽取2张“黑桃”,5张“梅花”,3张“方块”.将这10张牌背面朝上,从中任意抽取1张,是“方块”的概率为( )A、 B、 C、 D、5. 若代数式 的值为8,则代数式 的值为( )A、0 B、11 C、-7 D、-156. 如图,将一块直角三角板的直角边 贴在直线 上, ,以点 为圆心,斜边 长为半径向右画弧,交直线 于点 .若 ,则 的长为( ) A、 B、 C、 D、7. 某气球内充满一定质量的气体,温度不变时,气球内气体的压强 与气体的体积 的关系是如图所示的反比例函数.当气球内气体的压强大于200kPa,气球就会爆炸.为了不让气球爆炸,则气球内气体的体积 需满足的取值范围是( )
A、 B、 C、 D、7. 某气球内充满一定质量的气体,温度不变时,气球内气体的压强 与气体的体积 的关系是如图所示的反比例函数.当气球内气体的压强大于200kPa,气球就会爆炸.为了不让气球爆炸,则气球内气体的体积 需满足的取值范围是( )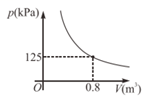 A、 B、 C、 D、8. 如图, , 是 的两条弦,且 ,点 , 分别在 , 上.若 ,则 的度数为( )
A、 B、 C、 D、8. 如图, , 是 的两条弦,且 ,点 , 分别在 , 上.若 ,则 的度数为( ) A、119° B、112° C、109° D、108°9. 若三个方程 , , 的正根分别记为 , , ,则下列判断正确的是( )A、 B、 C、 D、10. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,在 中, ,以 的各边为边分别向外作正方形,再将较小的两个正方形按图2所示放置,连结 , .若 ,且 ,则 的长为( )
A、119° B、112° C、109° D、108°9. 若三个方程 , , 的正根分别记为 , , ,则下列判断正确的是( )A、 B、 C、 D、10. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,在 中, ,以 的各边为边分别向外作正方形,再将较小的两个正方形按图2所示放置,连结 , .若 ,且 ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题5分,共30分)
-
11. 分解因式:2a2﹣8a+8= .12. 温州2022年5月1至7日气温折线统计图如图所示,由图可知,这七天中温差最大那天的温度相差 摄氏度.
 13. 一段长为 ,弧度为60°的弧所在圆的半径长为 .14. 在平面直角坐标系中,若点 在第四象限内,则 的取值范围是 .15. 如图,点 , , , 分别是矩形 各边上的中点,将矩形 向右平移得矩形 ,点 , , , 的对应点分别为点 , , , .若 ,矩形 的面积为84,则图中阴影部分的面积为 .
13. 一段长为 ,弧度为60°的弧所在圆的半径长为 .14. 在平面直角坐标系中,若点 在第四象限内,则 的取值范围是 .15. 如图,点 , , , 分别是矩形 各边上的中点,将矩形 向右平移得矩形 ,点 , , , 的对应点分别为点 , , , .若 ,矩形 的面积为84,则图中阴影部分的面积为 . 16. 如图,岸边堤坝和湖中分别伫立着甲、乙两座电线塔,甲塔底 和堤坝 段均与水平面 平行, 为 中点, 米, 米.某时刻甲塔顶
16. 如图,岸边堤坝和湖中分别伫立着甲、乙两座电线塔,甲塔底 和堤坝 段均与水平面 平行, 为 中点, 米, 米.某时刻甲塔顶 影子恰好落在斜坡底端 处,此时小章测得2米直立杆子的影长为1米.随后小章乘船行驶至湖面点 处,发现点 , , 三点共线,并在 处测得甲塔底 和乙塔顶 的仰角均为 ,则塔高 的长为米;若小章继续向右行驶10米至点 ,且在 处测得甲、乙两塔顶 , 的仰角均为 .若点 , , , 在同一水平线上, ,则甲、乙两塔顶 , 的距离为米.(参考数据: , , , )
影子恰好落在斜坡底端 处,此时小章测得2米直立杆子的影长为1米.随后小章乘船行驶至湖面点 处,发现点 , , 三点共线,并在 处测得甲塔底 和乙塔顶 的仰角均为 ,则塔高 的长为米;若小章继续向右行驶10米至点 ,且在 处测得甲、乙两塔顶 , 的仰角均为 .若点 , , , 在同一水平线上, ,则甲、乙两塔顶 , 的距离为米.(参考数据: , , , )

三、解答题(本题有8小题,共80分.)
-
17.(1)、计算: .(2)、化简: .18. 如图,在四边形 中, , , ,垂足为点 , .
 (1)、求证: .(2)、若 ,求
(1)、求证: .(2)、若 ,求 度数. 19. 某公司要招聘一名职员,面试中甲、乙、丙三名应聘者各项得分如下表:
度数. 19. 某公司要招聘一名职员,面试中甲、乙、丙三名应聘者各项得分如下表:学历
能力
态度
甲
80
87
85
乙
75
91
83
丙
90
78
87
(1)、若根据三项得分的平均分择优录取,已求甲的平均分为84分,通过计算确定谁将被录用?(2)、若该公司规定学历、能力、态度测试占总分的比例分别为20%, , .若你是这家公司的招聘者,按你认为的“重要程度”设计能力和态度两项得分在总分中的比例,并以此为依据确定谁将被录用?请简要说明这样设计的理由.20. 如图是由54个边长为1的小等边三角形组成的网格,请按要求画格点多边形(顶点均在格点上).
 (1)、在图1中画一个以 为腰的 .(2)、在图2中画一个四边形 ,使其中一条对角线长为4,且恰有两个内角为90°.21. 如图,将抛物线 平移后得到抛物线 ,两抛物线与 轴分别交于点 , .抛物线 , 的交点 的横坐标是1,过点 作 轴的平行线,分别交抛物线 , 于点 , .
(1)、在图1中画一个以 为腰的 .(2)、在图2中画一个四边形 ,使其中一条对角线长为4,且恰有两个内角为90°.21. 如图,将抛物线 平移后得到抛物线 ,两抛物线与 轴分别交于点 , .抛物线 , 的交点 的横坐标是1,过点 作 轴的平行线,分别交抛物线 , 于点 , . (1)、求抛物线 的对称轴和点 的横坐标.(2)、求线段 和 的长度.22. 如图,在 中, , .点 , 落在 上, 的延长线交 于点 ,作直径 交 于点 , 切 于点 ,交 的延长线于点 .
(1)、求抛物线 的对称轴和点 的横坐标.(2)、求线段 和 的长度.22. 如图,在 中, , .点 , 落在 上, 的延长线交 于点 ,作直径 交 于点 , 切 于点 ,交 的延长线于点 . (1)、求证:四边形 为平行四边形.(2)、若 , ,求
(1)、求证:四边形 为平行四边形.(2)、若 , ,求 长. 23. 物流行业发展迅速,为满足快递员通讯需求,某通讯公司推出三种套餐,如下表:
长. 23. 物流行业发展迅速,为满足快递员通讯需求,某通讯公司推出三种套餐,如下表:套餐
套餐
套餐
月租费(元)
79
89
119
每月免费通话时间(分)
1700
2000
优惠减免
无
每月减免20元
资费说明
国内通话超出部分按 元/分钟计费.
 (1)、 , , 三种套餐每月所需费用 (元)与每月通话时间 (分)之间的函数关系如图所示:
(1)、 , , 三种套餐每月所需费用 (元)与每月通话时间 (分)之间的函数关系如图所示:①直接写出 , 的值.
②上月快递员甲、乙分别使用套餐 、 ,已知甲、乙通话时间相同,但甲、乙实际费用相差18元,求上月甲通话时间多少分钟?
(2)、若快递员月配送量在3080单至3220单之间(包括3080单和3220单),每单采用打电话或发短信告知,且每单告知1次,公司规定发短信单数不超过总单数的 .了解到:套餐 赠送400条短信,套餐 , 均可用10元购买600条短信包(限购1次),国内短信超出部分按0.1元/条计费.请通过计算选择一种套餐,使总费用较少.(注:打电话1分钟/单,发短信1条/单.)24. 如图,在矩形 中, 于点 ,交 边于点 . 平分 交 于点 ,并经过 边的中点 . (1)、求证: .(2)、求 的值.(3)、若 ,试在 上找一点 (不与 , 重合),使直线 经过四边形 一边的中点,求所有满足条件的 的值.
(1)、求证: .(2)、求 的值.(3)、若 ,试在 上找一点 (不与 , 重合),使直线 经过四边形 一边的中点,求所有满足条件的 的值.