浙江省温州市泰顺县2022年九年级中考模拟考试数学试卷

试卷更新日期：2022-06-02 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分．每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1. 计算（-3）²的结果是（）

A、9 B、-9 C、6 D、-6

查看试题解析
2. 冬奥会的吉祥物冰墩墩在抖音上的视频播放量超26 100 000 000次，关注人数超5亿，面临“一墩难求”的窘境，其中数据26 100 000 000用科学记数法表示为（）

A、261×10¹¹ B、2.61×10¹⁰ C、0.261×10¹³ D、26.1×10⁹

查看试题解析
3. 如图所示的几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 2022 年冬奥会吉祥物为“冰墩墩"，冬残奥会吉祥物为“雪容融”．现有6张不透明卡片，卡片除正面图案不同外，其余均相同，其中2张正面印有“冰墩墩"，4张正面印有“雪容融”。将6张卡片正面向下洗匀，从中随机抽取一张卡片为“冰墩墩”的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析
5. 乐器古筝示意图如图所示，弦AB的黄金分割点C是称为玛子的支撑物，若AB=8分米，则玛子离较远的端点A的距离为（）

A、（4 $\sqrt{5}$ +4）分米 B、（4 $\sqrt{5}$ -4）分米 C、（12-4 $\sqrt{5}$ ）分米 D、（8-4 $\sqrt{5}$ ）分米

查看试题解析
6. 如图，在 $▱$ ABCD中，AB=8，AD=6，∠BAD的平分线交CD于点E，则CE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 我国明代数学读本《算法统宗》一书中有这样一道题：“一支竿一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托。”其大意为：现有一根竿和一条绳索，如果用绳索去量竿，绳索比竿长5尺：如果将绳索对折后再去量竿，就比竿短5尺。设索长x尺，竿长y尺，则可列方程组为（）

A、 ${\begin{cases} x + y = 5 \\ 2 x - y = 5 \end{cases}$ B、 ${\begin{cases} y - x = 5 \\ 2 x - y = 5 \end{cases}$ C、 ${\begin{cases} x - y = 5 \\ y - \frac{x}{2} = 5 \end{cases}$ D、 ${\begin{cases} x - y = 5 \\ \frac{x}{2} - y = 5 \end{cases}$

查看试题解析
8. 如图，在点O处的船只准备沿垂直河岸l₁的路线OA驶向对岸12，但受水流的影响，实际路线比计划路线偏离a度，测得河宽为20米，则实际比原计划多行驶了（）．

A、（ $\frac{20}{\sin α}$ -20）米 B、（ $\frac{20}{\cos α}$ -20）米 C、（20sinα-20）米 D、（20cosα-20）米

查看试题解析
9. 已知直线l交抛物线y=x²-2x-8于点A（-4，m），B（5，7）．若点P在抛物线上且在直线l的下方（不与点A，B重合），则点P纵坐标y的取值范围是（）

A、7<y<16 B、7≤y≤16 C、-9<y<16 D、-9≤y<16

查看试题解析
10. 中国古代数学家张爽证明勾股定理的弦图如图所示，它由四个全等的直角三角形和．一个小正方形EFGH组成，恰好拼成大正方形ABCD．作直线EG分别交AD，BC于点M， N．若图中两个正方形的面积分别是13和1，则MN的长为（）

A、 $3 \sqrt{2}$ B、 $\frac{14 \sqrt{2}}{5}$ C、 $\frac{13 \sqrt{2}}{5}$ D、 $\frac{12 \sqrt{2}}{5}$

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分）

11. 分解因式：m²-6m+9= .

查看试题解析
12. 不等式组 ${\begin{cases} 3 + x \geq - 2 \\ \frac{4 - x}{2} > 1 \end{cases}$ 的解为

查看试题解析
13. 若扇形的圆心角为120°，半径为9，则面积为

查看试题解析
14. 泰顺2022年4月1日至7日的气温折线图如图所示，这一周中温差最大的是4月日．

查看试题解析
15. 如图，等腰△ABC的顶角∠ABC=120°，AB=BC，腰AB垂直y轴，垂足为A，AB的中点D和点C恰好落在反比例函数y= $\frac{k}{x}$ （k>0）上．若AC=2 $\sqrt{3}$ ，则k的值是．

查看试题解析
16. 如图1是将正方形分割成七个几何图形得到的七巧板，它是中国古代劳动人民发明的一种智力玩具．图2是由七巧板拼成“熊”的几何图形．四边形ABCD是菱形，且CIJ的面积为2，则AE= ．记点K到直线LG的距离为d，则 $\frac{d}{A B}$ =

查看试题解析

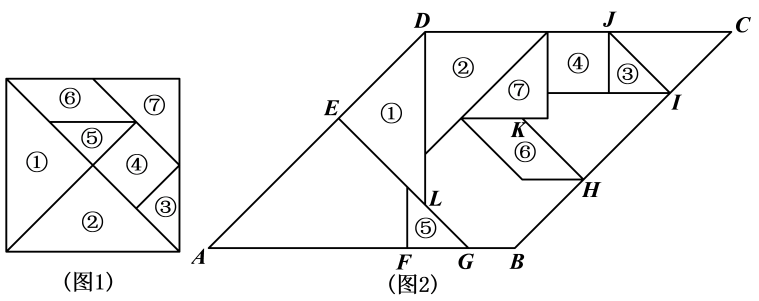
三、解答题（本题有8小题，共80分解答需写出必要的文字说明、演算步骤或证明过程）

17.

(1)、计算：-2×3+ $\sqrt{8}$ -2022⁰+|4|

(2)、化简： $\frac{x^{2}}{x + 1} - \frac{1}{x + 1}$

查看试题解析
18. 已知，如图，点B，E，D，C在同一直线上，AB=AC，AD=AE．

(1)、求证：BE=CD．
针对这道题，三位同学进行如下讨论；

兰兰：“由AB=AC得∠B=∠C，又因为AE=AD，

通过证明△ABE≌△ACD，可得"

花花；“兰兰的全等条件是‘边边角'。不能证明全等，

但我用‘角角边'可证△ABE≌ACD．"

草草：“还可证明△ABD≌△ACE得BD=CE．再得BE=CD：但图中有两个等腰三角形，我认为最简洁的方法是用'三线合一'的性质证明．"

请你结合上述讨论，选择恰当的方法完成证明．

(2)、若∠BAC=90°，ED=4，BE=2，求AB的长．

查看试题解析

19. 基于对“校园落叶变废为宝"的研究，某科学兴趣小组在校内的“猕猴桃种植基地”进行落叶堆肥实验。控制猕猴桃其它生长条件不变，其中一半的猕猴桃植株施落叶肥料（甲组），另一半植株只用无机肥（乙组）．进入猕猴桃的收获期时，为研究落叶堆肥实验的效果，从两组中各随机摘取50个猕猴桃，测量单果质量x（g）．现将测量结果分成5组，A：40≤x<60，B：60≤x <80，C：80≤x<100， D：100≤x<120， E：120x<140，并绘制成如下统计图．其中100g及以上的果子，称为优质大果，更受市场欢迎．

(1)、填写以下表格．

	平均数	中位数	大果率	方差
甲组	（）	落（）组	（）	7.04
乙组	79.6	落B组	20%	23.64

(2)、结合平均数、中位数、大果串、方差进行分析，多角度评价“落叶堆肥"的实际效果．

查看试题解析

20. 如图，在所给的方格纸中，每个小正方形边长都是1，点A，B位于格点处．

(1)、在图1中画出格点△ABC，使AC²+BC²=6．

(2)、在图2中画出格点四边形AEBF，使四边形AEBF的对角线互相垂直平分．

查看试题解析
21. 已知抛物线y=-x²+bx+c经过点（0，2）与（2，0）．

(1)、求该抛物线的函数关系式．

(2)、此抛物线向下平移m个单位后，顶点落在直线y=2r上，求平移后抛物线与y轴的交点坐标．

查看试题解析
22. 如图，锐角△ABC内接于⊙O，AB=AC，BD为直径，过点B作BF⊥AB交⊙O于点E，交DC的延长线于点F．

(1)、求证：∠ABD=∠CBF．

(2)、连结DE，若DE=20，sin∠A= $\frac{24}{25}$ ，求BF的长．

查看试题解析
23. 猕猴桃被誉为“维C之王”，其中含血清促进素可以稳定情绪，丰富膳食纤维能促进心脏健康．在泰顺猕猴桃销售旺季时，爸爸妈妈让他们的两个孩子泰泰与顺顺去猕猴桃市场采购相同价格的同一种猕猴桃．泰泰用240元买的猕猴桃数量比顺顺用300元买的猕猴桃数量少10斤．

(1)、求这种猕猴桃的单价．

(2)、两人第二次再去采购该种猕猴桃时，每斤单价比上次少了2元．两个人购买方案不同如图所示．他们想通过这两次购买体验，作为数学项目化学习的一个素材，探究谁的购买方案更加合算．计算得泰泰两次购买的猕猴桃平均价格是元/斤，顺顺两次购买的猕猴桃平均价格是元/斤．

(3)、泰泰和顺顺通过这次购买弥猴桃的项目化学习，总结出连续购买某种商品更合算的方案，并迁移联想到爸爸的加油习惯是按照同样的金额加油，而妈妈总是说"把油箱加满"。他们要建议父母按相同的（填“金额”或“油量"）加油更合算．请你通过计算说明理由．

查看试题解析
24. 在矩形ABCD中，BC=2AB，点E是对角线AC上任意一点，过点E作AD的垂线分别交AD，BC于点F，G，作FH平行AC交CD于点H．

(1)、证明：EF=CH．

(2)、连结GH交AC于点K，若AE：CK=3，求AE：EK的值．

(3)、作△FGH的外接圆⊙O，且AB=1．
①若⊙O与矩形的边相切时，求CH的长．

②作点E关于GH的对称点E'，当E'落在⊙O上时，直接写出△FGH的面积。

查看试题解析