广西河池市2022年初中学业水平模拟考试数学试卷
试卷更新日期:2022-06-02 类型:中考模拟
一、单选题
-
1. 计算的结果是( )A、3 B、1 C、-1 D、-32. 如图, , 是截线, , 则的度数是( )
 A、 B、 C、 D、3. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
A、 B、 C、 D、3. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 关于x的一元一次不等式3x≤4+x的解集在数轴上表示为( )A、
4. 下列计算正确的是( )A、 B、 C、 D、5. 关于x的一元一次不等式3x≤4+x的解集在数轴上表示为( )A、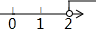 B、
B、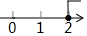 C、
C、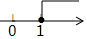 D、
D、 6. 小明连续5天的体温数据如下(单位:℃):36.6,36.2,36.5,36.2,36.3.关于这组数据,下列说法正确的是( )A、中位数是36.5 B、众数是36.2 C、平均数是36.3 D、方差是36.67. 如图,在中, , , , 垂足为 , 则的长是( )
6. 小明连续5天的体温数据如下(单位:℃):36.6,36.2,36.5,36.2,36.3.关于这组数据,下列说法正确的是( )A、中位数是36.5 B、众数是36.2 C、平均数是36.3 D、方差是36.67. 如图,在中, , , , 垂足为 , 则的长是( )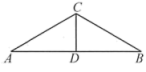 A、 B、 C、2 D、38. 陈师傅应客户要求加工4个长为4cm、宽为3cm的矩形零件.在交付客户之前,陈师傅需要对4个零件进行检测.根据零件的检测结果,图中有可能不合格的零件是( )A、
A、 B、 C、2 D、38. 陈师傅应客户要求加工4个长为4cm、宽为3cm的矩形零件.在交付客户之前,陈师傅需要对4个零件进行检测.根据零件的检测结果,图中有可能不合格的零件是( )A、 B、
B、 C、
C、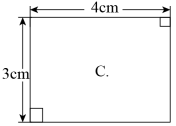 D、
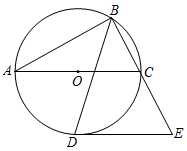
D、 9. 已知反比例函数 ,当 ,则下列结论正确的是( )A、 B、 C、 D、10. 若关于x的方程x2-4x+m=0有两个相等的实数根,则m的值是( )A、1 B、2 C、4 D、±411. 《孙子算经》是中国古代最重要的数学著作.其中记载:“今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺.木长几何?”译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木多少尺?”设绳子长尺,木长尺,可列方程组是( )A、 B、 C、 D、12. 如图,的内切圆⊙与 , , 分别相切于点 , , , , , , 则的长是( )
9. 已知反比例函数 ,当 ,则下列结论正确的是( )A、 B、 C、 D、10. 若关于x的方程x2-4x+m=0有两个相等的实数根,则m的值是( )A、1 B、2 C、4 D、±411. 《孙子算经》是中国古代最重要的数学著作.其中记载:“今有木,不知长短,引绳度之,余绳四尺五寸,屈绳量之,不足一尺.木长几何?”译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木多少尺?”设绳子长尺,木长尺,可列方程组是( )A、 B、 C、 D、12. 如图,的内切圆⊙与 , , 分别相切于点 , , , , , , 则的长是( ) A、3.5 B、4 C、4.5 D、5
A、3.5 B、4 C、4.5 D、5二、填空题
-
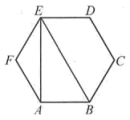
13. 若分式 有意义,则 的取值范围是.14. 因式分解:x2-25=.15. 如图,在正六边形中,则的值为.
 16. 已知 , , 三点在二次函数的图象上,则 , , 的大小关系是(用“<”号表示).
16. 已知 , , 三点在二次函数的图象上,则 , , 的大小关系是(用“<”号表示).三、解答题
-
17. 计算:.18. 先化简,再求值: , 其中 , .19. 如图,在中,.
 (1)、尺规作图:在上截取 , 使得(不写作法,保留作图痕迹,用黑色笔将痕迹加黑);(2)、在(1)所作的图形中,连接 , 证明:.20. 一次课外实践活动中,某班数学小组测量旗杆的高度如图,测角仪高度米,在处用测角仪测得旗杆顶端的仰角 , 沿旗杆方向直走20米到达处,再次测得旗杆顶端的仰角.求旗杆的高度.
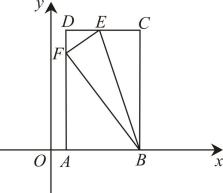
(1)、尺规作图:在上截取 , 使得(不写作法,保留作图痕迹,用黑色笔将痕迹加黑);(2)、在(1)所作的图形中,连接 , 证明:.20. 一次课外实践活动中,某班数学小组测量旗杆的高度如图,测角仪高度米,在处用测角仪测得旗杆顶端的仰角 , 沿旗杆方向直走20米到达处,再次测得旗杆顶端的仰角.求旗杆的高度.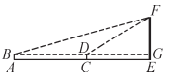 21. 如图,在平面直角坐标系中,的顶点 , 在坐标轴上, , , , 求所在直线的解析式.
21. 如图,在平面直角坐标系中,的顶点 , 在坐标轴上, , , , 求所在直线的解析式. 22. 2021年12月9日“天宫课堂”第一课开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课,神奇的太空实验堪称宇宙级精彩!某校为了培养学生对航天知识的学习兴趣,组织了800名学生进行了“航天知识竞赛”,该校从中随机抽取了名学生的竞赛成绩分成四组(满分100分,每名学生的成绩记为分),得到如下未完整的频数分布表、频数分布直方图和扇形统计图.根据图中信息,解答下列问题:
22. 2021年12月9日“天宫课堂”第一课开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课,神奇的太空实验堪称宇宙级精彩!某校为了培养学生对航天知识的学习兴趣,组织了800名学生进行了“航天知识竞赛”,该校从中随机抽取了名学生的竞赛成绩分成四组(满分100分,每名学生的成绩记为分),得到如下未完整的频数分布表、频数分布直方图和扇形统计图.根据图中信息,解答下列问题:分组
频数
:
:
18
:
24
:
 (1)、求 , , 的值;(2)、请补全频数分布直方图;(3)、若规定竞赛成绩为优秀,请估算全校竞赛成绩达到优秀的学生人数;(4)、竞赛结束后,九年级一班从本班获得优秀()的甲、乙、丙、丁四名同学中随机抽取两名宣讲航天知识.请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.23. 某汽车贸易公司销售A、B两种型号的新能源汽车,A型车进货价格为每台12万元,B型车进货价格为每台15万元,该公司销售2台A型车和5台B型车,可获利3.1万元,销售1台A型车和2台B型车,可获利1.3万元.(1)、求销售一台A型、一台B型新能源汽车的利润各是多少万元?(2)、该公司准备用不超过300万元资金,采购A、B两种新能源汽车共22台,问最少需要采购A型新能源汽车多少台?
(1)、求 , , 的值;(2)、请补全频数分布直方图;(3)、若规定竞赛成绩为优秀,请估算全校竞赛成绩达到优秀的学生人数;(4)、竞赛结束后,九年级一班从本班获得优秀()的甲、乙、丙、丁四名同学中随机抽取两名宣讲航天知识.请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.23. 某汽车贸易公司销售A、B两种型号的新能源汽车,A型车进货价格为每台12万元,B型车进货价格为每台15万元,该公司销售2台A型车和5台B型车,可获利3.1万元,销售1台A型车和2台B型车,可获利1.3万元.(1)、求销售一台A型、一台B型新能源汽车的利润各是多少万元?(2)、该公司准备用不超过300万元资金,采购A、B两种新能源汽车共22台,问最少需要采购A型新能源汽车多少台?