广西贵港市港北区2022年初中学业水平模拟考试数学试题(二)
试卷更新日期:2022-06-02 类型:中考模拟
一、单选题
-
1. 2的绝对值是( )A、-2 B、2 C、0 D、32. 如图所示的几何体的主视图是( )
 A、
A、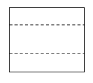 B、
B、 C、
C、 D、
D、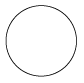 3. 将数化为小数是( )A、0.000025 B、0.0000025 C、0.00025 D、0.000000254. 在今年的5月的体育中考中,某校7名学生的分数分别是:60,57,58,59,58,56,58,则下列表述错误的是( )A、中位数是59 B、平均数是58 C、众数是58 D、极差是45. 下列运算正确的是( )A、 B、 C、 D、6. 已知点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,则点P的坐标为( )A、(4,﹣2) B、(﹣4,2) C、(﹣4,4) D、(2,﹣4)7. 不等式组的整数解是一个一元二次方程的两根,则该方程为( )A、 B、 C、 D、8. 下列命题中是真命题的是( )A、绝对值等于它本身的数是0和1 B、等弦所对的圆周角相等 C、对角线互相垂直的平行四边形是菱形 D、两条直线被第三条直线所截,内错角相等9. 从1、2、3三个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程没有实数根的概率为( )A、 B、 C、 D、10. 如图,与是的两条互相垂直的弦,交点为点 , , 点在圆上,则的度数为( )
3. 将数化为小数是( )A、0.000025 B、0.0000025 C、0.00025 D、0.000000254. 在今年的5月的体育中考中,某校7名学生的分数分别是:60,57,58,59,58,56,58,则下列表述错误的是( )A、中位数是59 B、平均数是58 C、众数是58 D、极差是45. 下列运算正确的是( )A、 B、 C、 D、6. 已知点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,则点P的坐标为( )A、(4,﹣2) B、(﹣4,2) C、(﹣4,4) D、(2,﹣4)7. 不等式组的整数解是一个一元二次方程的两根,则该方程为( )A、 B、 C、 D、8. 下列命题中是真命题的是( )A、绝对值等于它本身的数是0和1 B、等弦所对的圆周角相等 C、对角线互相垂直的平行四边形是菱形 D、两条直线被第三条直线所截,内错角相等9. 从1、2、3三个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程没有实数根的概率为( )A、 B、 C、 D、10. 如图,与是的两条互相垂直的弦,交点为点 , , 点在圆上,则的度数为( )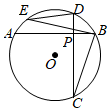 A、 B、 C、 D、11. 如图,矩形纸片ABCD中,AD=9,E是CD上一点,连结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为G.若AG=6,则DE的值为( )
A、 B、 C、 D、11. 如图,矩形纸片ABCD中,AD=9,E是CD上一点,连结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为G.若AG=6,则DE的值为( )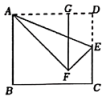 A、 B、 C、 D、512. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连接EN、EF.有以下结论:①②AN=EN③BE+DF=EF④当AE=AF时, , 则正确的结论有( )
A、 B、 C、 D、512. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连接EN、EF.有以下结论:①②AN=EN③BE+DF=EF④当AE=AF时, , 则正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
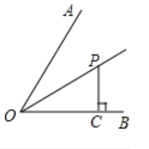
13. 计算:.14. 因式分解: .15. 如图,OP为∠AOB的平分线,PC⊥OB于点C,且 , , 点P的OA距离为.
 16. 如图,在平面直角坐标系中,点A,B在反比例函数图像(第一象限)上运动,且始终保持线段的长度不变.M为线段AB的中点,连接OM.则线段OM长度的最小值是.
16. 如图,在平面直角坐标系中,点A,B在反比例函数图像(第一象限)上运动,且始终保持线段的长度不变.M为线段AB的中点,连接OM.则线段OM长度的最小值是. 17. 如图,正方形ABCD的边长为 , M为对角线BD的四等分点(BM<DM),连接AM,将△ABM绕点B顺时针旋转45°得到 , 则AM边扫过的阴影部分的面积为.
17. 如图,正方形ABCD的边长为 , M为对角线BD的四等分点(BM<DM),连接AM,将△ABM绕点B顺时针旋转45°得到 , 则AM边扫过的阴影部分的面积为. 18. 定义运算“※”: , 如:.若函数的图象过点 , 将该函数图象向右平移,当它再次经过点P时,所得的图象函数表达式为.
18. 定义运算“※”: , 如:.若函数的图象过点 , 将该函数图象向右平移,当它再次经过点P时,所得的图象函数表达式为.三、解答题
-
19. 计算(1)、计算:.(2)、解分式方程:.20. 如图,△ABC中,AB=AC,∠ABC=75°,
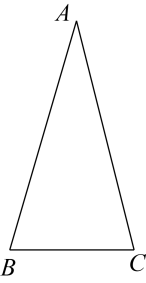 (1)、请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AC于F;(不要求写作法,保留作图痕迹)(2)、在(1)条件下,连接BF,则∠CBF=.21. 如图,已知反比例函数的图象经过点 , 过A作AC⊥y轴于点C.点B为反比例函数图象上的一动点,过点B作BD⊥x轴于点D,直线BC与x轴的负半轴交于点E.
(1)、请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AC于F;(不要求写作法,保留作图痕迹)(2)、在(1)条件下,连接BF,则∠CBF=.21. 如图,已知反比例函数的图象经过点 , 过A作AC⊥y轴于点C.点B为反比例函数图象上的一动点,过点B作BD⊥x轴于点D,直线BC与x轴的负半轴交于点E. (1)、求反比例函数的表达式;(2)、若BD=3OC,求△BDE的面积.22. 为了响应市政府号召,某中学开展了“六城同创与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)、求反比例函数的表达式;(2)、若BD=3OC,求△BDE的面积.22. 为了响应市政府号召,某中学开展了“六城同创与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图. (1)、本次随机调查的学生人数是人;(2)、请你补全条形统计图;(3)、在扇形统计图中,“B”所在扇形的圆心角等于度;(4)、该市有中学生3万人,请你估算该市中学生参加“C:交通安全”活动的人数有多少?23. 为提高教学质量,市教育局准备采购若干套投影设备升级各学校教学硬件,经考察,公司有 、 两种型号的投影设备可供选择.(1)、该公司2020年年初每套 型投影设备的售价为 万元,经过连续两次降价,年底套售价为 万元,求每套 型投影设备平均下降率 ;(2)、2020年年底市教育局经过招标,决定采购并安装该公司 , 两种型号的投影设备共 套,采购专项经费总计不超过 万元,采购合同规定:每套 型投影设备价为 万元,每套 型投影设备售价为 万元,则 型投影设备最多可购多少套?24. 如图,AB是圆O的直径,点D在直径AB上(D与A,B不重合),CD⊥AB,且CD=AB,连接CB与圆O交于点F,在CD上取一点E,使得EF=EC.
(1)、本次随机调查的学生人数是人;(2)、请你补全条形统计图;(3)、在扇形统计图中,“B”所在扇形的圆心角等于度;(4)、该市有中学生3万人,请你估算该市中学生参加“C:交通安全”活动的人数有多少?23. 为提高教学质量,市教育局准备采购若干套投影设备升级各学校教学硬件,经考察,公司有 、 两种型号的投影设备可供选择.(1)、该公司2020年年初每套 型投影设备的售价为 万元,经过连续两次降价,年底套售价为 万元,求每套 型投影设备平均下降率 ;(2)、2020年年底市教育局经过招标,决定采购并安装该公司 , 两种型号的投影设备共 套,采购专项经费总计不超过 万元,采购合同规定:每套 型投影设备价为 万元,每套 型投影设备售价为 万元,则 型投影设备最多可购多少套?24. 如图,AB是圆O的直径,点D在直径AB上(D与A,B不重合),CD⊥AB,且CD=AB,连接CB与圆O交于点F,在CD上取一点E,使得EF=EC. (1)、求证:EF是圆O的切线;(2)、若D是OA的中点,AB=4,求CF的长.25. 如图,已知抛物线经过ABC的三个顶点,其中点A(0,1),点B(-9,10),轴,点P是直线AC下方抛物线上的动点.
(1)、求证:EF是圆O的切线;(2)、若D是OA的中点,AB=4,求CF的长.25. 如图,已知抛物线经过ABC的三个顶点,其中点A(0,1),点B(-9,10),轴,点P是直线AC下方抛物线上的动点.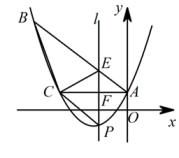 (1)、直接写出:b= , c=;(2)、过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与ABC相似,若存在,直接写出点Q的坐标,若不存在,请说明理由.26. 有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,∠ADB=30°.
(1)、直接写出:b= , c=;(2)、过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与ABC相似,若存在,直接写出点Q的坐标,若不存在,请说明理由.26. 有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,∠ADB=30°.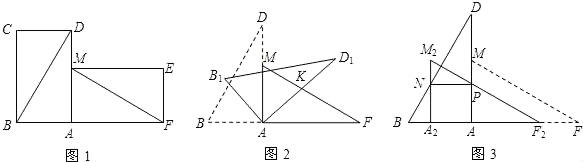 (1)、试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;(2)、把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1 , 边AD1交FM 于点K(如图2),设旋转角为β(0°<β<90°),当△AFK 为等腰三角形时,求β的度数;(3)、若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.
(1)、试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;(2)、把△BCD 与△MEF 剪去,将△ABD绕点A顺时针旋转得△AB1D1 , 边AD1交FM 于点K(如图2),设旋转角为β(0°<β<90°),当△AFK 为等腰三角形时,求β的度数;(3)、若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离.