浙江省金华市义乌市2022届高三下学期数学5月适应性考试试卷

试卷更新日期：2022-06-02 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = R$ ，集合 $P = {x | - 2 < x < 1}$ ， $Q = {x | x \geq 0}$ ，则 $P ∩ (∁_{U} Q) =$ （）

A、 $(- 2 ， 0)$ B、 $(0 ， 1)$ C、 $(- \infty ， 0) ∪ (0 ， 1)$ D、 $(- \infty ， 1)$

查看试题解析
2. 已知实数a，b， $a > 0$ ， $b > 0$ ，则“ $a + b < 2$ ”是“ $\sqrt{a} < \sqrt{2 - b}$ ”（）

A、必要不充分条件 B、充分不必要条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
3. 已知 $m, n$ 是两条不同直线， $α, β, γ$ 是三个不同平面，下列命题中正确的是（）

A、若 $m ‖ α, n ‖ α,$ 则 $m ‖ n$ B、若 $α ⊥ γ, β ⊥ γ,$ 则 $α ‖ β$ C、若 $m ‖ α, m ‖ β,$ 则 $α ‖ β$ D、若 $m ⊥ α, n ⊥ α,$ 则 $m ‖ n$

查看试题解析
4. 若实数x，y满足约束条件 ${\begin{array}{l} x + y - 1 \geq 0 \\ y \geq | 2 x - 1 | \end{array}$ ，则 $z = x + 2 y$ 的取值范围是（）

A、 $[\frac{1}{2} ， \frac{4}{3}]$ B、 $[\frac{1}{2} ， 2]$ C、 $[\frac{4}{3} ， + \infty)$ D、 $[2 ， + \infty)$

查看试题解析
5. 先将函数 $f (x) = s i n (x - \frac{π}{3})$ 图象上各点的横坐标缩短为原来的 $\frac{1}{2}$ ，再把所得函数图象向左平移 $\frac{π}{6}$ 个单位长度，得到函数 $g (x)$ 的图象，则下列说法错误的是 $（）$

A、函数 $g (x)$ 是奇函数 B、函数 $g (x)$ 的最小正周期是 $π$ C、函数 $g (x)$ 图像关于直线 $x = \frac{π}{4} + k π (k \in Z)$ 对称 D、函数 $g (x)$ 在 $(- \frac{π}{6} ， \frac{π}{3})$ 上单调递增

查看试题解析
6. 若函数 $f (x) = a^{x} + a c o s x (a > 0)$ ，则下列图象不可能是（）

A、 B、 C、 D、

查看试题解析
7. 若函数 $f (x) = x (2^{x} - 2^{- x})$ ，设 $a = \frac{1}{2}$ ， $b = l o g_{4} \frac{1}{3}$ ， $c = l o g_{5} \frac{1}{4}$ ，则下列选项正确的是（）

A、 $f (a) < f (b) < f (c)$ B、 $f (a) < f (c) < f (b)$ C、 $f (b) < f (a) < f (c)$ D、 $f (c) < f (a) < f (b)$

查看试题解析
8. 已知集合 $A = {4 ， 5 ， 6 ， 7}$ ， $B = {5 ， 6 ， 7 ， 8 ， 9}$ ，从集合A中取出1个元素，从集合B中取出3个元素，可以组成无重复数字且比5000大的自然数共有（）

A、180 B、300 C、468 D、564

查看试题解析
9. 已知双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ ， $O$ 为坐标原点， $F$ 为双曲线 $C$ 的左焦点，若 $C$ 的右支上存在一点 $P$ ，使得 $△ O F P$ 外接圆 $M$ 的半径为 $1$ ，且四边形 $M F O P$ 为菱形，则双曲线 $C$ 的离心率是（）

A、 $\sqrt{2} + 1$ B、 $\sqrt{3} + 1$ C、 $\sqrt{3} - 1$ D、2

查看试题解析
10. 已知数列 ${a_{n}}$ ， ${b_{n}}$ 满足 $a_{1} = 2$ ， $b_{1} = \frac{1}{2}$ ， ${\begin{array}{l} a_{n + 1} = b_{n} + \frac{1}{a_{n}} \\ b_{n + 1} = a_{n} + \frac{1}{b_{n}} \end{array} ， n \in N^{*}$ ，则下列选项错误的是（）

A、 $\frac{a_{2}}{b_{2}} = \frac{1}{4}$ B、 $a_{50} \cdot b_{50} < 112$ C、 $a_{50} + b_{50} = \frac{5}{2} \sqrt{a_{50} \cdot b_{50}}$ D、 $| a_{50} - b_{50} | \leq 15$

查看试题解析

二、填空题

11. 已知i是虚数单位，复数 $i z = 1 + i$ ，则 $z =$ ．

查看试题解析
12. 某几何体的三视图（单位：cm）如图所示，其中正视图是等边三角形，则此几何体的体积是．

查看试题解析
13. 已知平面向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 满足 $\vec{c} \cdot \vec{a} = \vec{c} \cdot \vec{b} = | \vec{a} | = | \vec{b} | = 1$ ，当 $(\vec{a} - \vec{c}) \cdot (\vec{b} - \vec{c})$ 取到最小值吋，对任意实数 $λ$ ， $| λ \vec{a} + (1 - λ) \vec{b} |$ 的最小值是．

查看试题解析
14. 已知直线 $l_{1}$ ： $a x + y + 1 = 0$ ， $l_{2}$ ： $x + a y + 1 = 0$ ．若 $l_{1} ∥ l_{2}$ ，则 $a =$ ，此时 $l_{1}$ 与 $l_{2}$ 之间的距离为．

查看试题解析
15. 已知 $(x + 1) {(x - 2)}^{4} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5}$ ，则 $a_{1} =$ ， $a_{2} + a_{3} + a_{4} + a_{5}$ $=$ ．

查看试题解析
16. 某高中数学社团招募成员，依次进行笔试，面试两轮选拔，每轮结果都分“合格”和“不合格”.当参选同学在第一轮笔试中获得“合格”时，才能进入下一轮面试选拔，两轮选拔都合格的同学入选到数学社团.现有甲同学参加数学社团选拔，已知甲同学在笔试，面试选拔中获得“合格”和“不合格”的概率分别为 $\frac{2}{3}$ ， $\frac{p}{3}$ ，且在笔试，面试两轮选拔中取得的成绩均相互独立，互不影响且概率相同，则甲同学能进入到数学社团的概率是，设甲同学在本次数学社团选拔中恰好通过X轮选拔，则数学期望 $E (X) =$ ．

查看试题解析
17. 设 $a \in R$ ．函数 $f (x) = {\begin{array}{l} 2 e^{x} - 1 ， & x \leq 0 \\ a x^{2} + (a^{2} - 2) x - l n x ， & x > 0 \end{array}$ ，若 $f (f (0)) = 0$ ，则 $a =$ ，若 $f (x)$ 只有一个零点，则a $的$ 取值范围是．

查看试题解析

三、解答题

18. 如图， $△ A B C$ 中， $A C ⊥ B C$ ， $A = \frac{π}{3}$ ， $| A C | = 2$ ，点D是以BC为直径的半圆弧上的动点，满足 $∠ C B D = α$ ， $\frac{π}{4} \leq α < \frac{π}{2}$ ．过点D作 $D E ∥ A B$ 交AC于点E，作 $D F ∥ A C$ 交AB于点F．

(1)、试用α表示BD的长度；

(2)、求 $| D E | + | D F |$ 的取值范围．

查看试题解析
19. 如图，在四棱锥P-ABMN中，△PNM是边长为2的正三角形，AN⊥NP， $A N ∥ B M$ ， $A N = 3$ ， $B M = 1$ ， $A B = 2 \sqrt{2}$ ， C，D分別是线段AB，PN的中点．

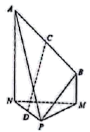(1)、求证： $C D ∥$ 平面PBM；

(2)、求直线CD与平面ABP所成用的正弦值．

查看试题解析
20. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $a_{1} = 1$ ，又 $a_{n}$ ， $\sqrt{2 S_{n}}$ ， $a_{n + 1} (n \in N^{*})$ 成等比数列．

(1)、求数列 ${a_{n}}$ 的通项公式：

(2)、求 $S_{2 n}$ ，并证明 $\frac{1}{S_{4}} + \frac{1}{S_{6}} + \frac{1}{S_{8}} + ⋯ + \frac{1}{S_{2 n + 2}} > \frac{n}{4 (n + 2)}$ ．

查看试题解析
21. 如图，已知点P在直线l： $x = - 2$ 上，A，B为抛物线C： $y^{2} = 2 p x (p > 0)$ 上任意两点，PA，PB均与抛物线C相切，直线AB与直线l交于点Q，过抛物线C的焦点F作AB的垂线交直线l于点K．

(1)、若点A到F的距离比到直线l的距离小1，求抛物线C的方程；

(2)、在（1）的条件下，当 $| K Q |$ 最小时，求 $\frac{| A B |}{| K Q |}$ 的值．

查看试题解析
22. 设函数 $f (x) = \frac{1}{2} x^{2} + a x - (a x + 1) l n x (a \in R)$ ，记 $f (x)$ 的导数为 $g (x)$ ．

(1)、讨论 $g (x)$ 的单调性；

(2)、若 $f (x)$ 有三个不同的极值点 $x_{1}$ ， $x_{2}$ ， $x_{3} (x_{1} < x_{2} < x_{3})$ ，证明： $f (x_{3}) < f (x_{1}) < f (x_{2})$ ．

查看试题解析