浙江省嘉兴市海宁市2022届高三下学期数学5月适应性考试试卷
试卷更新日期:2022-06-02 类型:高考模拟
一、单选题
-
1. 设全集 , 集合 , 则( )A、 B、 C、 D、2. 已知复数z满足(i为虚数单位),则z的虚部为( )A、2 B、-2 C、1 D、-13. 设 , 则“”是“”的( ).A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 已知双曲线C的渐近线方程为 , 且焦距为10,则双曲线C的标准方程是( )A、 B、 C、或 D、或5. 某几何体的三视图如图所示(单位:),则该几何体的体积(单位:)是( )
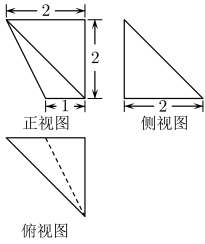 A、9 B、6 C、3 D、26. 已知实数满足约束条件 , 则的最大值是( )A、10 B、7 C、5 D、27. 如图为函数的部分图象,则的值可能是( )
A、9 B、6 C、3 D、26. 已知实数满足约束条件 , 则的最大值是( )A、10 B、7 C、5 D、27. 如图为函数的部分图象,则的值可能是( )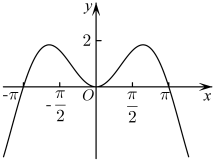 A、4 B、3 C、2 D、18. 如图,在矩形中, , E,F,G,H分别为边的中点,将分别沿直线翻折形成四棱锥 , 下列说法正确的是( )
A、4 B、3 C、2 D、18. 如图,在矩形中, , E,F,G,H分别为边的中点,将分别沿直线翻折形成四棱锥 , 下列说法正确的是( ) A、异面直线所成角的取值范围是 B、异面直线所成角的取值范围是 C、异面直线所成角的取值范围是 D、异面直线所成角的取值范围是9. 2022年第二十四届北京冬奥会开幕式上由96片小雪花组成的大雪花惊艳了全世界,数学中也有一朵美丽的雪花一“科赫雪花”.它可以这样画,任意画一个正三角形 , 并把每一边三等分:取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉,形成雪花曲线;重复上述两步,画出更小的三角形.一直重复,直到无穷,形成雪花曲线, .
A、异面直线所成角的取值范围是 B、异面直线所成角的取值范围是 C、异面直线所成角的取值范围是 D、异面直线所成角的取值范围是9. 2022年第二十四届北京冬奥会开幕式上由96片小雪花组成的大雪花惊艳了全世界,数学中也有一朵美丽的雪花一“科赫雪花”.它可以这样画,任意画一个正三角形 , 并把每一边三等分:取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉,形成雪花曲线;重复上述两步,画出更小的三角形.一直重复,直到无穷,形成雪花曲线, .
设雪花曲线的边长为 , 边数为 , 周长为 , 面积为 , 若 , 则下列说法正确的是( )
A、 B、 C、均构成等比数列 D、10. 平面直角坐标系中,若两点 , 满足或 , 则称点S和点T保持了合理间距.正方形中,顶点 , 动点P,Q都在正方形内(包括边界),且点P在抛物线上,则下列说法错误的是( )A、若点P与点O,A,B都保持了合理间距,则点P的横坐标的取值范围是 B、若点Q与点O,A,B都保持了合理间距,则点Q的轨迹所形成的面积为6 C、若点Q与点P,O,A,B都保持了合理间距,则点Q的轨迹所形成的面积最大值为6 D、若点Q与点P,O,A,B都保持了合理间距,则点Q的轨迹所形成的面积最小值为二、填空题
-
11. 直线的倾斜角为 , 若位于第一象限的动点在直线上,则的最大值为 .12. 已知多项式 , 则 , .13. 在一次投篮训练中,甲同学每次投篮投中的概率为 , 乙和丙同学每次投篮投中的概率均为 , 每人各投1次,记为三人投中的总次数,则; .14. 在中,已知 , 则 , .15. 已知函数 , 若方程有4个不同的实数解,则实数a的取值范围为 .16. 如图,点F为椭圆的左焦点,直线分别与椭圆C交于A,B两点,且满足 , O为坐标原点,若 , 则椭圆C的离心率 .
 17. 平面向量满足 , 则的最小值为 .
17. 平面向量满足 , 则的最小值为 .三、解答题
-
18. 已知函数 .(1)、若的图像与直线相邻两个交点的距离为 , 求的值及的单调递增区间;(2)、当时,求函数在上的最大值.19. 如图,四棱锥中,平面 , 平面 , , F,M,N分别为的中点.
 (1)、求证:∥平面;(2)、求直线与平面所成角的正弦值.
(1)、求证:∥平面;(2)、求直线与平面所成角的正弦值.
