浙江省Z20名校联盟2022届高三下学期数学5月第三次联考试卷
试卷更新日期:2022-06-02 类型:高考模拟
一、单选题
-
1. 已知实数集 , 集合 , 则( )A、或 B、 C、或 D、2. 已知复数z满足(i为虚数单位),则复数z是( )A、 B、 C、 D、3. 已知实数、满足不等式组 , 则的最大值为( )A、13 B、11 C、9 D、74. 某几何体的三视图(单位:)如图所示,则该几何体的体积(单位:)为( )
 A、 B、32 C、 D、645. 设a,b都是不等于1的正数,则“”是“”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件6. 函数在区间上的图象大致是( )A、
A、 B、32 C、 D、645. 设a,b都是不等于1的正数,则“”是“”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件6. 函数在区间上的图象大致是( )A、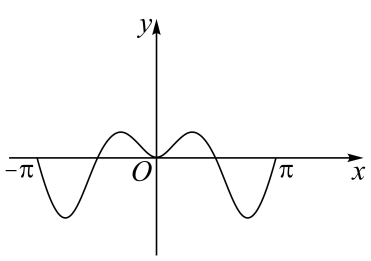 B、
B、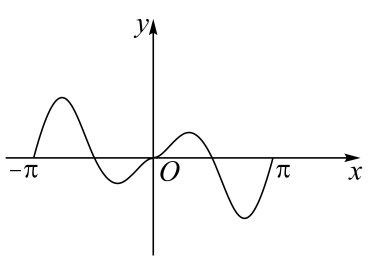 C、
C、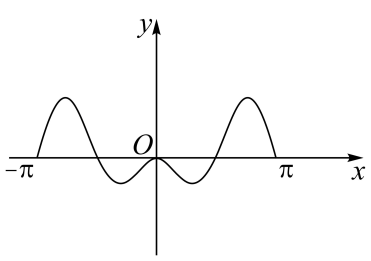 D、
D、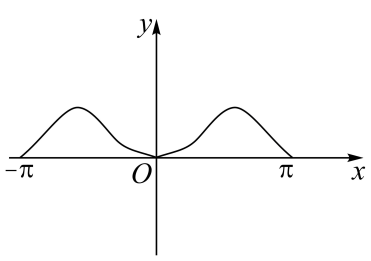 7. 随机变量的分布列如下所示,其中 , 则下列说法中正确的是( )
7. 随机变量的分布列如下所示,其中 , 则下列说法中正确的是( )-1
0
1
P
A、 B、 C、 D、8. 在正方体中,是线段(不含端点)上的点,记直线与直线成角为 , 直线与平面所成角为 , 二面角的平面角为 , 则( )A、 B、 C、 D、9. 已知函数 , 若对于任意的实数x,不等式恒成立,则实数a的取值范围为( )A、 B、 C、 D、10. 设数列满足 , 记数列的前n项的和为 , 则( )A、 B、存在 , 使 C、 D、数列不具有单调性二、填空题
-
11. 我国古代数学著作《增删算法统宗》中有这样一道题:“三百七十八里关,初行健步不为难;次日脚痛减一半,六朝才得到其关;要见每朝行里数,请君仔细详推算.”其大意为:“某人行路,每天走的路是前一天的一半,6天共走了378里.”则他第一天走了里路,前四天共走了里路.12. 已知函数 , 则;若 , 且 , 则 .13. 已知多项式 , 则 , .14. 在中,内角A的平分线与边交于点D,且 , 则;若 , , 则的取值范围是 .15. 已知实数 , 则的最小值为 .16. 已知双曲线的两个焦点分别为 , 点是双曲线第一象限上一点,在点P处作双曲线C的切线l,若点到切线l的距离之积为3,则双曲线C的离心率为 .17. 已知平面向量满足 , 设 , 若 , 则的取值范围为 .
三、解答题
-
18. 已知函数 .(1)、求的单调递增区间;(2)、若对任意 , 都有 , 求实数的取值范围.19. 如图,在四棱锥中, .
 (1)、若 , 证明:平面平面;(2)、若 , 求直线与平面所成角的正切值的最小值.20. 已知数列的前项和为 , 且满足 , , 数列满足 , , 其中 .(1)、求数列和的通项公式;(2)、设 , 求数列的前项和 .
(1)、若 , 证明:平面平面;(2)、若 , 求直线与平面所成角的正切值的最小值.20. 已知数列的前项和为 , 且满足 , , 数列满足 , , 其中 .(1)、求数列和的通项公式;(2)、设 , 求数列的前项和 .
