浙江省2022届高三下学期数学高考冲刺卷（二）

试卷更新日期：2022-06-02 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = {x \in N | x \leq 4}$ ，集合 $A = {1 ， m} ， B = {1 ， 2 ， 4}$ .若 $∁_{U} (A ∩ B) = {0 ， 2 ， 3}$ ，则 $m =$ （）

A、4 B、3 C、2 D、0

查看试题解析
2. 已知复数 $z$ 满足 $z \cdot (2 - i^{2}) = i + 1$ ，则共轭复数 $\bar{z}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知 $α ， β$ 是两个不同的平面，直线 $l ⊄ α$ ，且 $α ⊥ β$ ，那么“ $l / / α$ ”是“ $l ⊥ β$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 若一个几何体的三视图如图所示，则该几何体最长的棱长为（）

A、 $\sqrt{13}$ B、 $2 \sqrt{5}$ C、 $\sqrt{21}$ D、 $\sqrt{29}$

查看试题解析
5. 已知点 $P (x ， y)$ 满足不等式组 ${\begin{array}{l} 2 x - y \geq 0 ， \\ x + y - 2 \leq 0 ， \\ x - 2 y - 2 \leq 0 ， \end{array}$ ，点 $A (2 ， 1)$ ， $O$ 为坐标原点，则 $\vec{O P} \cdot \vec{O A}$ 的取值范围是（）

A、 $[- \frac{8}{3} ， \frac{8}{3}]$ B、 $[- \frac{8}{3} ， 4]$ C、 $[\frac{8}{3} ， 4]$ D、 $(- \infty ， - \frac{8}{3}]$

查看试题解析
6. 如图，S﹣ABC是正三棱锥且侧棱长为a，E，F分别是SA，SC上的动点，三角形BEF的周长的最小值为 $\sqrt{2} a$ ，则侧棱SA，SC的夹角为（）

A、30° B、60° C、20° D、90°

查看试题解析
7. 函数 $f (x) = x \lg (x^{2} + 1) + 2 x$ 的部分图象大致为（）

A、 B、 C、 D、

查看试题解析
8. 设函数 $f (x) = c o s (ω x + φ)$ ，其中 $ω > 0$ ，若对任意的 $φ \in [\frac{π}{6} ， \frac{π}{4}]$ ， $f (x)$ 在 $[0 ， 2 π]$ 上有且仅有4个零点，则下列 $ω$ 的值中不满足条件的是（）

A、 $ω = \frac{13}{6}$ B、 $ω = \frac{11}{6}$ C、 $ω = \frac{5}{4}$ D、 $ω = \frac{3}{4}$

查看试题解析
9. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左､右焦点分别为 $F_{1} ， F_{2}$ ， M为右支上一点， $∠ M F_{2} F_{1} = 120 ° ， △ M F_{1} F_{2}$ 的内切圆圆心为Q，直线 $M Q$ 交x轴于点N， $| M Q | = 2 | Q N |$ ，则双曲线的离心率为（）

A、 $\frac{5}{4}$ B、 $\frac{4}{3}$ C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
10. 已知数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， $a_{n} = a_{n - 1} + 4 (\sqrt{a_{n - 1}} + \frac{1}{\sqrt{a_{n - 1}}}) (n \in N^{*} ， n \geq 2)$ ， $S_{n}$ 为数列 ${\frac{1}{a_{n}}}$ 的前n项和，则（）

A、 $\frac{7}{3} < S_{2022} < \frac{8}{3}$ B、 $2 < S_{2022} < \frac{7}{3}$ C、 $\frac{5}{3} < S_{2022} < 2$ D、 $1 < S_{2022} < \frac{5}{3}$

查看试题解析

二、填空题

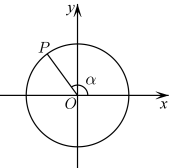
11. 如图所示，角 $α$ 的终边与单位圆交于点 $P$ ，已知点 $P$ 的坐标为 $(- \frac{3}{5} ， \frac{4}{5})$ ，则 $t a n 2 α =$ ．

查看试题解析
12. 已知 $f (x) = {\begin{array}{l} e^{x} + 1 ， x \leq 0 \\ f (x - 2) ， x > 0 \end{array}$ ，则 $f (3)$ 的值为．

查看试题解析
13. 若函数f(x)＝64x⁶表示为f(x)＝a₀＋a₁(2x－1)＋a₂(2x－1)²＋…＋a₆(2x－1)⁶ ，其中a₀ ， a₁ ， a₂ ， …，a₆为实数，则a₅＝， a₂＋a₄＋a₆＝.

查看试题解析
14. 已知 $△ A B C$ 中，角A，B，C所对的边分别是 $a, b, c$ ，已知 $a = 2, c = 5, B = 60^{\circ}$ ， $D$ 是边 $A C$ 上一点，且 $\sin ∠ A B D = \frac{\sqrt{3}}{3}$ ，则 $b$ =； $\frac{A D}{D C}$ =.

查看试题解析
15. 随机变量 $ξ$ 的分布列如下表，其中 $\frac{1}{4} \leq p \leq \frac{1}{2}$ ．当 $p =$ 时， $E (ξ)$ 取最小值；当 $p =$ 时， $D (ξ)$ 有最小值．
$ξ$
1
2
3
p
p
$\frac{1}{3}$
$\frac{2}{3} - p$

查看试题解析
16. 双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{4} = 1 (a > 0)$ 的左､右顶点分别为 $A ， B$ ，过点 $M (2 ， 0)$ 的直线 $l$ 交该双曲线 $C$ 于点 $P ， Q$ ，设直线 $P A$ 的斜率为 $k_{1}$ ，直线 $Q B$ 的斜率为 $k_{2}$ ，已知 $l ⊥ x$ 轴时， $\frac{k_{1}}{k_{2}} = - \frac{1}{3}$ ，则双曲线 $C$ 的离心率 $e =$ ；若点 $P$ 在双曲线右支上，则 $k_{2}$ 的取值范围是.

查看试题解析
17. 已知平面向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 满足 $\vec{a}$ 与 $\vec{b}$ 的夹角为锐角， $| \vec{a} | = 4$ ， $| \vec{b} | = 2$ ， $| \vec{c} | = 1$ ，且 $| \vec{b} + t \vec{a} |$ 的最小值为 $\sqrt{3}$ ，则实数 $t$ 的值是，向量 $(\vec{c} - \frac{1}{2} \vec{a}) \cdot (\vec{c} - \vec{b})$ 的取值范围是.

查看试题解析

三、解答题

18. 向量 $\vec{m} = (\sqrt{2} s i n x ， \frac{1}{2})$ ， $\vec{n} = (\frac{\sqrt{6}}{2} c o s x ， - \frac{3}{2})$ ，函数 $f (x) = \vec{m} \cdot (\vec{m} + 2 \vec{n})$ .

(1)、求函数 $f (x)$ 的对称中心；

(2)、若函数 $g (x) = f (x) + \frac{1}{4}$ 在 $[- \frac{π}{4} ， a]$ 上有5个零点，求 $a$ 的取值范围；

(3)、在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ， $∠ A C B$ 的角平分线交 $A B$ 于点 $D$ ，且 $f (C)$ 恰好为函数 $f (x)$ 的最大值.若此时 $C D = f (C)$ ，求 $4 a + 3 b$ 的最小值.

查看试题解析
19. 如图，在四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面四边形ABCD为菱形， $∠ A B C = 6 0^{∘} ， A A_{1} = A_{1} B_{1} = \frac{1}{2} A B = 1 ， A A_{1} ⊥$ 平面 $A B C D$ .

(1)、若点 $M$ 是 $A D$ 的中点，求证： $C_{1} M / /$ 平面 $A B B_{1} A_{1}$

(2)、求直线 $C_{1} M$ 与平面 $A D_{1} D$ 所成角的余弦值；

(3)、棱 $B C$ 上存在点 $E$ ，使得 $C E = 1 - \frac{\sqrt{3}}{2}$ ，求平面 $E A D_{1}$ 与平面 $A D_{1} D$ 的夹角的正弦值.

查看试题解析
20. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，点 $(a_{n} ， S_{n})$ 在直线 $2 x - y - n = 0$ 上 $(n \in N^{*})$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、记 $b_{n + 1} = a_{n} + b_{n} - \sqrt{{a_{n}}^{2} + {b_{n}}^{2}}$ ，数列 ${b_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，求使得 $T_{n} < \frac{2021}{2022}$ 成立的 $n$ 的最大值．

查看试题解析
21. 已知抛物线 $C$ ： $y^{2} = 2 p x$ 经过点 $P (1 ， m) (m > 0)$ ，焦点为F，PF=2，过点 $Q (0 ， 1)$ 的直线 $l$ 与抛物线 $C$ 有两个不同的交点 $A$ ， $B$ ，且直线 $P A$ 交 $y$ 轴于 $M$ ，直线 $P B$ 交 $y$ 轴于 $N$ ．

(1)、求抛物线C的方程

(2)、求直线 $l$ 的斜率的取值范围；

(3)、设 $O$ 为原点， $\vec{Q M} = λ \vec{Q O}$ ， $\vec{Q N} = μ \vec{Q O}$ ，求证： $\frac{1}{λ} + \frac{1}{μ}$ 为定值．

查看试题解析
22. 已知函数 $f (x) = x^{2} - (2 a + 6) x + 6 a l n x (a > 0)$ ．

(1)、若 $a = 1$ ，求函数 $f (x)$ 的单调递增区间；

(2)、（ⅰ）若 $x = 3$ 是函数 $f (x)$ 的极大值点，记函数 $f (x)$ 的极小值为 $g (a)$ ，求证： $g (a) < 7 - 2 a$ ；
（ⅱ）若 $h (x) = f (x) + x$ 在区间 $(0 ， + \infty)$ 上有两个极值点 $x_{1} ， x_{2} (x_{1} < x_{2})$ ．求证： $h (x_{2}) < 0$ ．（提示： $l n 4 < \frac{13}{9} ， l n 5 < \frac{5}{3} ， l n 7 < 2$ ）．

查看试题解析

$ξ$	1	2	3
p	p	$\frac{1}{3}$	$\frac{2}{3} - p$