浙江省绍兴市嵊州市三界片联考2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-06-01 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题2分，共20分）

1. 如图，直线a∥b，∠1＝120°，则∠2的度数是（）

A、120° B、80° C、60° D、50°

查看试题解析
2. 下列运算正确的是（）

A、a²•a³＝a⁶ B、a⁶÷a²＝a⁴ C、（3ab²）³＝9a³b⁶ D、（a³）²＝a⁵

查看试题解析
3. 下列各组数中，是二元一次方程5x﹣y＝2的一个解的是（）

A、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 0 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 0 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$

查看试题解析
4. 一个长方形的长为2x﹣y，宽为2x+y，则这个长方形的面积是（）

A、4x²﹣y² B、4x²+y² C、2x²﹣y² D、2x²+y²

查看试题解析
5. 如图，在下列给出的条件下，不能判定AB∥DF的是（）

A、∠A+∠2＝180° B、∠A＝∠3 C、∠1＝∠4 D、∠1＝∠A

查看试题解析
6. 如图，将一个直角三角板和一把直尺按如图所示摆放，若∠1＝35°，则∠2的度数为（）

A、35° B、45° C、50° D、55°

查看试题解析
7. 若（x﹣5）⁰＝1，则x的取值范围是（）

A、x＞5 B、x＜5 C、x≠5 D、一切实数

查看试题解析
8. 如果（x+1）（2x+m）的乘积中不含x的一次项，则m的值为（　　）

A、2 B、﹣2 C、0.5 D、﹣0.5

查看试题解析
9. 对x，y定义一种新运算“※”，规定：x※y＝mx+ny（其中m，n均为非零常数），若1※1＝4，1※2＝3．则2※1的值是（）

A、3 B、5 C、9 D、11

查看试题解析
10. 有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的面积之和为（）

A、11 B、12 C、13 D、14

查看试题解析

二、填空题（本大题共10小题，每小题3分，共30分）

11. 芝麻作为食品和药物均广泛使用，经测算，一粒芝麻重量约有0.00021kg，用科学记数法表示一粒芝麻的重量为 kg．

查看试题解析
12. 已知y﹣2x＝6，用含x的代数式表示y，则y＝．

查看试题解析
13. 计算16x⁵÷（8x）＝．

查看试题解析
14. 已知x^a＝3，x^b＝5，则x^a+b＝．

查看试题解析
15. 已知 ${\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ 是方程2x﹣ay＝3的一个解，那么a的值是．

查看试题解析
16. 如图，已知a，b，c，d四条直线，若∠1＝105°，∠2＝75°，∠3＝65°，则∠4＝度．

查看试题解析
17. 如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则CF的长为．

查看试题解析
18. 已知m+n＝2，mn＝﹣4，则（1﹣m）（1﹣n）＝．

查看试题解析
19. 已知x²﹣3x＝2，那么多项式x³﹣x²﹣8x+9的值是．

查看试题解析
20. 我国南宋时期杰出的数学家杨辉是钱塘人，如图是他在《详解九章算术》中记载的“杨辉三角”．此图揭示了（a+b）ⁿ（n为非负整数）的展开式的项数及各项系数的有关规律．

(1)、请仔细观察，填出（a+b）⁴的展开式中所缺的系数．
（a+b）⁴＝a⁴+4a³b+a²b²+4ab³+b⁴

(2)、此规律还可以解决实际问题：假如今天是星期一，再过7天还是星期一，那么再过8¹⁴天是星期．

查看试题解析

三、解答题

21. 计算：

(1)、2m•（mn）²；

(2)、（2⁵﹣1）⁰﹣（ $\frac{1}{3}$ ）^﹣¹；

(3)、 ${\begin{matrix} 3 x + 2 y = 9 \\ y = 7 - x \end{matrix}$ ；

(4)、 ${\begin{matrix} x - 3 y = 4 \\ 2 x + 3 y = - 1 \end{matrix}$ ．

查看试题解析
22. 先化简，再求值：（a+2）²﹣（a+1）（a﹣1），其中a $= - \frac{3}{2}$ ．

查看试题解析
23. △ABC在网格中的位置如图所示，请根据下列要求解答：

(1)、过点C作AB的平行线CD，其中要求点D是网格的格点；

(2)、A点经平移后到达A₁位置，请说明平移过程；

(3)、按照（2）的平移过程，作出△ABC经过平移后得到的△A₁B₁C₁；

(4)、连结AA₁ ， BB₁ ，请直接判断线段AA₁与线段BB₁的关系．

查看试题解析
24. 疫情防控期间，某学校为了增强学生体质，鼓励学生在不聚集的情况下加强体育锻炼，决定让各班购买跳绳和键子作为活动器材，已知购买2根跳绳和5个键子共需34元，购买4根跳绳和3个键子共需40元，求购买1根跳绳和1个键子分别需要多少元？

查看试题解析
25. 图①是一个长为2m，宽为2n（m＞n）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它平均分成形状和大小都一样的四块小长方形，然后按图②那样拼成一个正方形．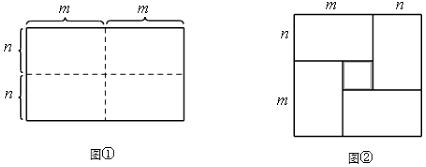

(1)、观察图②，请用两种不同的方法表示图②中阴影部分的面积：
方法1：；

方法2：；

(2)、直接写出三个代数式（m+n）² ，（m﹣n）² ， mn之间的等量关系：；

(3)、若a+b＝7，ab＝6，求a﹣b的值．

查看试题解析
26. 如图1，已知直线l₁∥l₂ ，且l₃和l₁、l₂分别相交于A、B两点，l₄和l₁、l₂分别交于C、D两点，∠ACP＝∠1，∠BDP＝∠2，∠CPD＝∠3．点P在线段AB上．

(1)、若∠1＝22°，∠2＝33°，则∠3＝．

(2)、试找出∠1、∠2、∠3之间的等量关系，并说明理由．

(3)、应用（2）中的结论解答下列问题：如图2，点A在B处北偏东40°的方向上，在C处的北偏西45°的方向上，求∠BAC的度数．

(4)、如果点P在直线l₃上且在A、B两点外侧运动时，其他条件不变，试探究∠1、∠2、∠3之间的关系（点P和A、B两点不重合），并证明其中的一种结论．

查看试题解析