浙江省杭州市上城区部分校2021-2022学年七年级下学期期中考试数学试卷

试卷更新日期：2022-06-01 类型：期中考试

进入出卷网下载

一、选择题（10小题，每题3分，共30分）

1. 下列生活现象中，属于平移的是（）

A、足球在草地上滚动 B、拉开抽屉 C、投影片的文字经投影转换到屏幕上 D、钟摆的摆动

查看试题解析
2. 方程组： ${\begin{cases} x + y = 5 ① \\ 2 x + y = 10 ② \end{cases}$ ，由②－①得到的方程是（）

A、3x＝10 B、x＝－5 C、3 x＝－5 D、x＝5

查看试题解析
3. 如图，下列说法错误的是（）

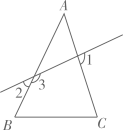A、∠C与∠1是内错角 B、∠2与∠A是内错角 C、∠A与∠B是同旁内角 D、∠A与∠3是同位角

查看试题解析
4. 下列运算正确的是（）

A、 ${(a + b)}^{3} = a^{3} + b^{3}$ B、 $2 a^{3} \cdot 3 a^{2} = 6 a^{6}$ C、 ${(- x^{3})}^{4} = x^{12}$ D、 ${(- x)}^{3 n} \div {(- x)}^{2 n} = - x^{n}$

查看试题解析
5. 已知：如图，直线a∥b，∠1＝50°.若∠2＝∠3，则∠2的度数为（）

A、50° B、60° C、65° D、75°

查看试题解析
6. 按下列程序计算，最后输出的答案是（）

A、 $a^{3}$ B、 $a^{2} + 1$ C、 $a^{2}$ D、 $a$

查看试题解析
7. 下列分解因式正确的是（）

A、 $x y - 4 = (x - 2) (y + 2)$ B、 $3 x - 6 y + 3 = 3 (x - 2 y)$ C、 $x^{2} - x - 2 = (x + 2) (x - 1)$ D、 $- x^{2} + 2 x - 1 = - {(x - 1)}^{2}$

查看试题解析
8. 已知 $a \neq c$ ，若M＝a²－ac，N＝ac－c² ，则M与N的大小关系是（）

A、M＞N B、M＝N C、M＜N D、不能确定

查看试题解析
9. 若 $x ， y$ 均为正整数，且 $2^{x + 1} \cdot 4^{y} = 128$ ，则 $x + y$ 的值为（）

A、4 B、5 C、4或5 D、无法确定

查看试题解析
10. 如图，AB∥CD，BF平分∠ABE，且BF⊥DE，垂足为F，则∠ABE与∠EDC的数量关系是（）

A、∠EDC－ $\frac{1}{2}$ ∠ABE＝90° B、∠ABE＋∠EDC＝180° C、∠ABE＝ $\frac{1}{4}$ ∠EDC D、∠ABE＋ $\frac{1}{2}$ ∠EDC＝90°

查看试题解析

二、填空题（6小题，每题4分，共24分）

11. 小数 0.00000025用科学记数法表示为.

查看试题解析
12. 分解因式：25a²－100＝．

查看试题解析
13. 如果将 $1 + 4 m^{2}$ 再加上一项，使它成为 ${(a + b)}^{2}$ 的形式（其中 $a \neq 0 ， b \neq 0$ ），那么可以加上的项为．（写出2个即可）

查看试题解析
14. 用“ $\otimes$ ”定义新运算：对于任意实数a，b，都有 $a \otimes b ＝ b^{2} ＋ 1$ .例如： $7 \otimes 4 ＝ 4^{2} ＋ 1 ＝ 17$ ，那么2022 $\otimes$ 5＝；当m为实数时， $m \otimes (m \otimes 2)$ ＝．

查看试题解析

15. 小明、小华和小芳三个人到文具店购买同一种笔记本和钢笔，他们把各自购买的数量和总价列成了表格．聪明的小明发现其中有一个人把总价算错了，这个算错的人是．

	小明	小华	小芳
笔记本(本)	15	24	27
钢笔(支)	25	40	45
总价(元)	330	528	585

查看试题解析

16. 如图，在边长为a(cm)的大正方形内放入三个边长都为b(cm)(a＞b)的小正方形纸片，这三张纸片没有盖住的面积是4cm² ，则a²－2ab＋b²的值为.

查看试题解析

三、解答题（共66分）

17. 计算：

(1)、 ${(\sqrt{3} - 2)}^{0} + {(- \frac{1}{2})}^{- 3}$

(2)、[(2x－y)(2x＋y)＋y(y－6x)]÷(2x)

查看试题解析
18. 解方程：

(1)、 ${\begin{cases} 3 x - 2 y = - 1 \\ x - y = 1 \end{cases}$ ；

(2)、 ${\begin{cases} x + 3 y = 2 \\ 3 x - 13 y = - 4 \end{cases}$ ．

查看试题解析
19. 如图，AD⊥AE，BC⊥AE，∠B＝∠D，点D，C，E在同一条直线上．

(1)、完成下面的说理过程．
∵AD⊥AE，BC⊥AE，(已知)

∴∠1＝90°，∠2＝90°，(垂直的定义)

∴∠1＝∠2，

∴AD∥BC，（）

∴∠D＝∠BCE，（）

又∠B＝∠D，

∴∠B＝∠BCE，

∴AB∥CD.（）

(2)、若∠BAD＝150°，求∠E的度数．

查看试题解析
20.

(1)、先化简 ${(2 x + 1)}^{2} - (2 x + 1) (2 x - 1) + (x + 1) (x - 3)$ ，并请选择你所喜欢的x的值代入求值．

(2)、方程组 ${\begin{matrix} x + y = 1 \\ k x + (k - 1) y = 7 \end{matrix}$ 的解 $x ， y$ 满足 $3 x - 2 y = 5$ ，求k的值.

查看试题解析
21. 某场篮球赛，门票共两种，价格分别为：成人票30元/张，儿童票10元/张．门票总收入为：6900元．

(1)、若售出门票总数290张，求售出的成人票张数．

(2)、设售出门票总数a张，其中儿童票b张．
①求a，b满足的数量关系．

②若售出的门票中成人票比儿童票的7倍还多10张，求b的值．

查看试题解析
22. 如图，AP，CP分别平分∠BAC，∠ACD，∠P＝90 $°$ ，设∠BAP＝α.

(1)、用α表示∠ACP；

(2)、求证：AB∥CD；

(3)、若AP∥CF，求证：FC平分∠DCE.

查看试题解析
23. 若x满足(9 $-$ x)(x $-$ 4)=4，求(9 $-$ x)² $+$ (x $-$ 4)²的值.
解：设9 $-$ x=a，x $-$ 4=b，则(9 $-$ x)(x $-$ 4)=ab=4，a $+$ b=(9 $-$ x) $+$ (x $-$ 4)=5
∴(9 $-$ x)² $+$ (x $-$ 4)²=a²+b²=(a+b)² $-$ 2ab=5²—2 $\times$ 4=17

请仿照上面的方法求解下面问题：

(1)、若x满足 $(x - 10) (x - 20) = 15$ ，求 ${(x - 10)}^{2} + {(x - 20)}^{2}$ 的值；

(2)、若x满足 ${(x - 2021)}^{2} + {(x - 2022)}^{2} = 33$ ，求 $(x - 2021) (x - 2022)$ 的值

(3)、已知正方形ABCD的边长为x，E，F分别是AD、DC上的点，且AE=1，CF=3，长方形 EMFD的面积是48，分别以MF，DF为边长作正方形MFRN和正方形GFDH，求阴影部分的面积.

查看试题解析