浙江省杭州市钱塘新区2022年中考数学模拟试卷
试卷更新日期:2022-06-01 类型:中考模拟
一、选择题(本大题共10小题,共30分)
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 如图是用五块小正方体搭建的积木,该几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. “大江大湖大武汉,好山好水好黄陂”2019年国庆假日,我区旅游市场规范繁荣,旅游热度持续不减,2019年10月1日至7日,全区共接待游客约210万人次,210万人次用科学记数法表示为( )A、 B、 C、 D、4. 不等式组 的解集是A、 B、 C、 D、5. 取一次函数 部分的自变量 值和对应函数 值如表:
3. “大江大湖大武汉,好山好水好黄陂”2019年国庆假日,我区旅游市场规范繁荣,旅游热度持续不减,2019年10月1日至7日,全区共接待游客约210万人次,210万人次用科学记数法表示为( )A、 B、 C、 D、4. 不等式组 的解集是A、 B、 C、 D、5. 取一次函数 部分的自变量 值和对应函数 值如表:-1
0
1
-3
-1
1
根据信息,下列说法错误的是( )
A、 B、当 时 C、 D、不等式 的解集是6. 甲、乙两人进行射击比赛,在相同条件下各射击10次,他们的平均成绩一样,而他们的方差分别是S甲2=1.8,S乙2=0.7,则成绩比较稳定的是( )A、甲稳定 B、乙稳定 C、一样稳定 D、无法比较7. 如图,直线 ,一等腰 的三个顶点 、 、 分别在直线 、 、 上, , 交 于点 若 与 的距离为 , 与 的距离为 ,则 的值是( ) A、 B、 C、 D、8. 一本书共280页,小颖要用14天把它读完,当她读了一半时,发现平均每天需多读21页才能恰好在规定的时间内读完,如果读前一半时,小颖平均每天读x页,则下列方程中正确的是( )A、 B、 C、 D、9. 抛物线 如图所示,下列结论中正确的有( )
A、 B、 C、 D、8. 一本书共280页,小颖要用14天把它读完,当她读了一半时,发现平均每天需多读21页才能恰好在规定的时间内读完,如果读前一半时,小颖平均每天读x页,则下列方程中正确的是( )A、 B、 C、 D、9. 抛物线 如图所示,下列结论中正确的有( ); ; ; ; 其中 是不等于 的实数 .
 A、1个 B、2个 C、3个 D、4个10. 如图,在菱形 中,对角线 与 交于点 , 是边 的中点,连结 若菱形 的面积为24, ,则 的长为
A、1个 B、2个 C、3个 D、4个10. 如图,在菱形 中,对角线 与 交于点 , 是边 的中点,连结 若菱形 的面积为24, ,则 的长为 A、 B、3 C、 D、5
A、 B、3 C、 D、5二、填空题(本大题共6小题,共18分)
-
11. 已知 为整数,且分式 的值为整数,则 可取的值有 个.12. 已知 ,则化简 后的值是.13. 一个袋中有形状材料均相同的白球2个红球4个,任意摸一个球是红球的概率.14. 在 中,直线 直线 于 ,直线 直线 于 ,直线 与 相交于点 ,若 , ,则 的度数等于.15. 圆心角为 、半径为6的弧长为 ;面积为 .16. 如图,正方形 , 的顶点 , , 在坐标轴上,点 在 上,点 , 在函数 的图象上,则:
 (1)、点 的坐标是;(2)、点 的坐标是.
(1)、点 的坐标是;(2)、点 的坐标是.三、解答题(本大题共7小题,共72分)
-
17. 字母 , , , 所表示的数如表:
字母
字母表示的数
4的平方根
的相反数
单项式 的系数
(1)、直接写出上表中各字母所表示的数;(2)、计算(1)中最大数与最小数的平方差.18. 学校某社团为了调査南岸区上新街市民上班时最常用的交通工具的情况,随机抽取了上新街部分市民进行调查,要求被调查者从“ :公交车”“ :家庭汽车”“ :地铁”“ :电动车”“ :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如图所示的不完整的条形统计图和扇形统计图,请结合统计图解答下列问题: (1)、表示 组的扇形统计图所对应的圆心角是▲ 度,补全条形统计图;(2)、若社团成员想从 组的甲、乙、丙、丁四人中随机选择两人,了解他们使用的电动车品牌情况,请用列表或画树状图的方法求出恰好选中乙的概率.19. 求证:如果一个三角形一个角的平分线与它一边上的中线重合,那么这个三角形是等腰三角形.20. 已知矩形的一边长为2,另一边长为1.(1)、是否存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍?小明是这样想的:小刚是这样想的:
(1)、表示 组的扇形统计图所对应的圆心角是▲ 度,补全条形统计图;(2)、若社团成员想从 组的甲、乙、丙、丁四人中随机选择两人,了解他们使用的电动车品牌情况,请用列表或画树状图的方法求出恰好选中乙的概率.19. 求证:如果一个三角形一个角的平分线与它一边上的中线重合,那么这个三角形是等腰三角形.20. 已知矩形的一边长为2,另一边长为1.(1)、是否存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的2倍?小明是这样想的:小刚是这样想的:
按照小明思路,完成解答:
根据小刚的思路,直接写出两个交点坐标;
(2)、如果存在另一个矩形,周长是已知矩形周长的2倍,面积是已知矩形面积的 倍 ,求 的取值范围.21. 如图,在直角梯形 中, , , , , ,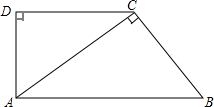 (1)、求证: ∽ ;(2)、求 的长.22. 已知:如图,抛物线 交 轴正半轴于点 ,负半轴于点 ,交 轴于点 , .
(1)、求证: ∽ ;(2)、求 的长.22. 已知:如图,抛物线 交 轴正半轴于点 ,负半轴于点 ,交 轴于点 , . (1)、求 值;(2)、点 为第一象限抛物线上一点,连接 、 、 ,若点 的横坐标为 , 的面积为 ,求 与 的函数解析式, 请直接写出自变量 的取值范围 ;(3)、在(2)的条件下,过点 作 轴交 延长线于点 ,连接 ,交 轴于点 ,点 为第二象限抛物线上一点,连接 并延长分别交 轴、抛物线于点 、 ,连接 ,交 轴于点 ,当 为 的中点且 时,求直线 的解析式.23. 机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)、求 值;(2)、点 为第一象限抛物线上一点,连接 、 、 ,若点 的横坐标为 , 的面积为 ,求 与 的函数解析式, 请直接写出自变量 的取值范围 ;(3)、在(2)的条件下,过点 作 轴交 延长线于点 ,连接 ,交 轴于点 ,点 为第二象限抛物线上一点,连接 并延长分别交 轴、抛物线于点 、 ,连接 ,交 轴于点 ,当 为 的中点且 时,求直线 的解析式.23. 机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上. (1)、求弦BC的长;(2)、求圆O的半径长.(本题参考数据:sin67.4°= ,cos67.4°= ,tan67.4°= )
(1)、求弦BC的长;(2)、求圆O的半径长.(本题参考数据:sin67.4°= ,cos67.4°= ,tan67.4°= )