浙江省杭州市临安区2022年中考数学模拟试
试卷更新日期:2022-06-01 类型:中考模拟
一、选择题(本大题共10小题,共30分)
-
1. 的相反数的倒数是( )A、 B、 C、 D、2. 已知 , ,则 等于( )A、8 B、12 C、24 D、253. 如图, 平分 , ,若 的面积为 ,则 的面积为( )
 A、 B、 C、 D、无法确定4. 点 , 在函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、5. 在 方格中,将图 中的图形甲平移后位置如图 所示,则图形甲的平移方法正确的是( )
A、 B、 C、 D、无法确定4. 点 , 在函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、5. 在 方格中,将图 中的图形甲平移后位置如图 所示,则图形甲的平移方法正确的是( ) A、先向左平移1格,再向下平移2格 B、先向右平移3格,再向下平移2格 C、先向右平移1格,再向下平移3格 D、先向右平移2格,再向下平移3格6. 如图,在平面直角坐标系中,点A1 , A2在x轴上,点B1 , B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2),分别以A1 , A2 , B1 , B2其中的任意两点与点O为顶点作三角形,所作三角形是等腰三角形的概率是( )
A、先向左平移1格,再向下平移2格 B、先向右平移3格,再向下平移2格 C、先向右平移1格,再向下平移3格 D、先向右平移2格,再向下平移3格6. 如图,在平面直角坐标系中,点A1 , A2在x轴上,点B1 , B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2),分别以A1 , A2 , B1 , B2其中的任意两点与点O为顶点作三角形,所作三角形是等腰三角形的概率是( ) A、 B、 C、 D、7. 如图, , 为边 上一点,以点 为圆心,2为半径作 ,交 边于 、 两点,则当 与 相切时, 等于( )
A、 B、 C、 D、7. 如图, , 为边 上一点,以点 为圆心,2为半径作 ,交 边于 、 两点,则当 与 相切时, 等于( ) A、4 B、3 C、2 D、18. 已知二次函数 的图象如图,分析下列四个结论:① ;② ;③ ;④ .其中正确的结论有( )
A、4 B、3 C、2 D、18. 已知二次函数 的图象如图,分析下列四个结论:① ;② ;③ ;④ .其中正确的结论有( )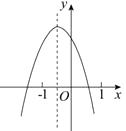 A、1个 B、2个 C、3个 D、4个9. 如图,矩形 ,两条对角线相交于 点,过点 作 的垂线 ,分别交 、 于 、 点,连结 ,若 , ,则 的长为( )
A、1个 B、2个 C、3个 D、4个9. 如图,矩形 ,两条对角线相交于 点,过点 作 的垂线 ,分别交 、 于 、 点,连结 ,若 , ,则 的长为( ) A、 B、 C、 D、10. 如图,是二次函数 的图象,图象经过点 ,二次函数的对称轴为 ,给出下列结论: ; ; ; ,其中正确的结论有( )
A、 B、 C、 D、10. 如图,是二次函数 的图象,图象经过点 ,二次函数的对称轴为 ,给出下列结论: ; ; ; ,其中正确的结论有( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18分)
-
11. 因式分解: .12. 一组数据:3,2,1,2,2的中位数是 , 方差是.13. 已知:如图,直线 ,将 按如图方式放置,其中点 在直线 上,点 在直线 上,若 ,则 的度数为.
 14. 如图, 经过 , , 三点, , 分别与 相切于 , 点, ,则 的度数为.
14. 如图, 经过 , , 三点, , 分别与 相切于 , 点, ,则 的度数为. 15. 如图,横、竖各12个方格,每个方格都有一个数,已知横行上任意3个相邻数之和为18,竖列上任意3个相邻数之和为20,图中已填入3、5、8和x四个数,那么x代表的数是.
15. 如图,横、竖各12个方格,每个方格都有一个数,已知横行上任意3个相邻数之和为18,竖列上任意3个相邻数之和为20,图中已填入3、5、8和x四个数,那么x代表的数是. 16. 已知 , , 平分 交 于点 , , , , ,则阴影部分的面积 即 与 的面积和 等于.
16. 已知 , , 平分 交 于点 , , , , ,则阴影部分的面积 即 与 的面积和 等于.
三、解答题(本大题共7小题,共72分)
-
17. 计算:(1)、 ;(2)、 .18. 为了了解某校对 中小学生每天一小时校园体育活动的规定 文件精神落实情况,随机调查了该校600名学生.调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,利用所得的数据制成了扇形统计图和频数分布直方图 部分未完成 根据图中信息,解答下列问题:
 (1)、在被调查的学生中随机选出一名学生,选出的是“每天锻炼超过1小时”的学生的概率是多少?(2)、在被调查的学生中“不喜欢”锻炼的人数是多少?并补全频数分布直方图.(3)、该校共有学生1200人,估计该校学生中每天锻炼未超过1小时的学生人数.19. ▱ ABCD 中, ∠BAD的平分线交直线 BC 于点 E,线 DC于点 F
(1)、在被调查的学生中随机选出一名学生,选出的是“每天锻炼超过1小时”的学生的概率是多少?(2)、在被调查的学生中“不喜欢”锻炼的人数是多少?并补全频数分布直方图.(3)、该校共有学生1200人,估计该校学生中每天锻炼未超过1小时的学生人数.19. ▱ ABCD 中, ∠BAD的平分线交直线 BC 于点 E,线 DC于点 F (1)、求证: ;(2)、若 , , ,求 .20. 如图,在平面直角坐标系中,已知一次函数 的图象与反比例函数 的图象交于点 .
(1)、求证: ;(2)、若 , , ,求 .20. 如图,在平面直角坐标系中,已知一次函数 的图象与反比例函数 的图象交于点 . (1)、求反比例函数的解析式;(2)、若一次函数 的图象与反比例函数 的图象的另一个交点为 ,请直接写出关于 的不等式 的解集.21. 如图,在矩形ABCD中,点E,F在对角线BD上,BE=DF请你判断: AE与CF的关系,并加以证明,(友情提示: 不要漏解! )
(1)、求反比例函数的解析式;(2)、若一次函数 的图象与反比例函数 的图象的另一个交点为 ,请直接写出关于 的不等式 的解集.21. 如图,在矩形ABCD中,点E,F在对角线BD上,BE=DF请你判断: AE与CF的关系,并加以证明,(友情提示: 不要漏解! )

