广西防城港市上思县2022年初中毕业班中考模拟数学试卷

试卷更新日期：2022-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的相反数是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列快递图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 不透明袋子中装有5个红球，3个绿球，这些球除了颜色外无其他差别，从袋子中随机摸出一个球，“摸出红球”的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{5}$ C、 $\frac{3}{5}$ D、 $\frac{5}{8}$

查看试题解析
4. 根据2021年6月2日公布的第七次人口普查数据，南宁市常住人口约为8740000，将8740000这个数用科学记数法表示为（）

A、 $87.4 \times 10^{5}$ B、 $8.74 \times 10^{6}$ C、 $874 \times 10^{4}$ D、 $0.874 \times 10^{7}$

查看试题解析
5. 在数轴上表示 $- 2 \leq x < 1$ 的解集，正确的是（）

A、 B、 C、 D、

查看试题解析
6. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(3 a)}^{3} = 9 a^{3}$ C、 $a^{3} + a^{3} = 2 a^{6}$ D、 $2 a \div a = 2 (a \neq 0)$

查看试题解析
7. 要反映中国在最近五届奥运会上获得的金、银、铜奖牌数量的变化情况，应选择（）

A、条形统计图 B、扇形统计图 C、折线统计图 D、以上都可以

查看试题解析
8. 将一副三角板按如图所示的位置摆放，则∠1的度数为（）

A、95° B、100° C、105° D、115°

查看试题解析
9. 如图，点P在双曲线 $y = \frac{k}{x}$ 第一象限的图象上， $P A ⊥ x$ 轴于点A，已知△OPA的面积为3，则k的值为（）

A、2 B、3 C、4 D、6

查看试题解析
10. 某车间有18名工人生产螺栓和螺母，每人每小时平均能生产螺栓24个或螺母36个，1个螺栓需要配2个螺母，若安排m名工人生产螺栓时每小时生产的螺栓和螺母刚好配套，那么可列方程为（）

A、24×m=36×（18-m）×2 B、24×（18-m）=36×m×2 C、24×m×2=36×（18-m） D、24×（18-m）×2=36×m

查看试题解析
11. 如图，小颖身高为 $160 c m$ ，在阳光下影长 $A B = 240 c m$ ，当她走到距离墙角（点 $D$ ） $120 c m$ 的 $C$ 处时，她的部分影子投射到墙上，则投射在墙上的影子 $D E$ 的长度为（）

A、 $120 c m$ B、 $80 c m$ C、 $60 c m$ D、 $40 c m$

查看试题解析
12. 如图，在矩形ABCD中，AD=5，AB=3 $\sqrt{3}$ ，点E在AB上， $\frac{AE}{EB}$ = $\frac{1}{2}$ ，在矩形内找一点P，使得∠BPE=60°，则线段PD的最小值为（）

A、4 B、2 $\sqrt{3}$ C、2 $\sqrt{7}$ -2 D、2 $\sqrt{13}$ -4

查看试题解析

二、填空题

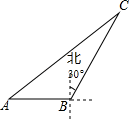
13. 二次根式 $\sqrt{x + 9}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
14. 把多项式 $a x^{2} - 4 a x + 4 a$ 因式分解的结果是.

查看试题解析
15. 小红参加学校举办的“我爱我的祖国”主题演讲比赛，她的演讲内容、演讲能力、演讲效果得分分别为86分，72分，81分，若依次按照40%，30%，30%的百分比确定成绩，则她的平均成绩是分.

查看试题解析
16. 如图，海中一渔船在A处与小岛C相距70海里，若该渔船由西向东航行30海里到达B处，此时测得小岛C位于B的北偏东30°方向上，则该渔船此时与小岛C之间的距离是海里.

查看试题解析

17. 请阅读下列材料，解答问题：

克罗狄斯·托勒密（约90年—168年），是希腊数学家，天文学家，地理学家和占星家.在数学方面，他还论证了四边形的特性，即有名的托勒密定理.

托勒密定理：圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.

如图，正五边形ABCDE内接于 $⊙ O$ ， $A B = 2$ ，则对角线BD的长为.

查看试题解析

18. 以矩形OABC的顶点O为坐标原点建立平面直角坐标系，使点A、C分別在x、y轴的正半轴上，双曲线 $y = \frac{k}{x} (k > 0)$ 的图象经过BC的中点D，且与AB交于点E，过OC边上一点F，把△BCF沿直线BF翻折，使点C落在矩形内部的一点 $C^{'}$ 处，且 $C^{'} E ∥ B C$ ，若点 $C^{'}$ 的坐标为（2，4），则直线BF的解析式为.

查看试题解析

三、解答题

19. 计算： $| - 1 | + 2 \times 3^{2} \div (1 - 4)$ .

查看试题解析
20. 先化简再求值： $(1 + \frac{1}{x - 1}) \cdot \frac{x^{2} - 1}{x}$ ，其中 $x = \sqrt{3} - 1$ .

查看试题解析
21. 如图，在Rt△ABC中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ 于点D.

(1)、作斜边AB上的中线CE，交AB于点E；（要求：尺规作图，保留作图痕迹，不必写作法和证明）

(2)、在（1）的条件下，已知 $B C = 2$ ， $B D = 1$ ，求CE的长.

查看试题解析
22. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害，为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民，就骑电瓶车戴安全帽情况进行问卷调查，将收集的数据制成如下统计图表.

活动前骑电瓶车戴安全帽情况统计表

类别

人数

A

68

B

245

C

510

D

177

合计

1000

(1)、宣传活动前，在抽取的市民中哪一类别的人数最多？占抽取人数的百分之几？

(2)、该市约有30万人使用电瓶车，请估计活动前全市骑电瓶车“都不戴”安全帽的总人数；

(3)、小明认为，宣传活动后骑电瓶车“都不戴”安全帽的人数为178，比活动前增加了1人，因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理？请结合统计图表，对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.

查看试题解析
23. 如图，Rt△ABC中， $∠ B A C = 90 °$ ，AB是 $⊙ O$ 的直径，BC与 $⊙ O$ 交于点D，连接AD，点F是圆上任意一点，连接AF，延长线交BC于点E， $∠ C A E = ∠ E B F$ .

(1)、求证： $A B = B E$ ；

(2)、若 $\tan C = \frac{3}{4}$ ， $A B = 5$ ，求EF的长.

查看试题解析
24. 综合与实践
【问题背景】

如图1，矩形 $A B C D$ 中， $A B = 10 ， B C = 8$ .点E为边 $B C$ 上一点，沿直线 $D E$ 将矩形折叠，使点C落在 $A B$ 边的点 $C^{'}$ 处.

(1)、【问题解决】
填空： $A C^{'}$ 的长为.

(2)、如图2，将 $△ D C^{'} E$ 沿线段 $A B$ 向右平移，使点 $C^{'}$ 与点B重合，得到 $△ D^{'} B E^{'} ， D^{'} E^{'}$ 与 $B C$ 交于点F， $D^{'} B$ 与 $D E$ 交于点G.求 $E F$ 的长；

(3)、【拓展探究】
在图2中，连接 $G F ， E E^{'}$ ，则四边形 $G E E^{'} F$ 是平行四边形吗？若是，请予以证明；若不是，请说明理由.

查看试题解析
25. R0，也叫基本传染数，或者基本再生数，英文为Basic reproduction number.更确切的定义是：在没有外力介入，所有人都没有免疫力的情况下，一个感染某种传染病的人，总共会传染给其他多少个人的平均数.最近，新型冠状病毒变异出德尔塔＋毒株，德尔塔＋变异病毒的R0值极高.若1人患病，在无任何外力影响下经历两轮传染后共有73人感染.

(1)、求德尔塔＋变异病毒的R0值；

(2)、国家研制出新冠疫苗后发现，通过接种疫苗可以使得R0值随接种人数比例的增高同步降低.例如，当疫苗全民接种率达到40%时，此时的R0值也下降40%.若有1人感染德尔塔＋变异病毒，要在两轮内将总感染人数控制在7人以内，再加以隔离等措施的干涉，就可控制住疫情，则全民接种率至少应该达到多少？

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = \frac{1}{3} x^{2} - 2 x$ 经过坐标原点，与x轴正半轴交于点A，该抛物线的顶点为M，直线 $y = - \frac{1}{2} x + b$ 经过点A，与y轴交于点B，连接 $O M$ .

备用图

(1)、求b的值及点M的坐标；

(2)、将直线 $A B$ 向下平移，得到过点M的直线 $y = m x + n$ ，且与x轴负半轴交于点C，取点 $D (2 ， 0)$ ，连接 $D M$ ，求证： $∠ A D M - ∠ A C M = 45 °$ ：

(3)、点E是线段 $A B$ 上一动点，点F是线段 $O A$ 上一动点，连接 $E F$ ，线段 $E F$ 的延长线与线段 $O M$ 交于点G.当 $∠ B E F = 2 ∠ B A O$ 时，是否存在点E，使得 $3 G F = 4 E F$ ？若存在，求出点E的坐标；若不存在，请说明理由.

查看试题解析

类别	人数
A	68
B	245
C	510
D	177
合计	1000