广西北部湾经济区2022年初中学业水平数学科模拟测试试卷
试卷更新日期：2022-06-01 类型：中考模拟
一、单选题
-
1. 下列图形中，不是中心对称图形的是（ ）A、
B、
C、
D、
2. 据羊城晚报消息，11 月 9 日，电影《长津湖》在官方微博发布海报，宣布该片票房突破 5 600 000000 元，已位居中国影史票房榜亚军.将数据 5 600 000 000 用科学记数法可表示为（ ）A、56×108 B、0.56×1010 C、5.6×109 D、5.6×10103. 掷一枚质地均匀的硬币，前 2021 次都是正面朝上，掷第 2022 次时反面朝上的概率是（ ）A、0 B、 C、 D、14. 如图，AB 是⊙O 的直径， ∠D＝32° ，则∠AOC 等于（ ）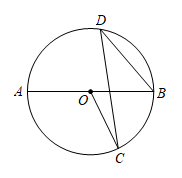
A、158° B、58° C、64° D、116°5. 下列变形正确的是（ ）A、由 3x＝4 得x ＝ B、由 a＞b 得 ac＞bc C、－2(x－3)＝－2x＋6 D、由 ＋2＝ 得 3＋2＝x6. 下列计算正确的是（ ）A、(2xy2)3＝8x3y6 B、x3＋x3＝2x6 C、x3 ·x3＝2x6 D、(x＋y)2＝x2＋y27. 为了解初三学生的体育锻炼时间，小华调查了某班45名同学一周参加体育锻炼的情况，并把它绘制成折线统计图（如图所示）.那么关于该班45名同学一周参加体育锻炼时间的说法错误的是（ ）
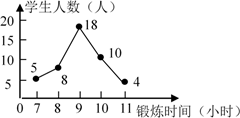A、众数是9 B、中位数是9 C、平均数是9 D、锻炼时间不低于9小时的有14人8. 如图，在教室前面墙壁 A 处安装了一个摄像头，当恰好观测到后面墙壁与底面交接处点 C 时，摄像头俯角约为 17°，受安装支架限制，摄像头观测的俯角最大约为 54° ，已知教室的长 (教室前后墙壁之间的距离 BC 的值) 是 9米，若摄像头与安装的墙壁之间距离忽略不计，则摄像头安装点高度 AB 约为（ ）米.(sin17° ≈ 0.29，tan17° ≈ 0.30，sin54° ≈ 0.8 ，tan54° ≈ 1.33，精确到 0.1 米) .
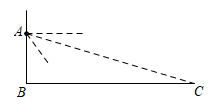A、2 B、2.7 C、3 D、3.29. 如图，AB∥CD∥EF，AF 与 BE 相交于点 G ，且 DG＝2 ，DF＝10 ， ＝ ，则 AG 的长为（ ）
A、2 B、3 C、4 D、510. 如图，将⊙O 沿弦 AB 折叠，被折叠后的一段弧正好经过圆心 O ，若 AB＝4 ，则图中阴影 部分的面积为（ ）
A、 π－4 B、 π＋8 C、 π＋4 D、8π－811. 我国古代数学著作《九章算术》中有这样一个问题：“今有方池一丈，葭生其中央，出水一 尺，引葭赴岸，适与岸齐.水深、葭长各几何？ ”.其大意是：如图，有一个水池，水面是 一个边长为 10 尺 (丈、尺是长度单位，1 丈＝10 尺) 的正方形，在水池正中央有一根芦苇， 它高出水面 1 尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面.水 的深度与这根芦苇的长度分别是多少？若设这跟芦苇的长度为 x 尺，根据题意，所列方程正 确的是（ ）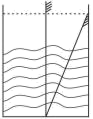
A、102＋(x－1)2＝x2 B、102＋(x－1)2 ＝ (x＋1)2 C、52＋(x－1)2＝x2 D、52＋(x－1)2 ＝ (x＋1)212. 如图，直线y＝－ x＋3 交 x 轴于点A ，交y 轴于点 B ，点 C 是y 轴的负半轴上的点，点 C、D 关于直线 AB 对称，连接 CD，交 AB 于点 E，交 x 轴于点 F，连接 AD、BD，双曲线 (x＞0) 恰好经过点 D .若∠BAD＝45°，则 k 的值为（ ）
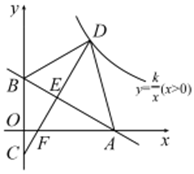A、27 －27 B、6 ＋6 C、18 D、12二、填空题
-
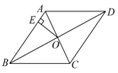
13. 在平面直角坐标系中点A (2 ，1) 关于y 轴对称点的坐标是.14. 因式分解：2ax2－2ay2＝.15. 已知地球表面陆地面积与海洋面积的比约为 3 ∶7，如果宇宙中飞来一块陨石落在地球上，那么这块陨石落在海洋里的概率约为.16. 如图，在菱形 ABCD 中，对角线 AC 与 BD 交于点 O ，OE⊥AB ，垂足为 E ，若 AE＋AD＝6 ，tan∠ADB＝1 ∶2 ，则菱形 ABCD 的面积为.
17. 星期六，王力上午 8：00 从家里出发，骑车到图书馆去借书，再骑车回到家.他离家的距离y(单位：千米) 与时间t(单位：分钟)的关系如图所示，则上午 8 ：45 王力离图书馆 千米.
18. 图所示，在半径为 6 的扇形 ABC 中， ∠BAC＝60° ，点 D ，E 分别在半径 AB，AC 上，且BD＝CE＝2，点F 是弧BC 上的动点，连接DF，EF，则DF＋ EF 的最小值为.
三、解答题
-
19. 计算： .20. 解不等式组： ，并把它的解集在数轴上表示出来.
21. 如图，在平面直角坐标系中，已知点A (－2 ，－5) 、B(－3 ，－1) 、C(－5 ，－4) .
⑴画出将△ABC 向上平移6个单位长度后对应的△A1B1C1；
⑵以点 O 为位似中心， 为位似比，在第一象限内，画出△ABC 的位似图形△A2B2C2；
⑶点 M 是 BC 的中点，请直接写出点 M 分别在△A1B1C1和△A2B2C2中的对应点 M1和 M2 的坐标.
22. 在建党 100 周年之际，为响应习总书记“学史明理”的号召，某市将开展以“争先锋学党史”为主题的知识竞赛活动，某校对 100 名参加选拔赛的同 学的成绩按 A ，B ，C，D 四个等级进行统计，绘制成如下不完整的统计表和扇形统计图：
成绩等级
频数/人
频率
A
5
0.05
B
m
0.52
C
n
D
合计
100
1
(1)、填空：m ＝ ， n ＝；(2)、在扇形统计图中，求“D 等级”所对应圆心角的度数；(3)、成绩等级为 A 的 5 名同学中有2名男生和3名女生，现从中随机挑选 2 名 同学代表学校参加全市比赛，请用树状图法或者列表法求出恰好选中“两名同性别选手”的概率.23. 如图，在平行四边形ABCD 中，AE 平分∠BAD且交BC于点E，连接DE，CE＝3，BE＝4，DE＝5.
(1)、求证：四边形 ABCD是矩形；(2)、连接BD交AE于点F，求△ADF的面积.24. 果汁厂现要从果商处购买荔枝和火龙果两种水果运回工厂，为了保证水果 新鲜，整个运输过程需要配置冷柜，荔枝的冷柜使用单价是火龙果的 ，运输过程中荔枝和 火龙果的冷柜费用分别是 3000 元和 800 元，且荔枝的数量比火龙果的多 20 吨.
(1)、求荔枝和火龙果的冷柜使用单价各是多少元/吨？(2)、现运输公司有大小两种车可供选择，已知一辆大车一次可运 4 吨，一辆小车一次可运 3 吨，在每辆车都装满且一次运完所有水果的情况下，有多少种租车方案？(3)、若同时用 2 吨荔枝和 0.6 吨火龙果可制成 1 吨果汁，果汁厂将制成的全部果汁运到经销 商处销售，如图，蓝天果汁厂与经销商处有公路和铁路相连，公路里程为 200 km ，铁路 里程不少于公路里程的 1.5 倍，运输过程还需要配置与荔枝同样单价的冷柜保鲜. 已知 公路运价为 1.5 元/ (吨 ·千米) ，铁路运价为 1 元/ (吨 ·千米) ，那么该果汁厂将全 部果汁运往经销商处的总费用最少是多少元？25. 如图 1 ，在等腰△ABC 中，AB＝AC，AO 平分∠BAC 且交 BC 于点 O，AB 与⊙O 相切于点 D ，OC 交⊙O 于点 H，连接 OD.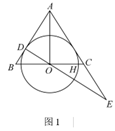
(1)、求证：AC 是⊙O 的切线；(2)、延长 DO 、AC 交于点 E ，若 CE＝OC，求证：OA＝OE；(3)、在 (2) 的条件下，连接 DH 交 AO 于点 K，如图2，若 OK ·AK＝8 －12 ，求⊙O 的半径并直 接写出 DK ·HK 的值.
26. 在平面直角坐标系中，已知抛物线 ：y＝a 与 ：y＝2a ，如图 1 所示， 点 A 的坐标为 (0 ，－6) ，过点 A 的线段 BC 平行于 x 轴，交抛物线 ：y＝a 的图象于点 B， 点 C(点 B 在点 C 的左侧) ，BC＝12.
(1)、求抛物线 L1 与 L2 的解析式；(2)、若点 D 是抛物线 L2 在第三象限上的点，若以 B，C，D为顶点的三角形是直角三角形， 请求出点 D 的坐标；(3)、如图 2，⊙A 的半径为 3，其切线 EF 交抛物线 L2 于点F，点 E 是切点，在第四象限内是否存在点 F，使 EF 的长度最小？若存在，请直接写出其最小值及此时点 F 的坐标；若不存在，请说明理由.