河南省南阳市镇平县2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-06-01 类型：期中考试

进入出卷网下载

一、单选题

1. 若代数式 $\frac{x}{x - 3}$ 的值为零，则实数x的值为（）

A、x＝0 B、x≠0 C、x＝3 D、x≠3

查看试题解析
2. 下列各点中，在第一象限内的点是（）

A、 $(- 5 ， - 3)$ B、 $(- 5 ， 3)$ C、 $(5 ， - 3)$ D、 $(5 ， 3)$

查看试题解析
3. 已知 $a = 2^{- 2}$ ， $b = {(- 1)}^{0}$ ， $c = {(- 1)}^{3}$ ，则a，b，c的大小关系是（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > a > b$ D、 $b > c > a$

查看试题解析
4. 如图，点B是反比例函数 $y = \frac{k}{x}$ （k≠0）在第一象限内图象上的一点，过点B作BA⊥x轴于点A，BC⊥y轴于点C，矩形AOCB的面积为6，则k的值为（　　）

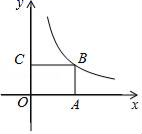A、3 B、6 C、﹣3 D、﹣6

查看试题解析
5. 纳米是非常小的长度单位，1纳米=10^﹣9米^.。某种病菌的长度约为50纳米，用科学记数法表示该病菌的长度，结果正确的是（）

A、5×10^﹣10米 B、5×10^﹣9米 C、5×10^﹣8米 D、5×10^﹣7米

查看试题解析
6. 已知反比例函数 $y = \frac{m - 2}{x}$ ，当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大，则 $m$ 的取值范围是（）

A、 $m < 2$ B、 $m > 2$ C、 $m \leq 2$ D、 $m \geq 2$

查看试题解析
7. 下列各式中，正确的是（）

A、 $\frac{x^{6}}{x^{2}} = x^{3}$ B、 $\frac{x + m}{x + n} = \frac{m}{n}$ C、 $\frac{x^{2} - 1}{x + 1} = x - 1$ D、 $\frac{x + y}{x - y} = - 1$

查看试题解析
8. 如图，已知正比例函数 $y_{1} = a x$ 与一次函数 $y_{2} = \frac{1}{2} x + b$ 的图象交于点P.下面有四个结论：① $a < 0$ ；② $b < 0$ ；③当 $x > 0$ 时， $y_{1} < 0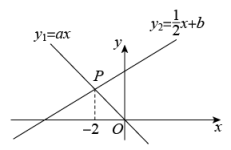$ ；④当 $x < - 2$ 时， $y_{1} < y_{2}$ .其中正确的是（）

A、①② B、②③ C、①③ D、①④

查看试题解析
9. 如果 $a - b = 1$ ，那么代数式 $(1 - \frac{b^{2}}{a^{2}}) \cdot \frac{2 a^{2}}{a + b}$ 的值是

A、2 B、-2 C、1 D、-1

查看试题解析
10. 如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x， $P A - P E = y$ ，图2是点P运动时y随x变化的关系图象，根据题意，下列说法错误的是（）

A、 $P A - P E \leq A E$ B、 $A B - B E = 1$ C、 $A E = 5$ D、PA最大时y值最大

查看试题解析

二、填空题

11. 计算： ${(π - 5)}^{0} + \sqrt{4} - | - 3 | =$ .

查看试题解析
12. 将直线y=x图象沿y轴向上平移2个单位长度后，所得直线的函数表达式为.

查看试题解析
13. 写出一个函数的表达式，使它满足：①图象经过点(1，1)；②在第一象限内函数y随自变量x的增大而减少，则这个函数的表达式为.

查看试题解析
14. 如果 $a^{2} + a - 3 = 0$ ，那么代数式 $(a + \frac{2 a + 1}{a}) \cdot \frac{a^{2}}{a + 1}$ 的值是．

查看试题解析
15. 如图，已知OD为等边△OAC的高，顶点 $O (0 ， 0)$ ， $D (1 ， 1)$ ，若△OAC绕点O逆时针旋转，每秒旋转45°，则第60秒时，D点坐标为.

查看试题解析

三、解答题

16. 如图，在平面直角坐标系中，函数 $y = x$ 的图象l是第一、三象限的角平分线.

(1)、实验与探究：由图观察易知 $A (0 ， 2)$ 关于直线l的对称点 $A^{'}$ 的坐标为 $(2 ， 0)$ ，请在图中分别标明 $B (5 ， 3)$ 、 $C (- 2 ， 5)$ 关于直线l的对称点 $B^{'}$ 、 $C^{'}$ 的位置，并写出它们的坐标；

(2)、归纳与发现：结合图形观察以上三组点的坐标，请你直接写出坐标平面内任一点 $P (m ， n)$ 关于第一、三象限的角平分线l的对称点 $P^{'}$ 的坐标.

查看试题解析
17. 先化简： $（ a - \frac{2 a - 1}{a}) \div \frac{1 - a^{2}}{a^{2} + a}$ ，然后从0，1，2中选一个你认为合适的a值，代入求值.

查看试题解析
18. 已知一次函数 $y = k x + b$ ，当 $x = 2$ 时y的值为1，当 $x = - 1$ 时y的值为-5.

(1)、在所给的平面直角坐标系中画出一次函数 $y = k x + b$ 的图象；

(2)、求k，b的值；

(3)、直接写出函数图象与x轴，y轴的交点坐标.

查看试题解析
19. 解方程：

(1)、 $\frac{3 x}{x + 2} + \frac{2}{x - 2} = 3$ ;

(2)、 $\frac{4}{x^{2} - 1} + \frac{x + 2}{1 - x} = - 1$ .

查看试题解析
20. 已知：反比例函数 $y = \frac{k}{x}$ 的图象经过 $A (2 ， - 4)$ .

(1)、求k的值；

(2)、这个函数的图象在哪几个象限？y随x的增大怎样变化？

(3)、画出函数的图象；

(4)、点 $B (- 2 ， 4)$ ， $C (- 1 ， 5)$ 在这个函数的图象上吗？

查看试题解析
21. 某工厂计划在规定时间内生产24000个零件，若每天比原计划多生产30个零件，则在规定时间内可以多生产300个零件．求原计划每天生产的零件个数和规定的天数．

查看试题解析
22. 如图，一次函数y=kx＋b的图象与反比例函数 $y = \frac{m}{x}$ 的图象相交于A、B两点，

(1)、利用图中条件，求反比例函数和一次函数的解析式

(2)、根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.

查看试题解析

23. 某游泳馆每年夏季推出两种游泳付费方式.方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元.设小明计划今年夏季游泳次数为x（x为正整数）.

(1)、根据题意，填写下表：

游泳次数	10	15	20	…	x
方式一的总费用（元）	150	175		…
方式二的总费用（元）	90	135		…

(2)、若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？

(3)、设方式一的总费用与方式二的总费用的差为y元.

①求y与x之间的函数关系式；

②小明选择哪种方式比较合算？

查看试题解析