甘肃省兰州市教育局第四片区2021-2022学年八年级下学期期中考试数学试卷

试卷更新日期：2022-06-01 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $x > y$ ，则下列不等式一定成立的是（）.

A、 $x - 6 < y - 6$ B、 $3 x < 3 y$ C、 $- 2 x < - 2 y$ D、 $2 x + 1 < 2 y + 1$

查看试题解析
2. 下列图形中，既是轴对称又是中心对称的图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列式子从左边到右边的变形中，是分解因式的是（）

A、 $x^{2} - x + 2 = x (x - 1) + 2$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 $m^{2} - m + \frac{1}{4} = {(m - \frac{1}{2})}^{2}$ D、 $x^{2} + 3 x + 2 = x (x + 3 + \frac{2}{x})$

查看试题解析
4. 如图，△ABC是等边三角形，且AD=BE=CF，则△DEF是（）

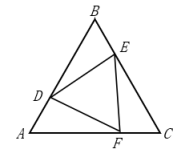A、等边三角形 B、等腰三角形 C、钝角三角形 D、直角三角形

查看试题解析
5. 如图，四边形ABCD中，∠B＝∠D＝90°，添加下列条件后仍不能判定△ABC与△ADC全等的是（　　）

A、AB＝AD B、∠ACB＝∠CAD C、AB＝BC D、∠BAC＝∠DAC

查看试题解析
6. 某校学生会组织七年级和八年级共60名同学参加环保活动，七年级学生平均每人收集15个废弃塑料瓶，八年级学生平均每人收集20个废弃塑料瓶．为了保证所收集的塑料瓶总数不少于1000个，至少需要多少名八年级学生参加活动？设需要x名八年级学生参加活动，则下列不等式正确的是（）

A、 $15 (60 - x) + 20 x \geq 1000$ B、 $15 (60 - x) + 20 x > 1000$ C、 $15 x + 20 (60 - x) \geq 1000$ D、 $15 x + 20 (60 - x) > 1000$

查看试题解析
7. 如图，将△ABC沿直线AB向右平移后到达△BDE的位置，连接CD、CE，若△ACD的面积为8，则△BCE的面积为（）

A、5 B、6 C、10 D、4

查看试题解析
8. 把 $2 x y - x^{2} - y^{2}$ 分解因式，结果正确的是（）.

A、 ${(x - y)}^{2}$ B、 ${(- x - y)}^{2}$ C、 $- {(x - y)}^{2}$ D、 $- {(x + y)}^{2}$

查看试题解析
9. 如图，在△ABC中，AD平分∠BAC，DE⊥AB于E， $S_{△ ABC}$ =15，DE=3，AB=6，则AC长是（）

A、4 B、5 C、6 D、7

查看试题解析
10. 如图，可以得出不等式组 ${\begin{array}{l} a x + b > 0 \\ c x + d < 0 \end{array}$ 的解集是（）

A、 $x < 4$ B、 $x < - 1$ C、 $- 1 < x < 0$ D、 $- 1 < x < 4$

查看试题解析
11. 在△ABC中，若三边长 $a ， b ， c$ 满足 $a^{2} + 2 a b + b^{2} = c^{2} + 24$ ， $a + b - c = 4$ ， △ABC的周长是（）

A、12 B、16 C、8 D、6

查看试题解析
12. 如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连接CE交AD于点F，连接BD交CE于点G，连接BE．下列结论中，正确的结论有（）
①CE＝BD；②△ADC是等腰直角三角形；③∠ADB＝∠AEB；④S_四_边_形BCDE＝ $\frac{1}{2}$ BD•CE；⑤BC²+DE²＝BE²+CD² ．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分解因式： $2 x^{2} - 8$ = ．

查看试题解析
14. 不等式 $- 2 x - 3 < 4$ 的解集为：．

查看试题解析
15. 如图，在△ABC中，EF是AB的垂直平分线，与AB交于点D，BF＝4，CF＝1，则AC的长为．

查看试题解析
16. 如图，△ABC中，∠ACB＝90°，把△ABC绕点C顺时针旋转到△A₁B₁C的位置，A₁B₁交直线CA于点D．若AC＝6，BC＝8，当线段CD的长为时，△A₁CD是等腰三角形．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 3 x - 1 > 5 \\ 2 x < 6 \end{array}$

查看试题解析
18. 分解因式： $\frac{x^{2}}{4} + x y + y^{2}$

查看试题解析
19. 如图，平面直角坐标系中，△ABC三个顶点的坐标分别为A（﹣3，5），B（﹣5，3），C（﹣2，2）平移到△A₁B₁C₁ ，其中点A的对应点A₁的坐标为（3，3）．

（1）请在图中画出△A₁B₁C₁；
（2）若将△ABC到△A₁B₁C₁的过程看成两步平移，请描述平移过程：；
（3）已知△A₁B₁C₁与△A₂B₂C₂关于原点O中心对称，请在图中画出△A₂B₂C₂ ，此时△A₂B₂C₂与△ABC关于某点中心对称这一点的坐标为．

查看试题解析
20. 已知：如图，∠CAE是△ABC的外角，AD∥BC且∠1＝∠2，求证：AB＝AC．

查看试题解析
21. 已知： $a + b = - 2$ ， $a b = 1$ ，求下列多项式的值．

(1)、 $a^{2} - 2 a b + b^{2} - 2$

(2)、 $4 a^{2} b + 4 a b^{2} - 4 a - 4 b$

查看试题解析
22. 如图，在Rt△ABC中，∠C=90°，∠A=33°，将△ABC沿AB方向向右平移得到△DEF．

(1)、试求出∠E的度数；

(2)、若AE=9cm，DB=2cm．请求出CF的长度．

查看试题解析
23. 在平面直角坐标系xOy中，直线l₁：y＝3x与直线l₂：y＝kx+b交于点 $A (a ， 3)$ ．

(1)、求a的值；

(2)、直接写出关于x的不等式3x＜kx+b的解集．

查看试题解析
24. 如图，在△ABC中，∠ACB=90°，D是BC延长线上一点，E是AB上的一点，且在BD的垂直平分线EG上，DE交AC于点F，求证：点E在AF的垂直平分线上．

查看试题解析
25. 某公司保安部去商店购买同一品牌的应急灯和手电筒，查看定价后发现，购买一个应急灯和5个手电筒共需50元，购买3个应急灯和2个手电筒共需85元．

(1)、求出该品牌应急灯、手电筒的定价分别是多少元？

(2)、经商谈，商店给予该公司购买一个该品牌应急灯赠送一个该品牌手电筒的优惠，如果该公司需要手电筒的个数是应急灯个数的2倍还多8个，且该公司购买应急灯和手电筒的总费用不超过670元，那么该公司最多可购买多少个该品牌应急灯？

查看试题解析
26. 【阅读学习】
课堂上，老师带领同学们学习了“提公因式法、公式法”两种因式分解的方法．分解因式的方法还有许多，如分组分解法．它的定义是：将一个多项式分组后，可提公因式或运用公式继续分解的方法叫分组分解法．使用这种方法的关键在于分组适当，而在分组时，必须有预见性．能预见到下一步能继续分解．例如：
（1） $a m + a n + b m + b n = (a m + b m) + (a n + b n) = m (a + b) + n (a + b) = (a + b) (m + n)$ ；
（2） $x^{2} - y^{2} - 2 y - 1 = x^{2} - (y^{2} + 2 y + 1) = x^{2} - (y + 1)^{2} = (x + y + 1) (x - y - 1)$ ．

【学以致用】

请仿照上面的做法，将下列各式分解因式：

(1)、 $a b - a - b + 1$ ；

(2)、 $4 - x^{2} + 4 x y - 4 y^{2}$ ．

(3)、【拓展应用】已知： $x + y = 7$ ， $x - y = 5$ ．求： $x^{2} - y^{2} - 2 y + 2 x$ 的值．

查看试题解析
27. 如图

(1)、如图1，△ABC中，∠BAC＝90°，AB＝AC，D，E在BC上，∠DAE＝45°，为了探究BD，DE，CE之间的等量关系，现将△AEC绕A顺时针旋转90°后成△AFB，连接DF，经探究，你所得到的BD，DE，CE之间的等量关系式是；(无须证明)

(2)、如图2，在△ABC中，∠BAC＝120°，AB＝AC，D，E在BC上，∠DAE＝60°，∠ADE＝45°，试仿照(1)的方法，利用图形的旋转变换，探究BD，DE，CE之间的等量关系，并证明你的结论．

查看试题解析
28.
如图，边长为4cm的等边△ABC中，点P、Q分别是边AB、BC上的动点（端点除外），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ，CP交于点M，在点P，Q运动的过程中．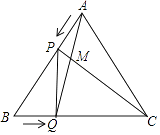

(1)、求证：△ABQ≌△CAP；

(2)、∠QMC的大小是否发生变化？若无变化，求∠QMC的度数；若有变化，请说明理由；

(3)、连接PQ，当点P，Q运动多少秒时，△PBQ是直角三角形？

查看试题解析