福建省漳州市漳浦县2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-06-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列英文大写正体字母中，既是轴对称图形，又是中心对称图形的是（）

A、S B、N C、M D、X

查看试题解析
2. 若 $a < b$ ，则运用不等式性质变形正确的是（）

A、 $a + 4 > b + 4$ B、 $a - 3 > b - 3$ C、 $\frac{1}{2} a > \frac{1}{2} b$ D、 $- 2 a > - 2 b$

查看试题解析
3. 在平面直角坐标系内，将M（6，2）先向左平移4个单位，再向下平移2个单位，则移动后的点的坐标是（）

A、（2，0） B、（10，4） C、（10，0） D、（2，4）

查看试题解析
4. 一个等边三角形的边长为2，则该三角形的高为（）

A、2 B、1 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
5. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 30 °$ ，以B为圆心，BC的长为半径画弧，交AC于点D，连接BD，则 $∠ A D B =$ （）

A、100° B、105° C、110° D、115°

查看试题解析
6. 如图，两条直线 $l_{1}$ 和 $l_{2}$ 的关系式分别为 $y_{1} = k_{1} x + b_{1}$ ， $y_{2} = k_{2} x + b_{2}$ ，两直线的交点坐标为（2，1），当 $y_{1} > y_{2}$ 时，x的取值范围为（）

A、 $x < 2$ B、 $x > 1$ C、 $x < 1$ D、 $x > 2$

查看试题解析
7. 下列命题不正确的是（）

A、一个锐角和一条边分别相等的两个直角三角形全等 B、两边分别相等的两个直角三角形全等 C、三角形经过旋转，对应线段平行且相等. D、中心对称图形上每一对对应点所连成的线段都被对称中心平分.

查看试题解析
8. 如图，在△ABC中，∠ABC＝60°，∠C＝45°，AD是BC边上的高，∠ABC的平分线BE交AD于点F，则图中共有等腰三角形（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 如果不等式组 ${\begin{array}{l} x \leq 5 \\ x > m \end{array}$ 有解，那么m的取值范围是（）

A、 $m \leq 5$ B、 $m \geq 5$ C、 $m < 5$ D、 $m > 5$

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $A C = 6$ ， $∠ A B C = 90 °$ ， BD是 $△ A B C$ 的角平分线，过点D作 $D E ⊥ B D$ 交BC边于点E.若 $A D = 2$ ，则图中阴影部分面积为（）

A、2 B、4 C、3 D、5

查看试题解析

二、填空题

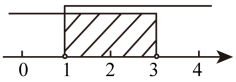
11. 如图，数轴上所表示的解集为.

查看试题解析
12. 反证法证明“钝角三角形中必有一个角小于45°”先应假设.

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $∠ A C B = 15 °$ ， $∠ A D B = 30 °$ ， $A B = 3$ ，则 $C D =$ cm.

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A E = 40 °$ ， AB的垂直平分线DE分别交AB、BC于点D、E，则 $∠ B A C =$ .

查看试题解析
15. 为有效开展“阳光体育”活动，某校计划购买篮球和排球共50个，购买资金不超过2800元.若每个篮球80元，每个排球40元，则篮球最多可购买个.

查看试题解析
16. 如图，在△ABC中，AB=AC=4，∠C=30°，P在边BC上运动，连接AP，将线段AP绕点A顺时针旋转120°至AP′，则线段PP′的最小值为.

查看试题解析

三、解答题

17. 解不等式 $4 (x - 1) > 5 x - 3$ ，并把它的解集在数轴上表示出来：

查看试题解析
18. 解不等式组 ${\begin{array}{l} \frac{x}{2} - \frac{x - 1}{3} \leq 1 \\ 5 x - 1 > 4 \end{array}$ ，并写出它的整数解.

查看试题解析
19. 如图，O为 $∠ B A C$ 内一点， $O E ⊥ A B$ 于点E、 $O F ⊥ A C$ 于点F，且 $A E = A F$ ，求证：AO平分 $∠ B A C$ .

查看试题解析
20. 由于灯管老化，现某学校要购进A、B两种节能灯管320只，A、B两种灯管的单价分别为25元和30元，现要求B种灯管的数量不少于A种灯管的3倍，那么购买A种灯管多少只时，可使所付金额最少？最少为多少元？

查看试题解析
21. 如图， $△ A B C$ 中， $∠ A = ∠ A B C$ .

(1)、作BC的垂直平分线交BC于点D，交AC于点E

(2)、连接BE，若 $B E = B A$ ，求 $∠ C$ 的度数.

查看试题解析
22. $△ A B C$ 在平面直角坐标系xOy中的位置如图所示.

⑴将 $△ A B C$ 向下平移5个单位再向左平移1个单位得到 $△ A_{1} B_{1} C_{1}$ ，作出平移后的 $△ A_{1} B_{1} C_{1}$ .

⑵将 $△ A B C$ 绕点O顺时针旋转 $90 °$ 得到 $△ A_{2} B_{2} C_{2}$ ，作出旋转后的 $△ A_{2} B_{2} C_{2}$ .

⑶ $△ A_{2} B_{2} C_{2}$ 可由 $△ A_{1} B_{1} C_{1}$ 旋转得到，旋转中心是 ▲ .

查看试题解析
23. 如图，已知 $△ A B C$ 的面积为16， $B C = 8$ .现将 $△ A B C$ 沿直线BC向右平移a个单位到 $△ D E F$ 的位置.

(1)、连接AD，四边形ABFD的面积为32时，求a的值；

(2)、连接AE、AD，当 $A B = 5$ ， $a = 5$ 时，试判断 $△ A D E$ 的形状，并说明理由.

查看试题解析
24. 阅读以下例题：解不等式： $(x + 4) (x - 1) > 0$
解：①当 $x + 4 > 0$ ，则 $x - 1 > 0$

即可以写成： ${\begin{array}{l} x + 4 > 0 \\ x - 1 > 0 \end{array}$ ，解不等式组得： ${\begin{array}{l} x > - 4 \\ x > 1 \end{array}$

②当若 $x + 4 < 0$ ，则 $x - 1 < 0$

即可以写成： ${\begin{array}{l} x + 4 < 0 \\ x - 1 < 0 \end{array}$ 解不等式组得： ${\begin{array}{l} x < - 4 \\ x < 1 \end{array}$

综合以上两种情况：不等式解集： $x > 1$ 或 $x < - 4$ .

以上解法的依据为：当 $a b > 0$ ，则 $a > 0$ ， $b > 0$ 或 $a < 0$ ， $b < 0$

(1)、若 $a b < 0$ ，则 $a > 0$ ， b0或 $a < 0$ ， b0

(2)、请你模仿例题的解法，解不等式：
① $(x + 2) (x - 3) > 0$ ；

② $(x + 1) (x - 2) < 0$ .

查看试题解析
25. 如图

【问题背景】

如图1，等腰直角△ABC中，AB＝AC，∠BAC＝90°，则边BC与边AB的数量关系为BC＝ $\sqrt{2}$ AB.

(1)、如图2，等腰△ABC中，AB＝AC，∠BAC＝120°，作AD⊥BC于点D，则得到边BC与边AB的数量关系为.

(2)、【迁移应用】
如图3，△ABC和△ADE都是等腰三角形，∠BAC＝∠DAE＝120°，D、E、C三点共线，连接BD，
①求证：△ADB≌△AEC.

②求AD、BD、CD之间的数量关系.

(3)、【拓展延伸】
如图4，△ABC与△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，AB＝6 $\sqrt{3}$ ，连接BD并延长，交AC于点F.若∠CBF＝15°，∠BAD＝30°，则四边形AEFD的面积为

查看试题解析