广西钦州市浦北县2021-2022学年七年级下学期期中考试数学试卷

试卷更新日期：2022-06-01 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列各数中，无理数的是（）

A、 $\frac{1}{7}$ B、0 C、 $\sqrt{2}$ D、3.14

查看试题解析
2. 北京2022年冬奥会会徽以汉字“冬”为灵感来源，图形上半部分展现滑冰运动员的造型，下半部分表现滑雪运动员的英姿.如图，下列选项中，可以由平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 点 $P (- 4 ， 7)$ 到y轴的距离是（）

A、－4 B、3 C、4 D、7

查看试题解析
4.
如图所示，下列说法错误的是（　　）

A、∠A和∠B是同旁内角 B、∠A和∠3是内错角 C、∠1和∠3是内错角 D、∠C和∠3是同位角

查看试题解析
5. 如图，在数轴上表示实数 $\sqrt{15}$ 的点可能（）．

A、点P B、点Q C、点M D、点N

查看试题解析
6. 下列命题是假命题的是（）

A、对顶角相等 B、两直线平行，同旁内角相等 C、同位角相等，两直线平行 D、平行于同一条直线的两直线平行

查看试题解析
7. 下列运算正确的是（）

A、 $- 2^{2} = 4$ B、 ${(\sqrt[3]{- 5})}^{3} = 5$ C、 $\sqrt{4} = \pm 2$ D、 $| - 2 | = 2$

查看试题解析
8. 如图，在下列给出的条件中，能判定AB//CD的是（）

A、∠BAD+∠BCD＝180° B、∠CDB＝∠ABD C、∠ADB＝∠DBC D、∠ABE＝∠FAD

查看试题解析
9. 如图所示，已知点O是直线CD上的一点，∠AOC＝30°，OB平分∠AOD，则∠BOD的度数是（）

A、75° B、65° C、55° D、45°

查看试题解析
10. 学校在李老师家的南偏东 $30 °$ 方向，距离是500m，则李老师家在学校的（）

A、北偏东 $30 °$ 方向，相距500m处 B、北偏西 $30 °$ 方向，相距500m处 C、北偏东 $60 °$ 方向，相距500m处 D、北偏西 $60 °$ 方向，相距500m处

查看试题解析
11. 如果m是任意实数，则点 $P (m - 4 ， m + 1)$ 一定不在

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，对于点 $P (x ， y)$ 我们把点 $P (- y + 1 ， x + 1)$ 叫做点 $P$ 的伴随点.已知点 $A_{1}$ 的伴随点为 $A_{2}$ ，点 $A_{2}$ 的伴随点为 $A_{3}$ ，点 $A_{3}$ 的伴随点为 $A_{4}$ ， …这样依次得到点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， …， $A_{n}$ ， ….若点 $A_{1}$ 的坐标为 $(2 ， 4)$ ，点 $A_{2022}$ 的坐标为（）

A、 $(- 3 ， 3)$ B、 $(- 2 ， - 2)$ C、 $(3 ， - 1)$ D、 $(2 ， 4)$

查看试题解析

二、填空题

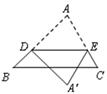
13. 计算 $\sqrt[3]{1000}$ 的值为.

查看试题解析
14. 在电影票上，如果将“8排4号”记作 $(8 ， 4)$ ，那么 $(10 ， 3)$ 确定的位置是.

查看试题解析
15. 如图，△ABC中， DE∥BC，将△ADE沿DE翻折，使得点A落在平面内的A′处，若∠B＝40°，则∠BDA′的度数是.

查看试题解析
16. 若a，b均为正整数，且a＞ $\sqrt{7}$ ， b＜ $\sqrt[3]{2}$ ，则a＋b的最小值是.

查看试题解析
17. 如图，将长为 $5 c m$ ，宽为 $3 c m$ 的长方形 $A B C D$ 先向右平移 $2 c m$ ，再向下平移 $1 c m$ ，得到长方形 $A^{'} B^{'} C^{'} D^{'}$ ，则阴影部分的面积为 $c m^{2}$ ．

查看试题解析
18. 如图，已知AB∥CD，则∠A、∠C、∠P的关系为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{5} (\sqrt{5} - 3)$ ；

(2)、 $\sqrt{2} (\sqrt{2} + \frac{1}{\sqrt{2}})$ .

查看试题解析
20. 求下列各式中 $x$ 的值：

(1)、 ${(x - 2)}^{3} = 27$ ；

(2)、 $64 x^{2} - 81 = 0$ .

查看试题解析
21. 在平面直角坐标系中，△ABC三个顶点坐标分别为：A（﹣3，﹣1），B（﹣2，﹣4），C（1，﹣3）.

(1)、在网格中建立平面直角坐标系，并作出△ABC；

(2)、画出将△ABC向上平移3个单位长度，再向右平移2个单位长度得到的△A₁B₁C₁ ，并写出B₁的坐标.

查看试题解析
22. 完成下面的证明.
如图， $E$ ， $F$ 分别在 $A B$ 和 $C D$ 上， $∠ 1 = ∠ D$ ， $∠ 2$ 与 $∠ C$ 互余， $A F ⊥ C E$ 于点 $G$ .求证 $A B ∥ C D$ .

证明：∵ $A F ⊥ C E$ （已知），

∴ $∠ C G F = 90 °$ （垂直的定义）.

∵ $∠ 1 = ∠ D$ （已知），

∴   ∥   （   ）.

∴ $∠ 4 = ∠ C G F = 90 °$ （   ）.

又∵ $∠ 2 + ∠ C = 90 °$ （已知），

$∠ 2 + ∠ 3 + ∠ 4 =$   （平角的定义），

∴ $∠ 2 + ∠ C = ∠ 2 + ∠ 3 = 90 °$ .

∴ $∠ C =$   .

∴ $A B ∥ C D$ （   ）.

查看试题解析
23. 如图，直线AB、CD相交于点O，OE平分∠BOC，∠COF=90°，

(1)、若∠BOE=70°，求∠AOF的度数；

(2)、若∠BOD：∠BOE=1：2，求∠AOF的度数．

查看试题解析
24. 已知点A（3a﹣6，a+1），试分别根据下列条件，求出点A的坐标，

(1)、点A在x轴上；

(2)、点A在过点P（3，﹣2），且与y轴平行的直线上．

查看试题解析
25. 如图1，已知直线 $P Q ∥ M N$ ，点A在直线PQ上，点B，C在直线MN上，连接AB，AC， $∠ P A B = 50 °$ ， $∠ A C B = 30 °$ ， AD平分 $∠ P A C$ ， BD平分 $∠ A B C$ ， AD与BD相交于点D.

(1)、求 $∠ A D B$ 的度数；

(2)、若将图1中的线段AC沿MN向右平移到 $A_{1} C_{1}$ ，如图2，此时 $A_{1} D$ 平分 $∠ A A_{1} C_{1}$ ， $B D$ 平分 $∠ A B C_{1}$ ， $A_{1} D$ 与BD相交于点D， $∠ P A B = 50 °$ ， $∠ A_{1} C_{1} B = 30 °$ ，求 $∠ A_{1} D B$ 的度数；

(3)、若将图1中的线段AC沿MN向左平移到 $A_{1} C_{1}$ ，如图3，其他条件与（2）相同，求此时 $∠ A_{1} D B$ 的度数.

查看试题解析