湖南省长沙市周南教育集团2021-2022学年九年级下学期期中考试数学试卷
试卷更新日期:2022-06-01 类型:期中考试
一、单选题
-
1. 9的算术平方根是( )A、 B、 C、 D、2. 六个大小相同的正方体搭成的几何体如图所示,其俯视图是( )
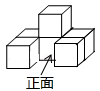 A、
A、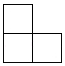 B、
B、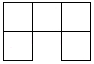 C、
C、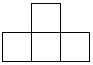 D、
D、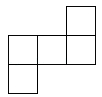 3. 下列计算正确的是( )A、 B、 C、 D、4. 不等式组 的解在数轴上表示为( )A、
3. 下列计算正确的是( )A、 B、 C、 D、4. 不等式组 的解在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、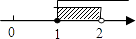 5. 下列命题正确的是( )A、矩形对角线互相垂直 B、方程 的解为 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等6. 一把直尺和一块三角板 (含 、 角)如图所示摆放,直尺一边与三角板的两直角边分别交于点 和点 ,另一边与三角板的两直角边分别交于点 和点 ,且 ,那么 的大小为( )
5. 下列命题正确的是( )A、矩形对角线互相垂直 B、方程 的解为 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等6. 一把直尺和一块三角板 (含 、 角)如图所示摆放,直尺一边与三角板的两直角边分别交于点 和点 ,另一边与三角板的两直角边分别交于点 和点 ,且 ,那么 的大小为( )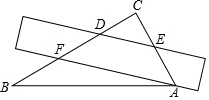 A、 B、 C、 D、7. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
A、 B、 C、 D、7. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( ) A、 B、1 C、 D、28. 《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积= (弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )
A、 B、1 C、 D、28. 《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积= (弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )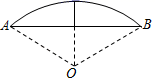 A、 B、 C、 D、9. 为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 万元购买甲型机器人和用 万元购买乙型机器人的台数相同,两型号机器人的单价和为 万元.若设甲型机器人每台 万元,根据题意,所列方程正确的是( )A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),交x轴于A,B两点,交y轴于C.则:
A、 B、 C、 D、9. 为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 万元购买甲型机器人和用 万元购买乙型机器人的台数相同,两型号机器人的单价和为 万元.若设甲型机器人每台 万元,根据题意,所列方程正确的是( )A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),交x轴于A,B两点,交y轴于C.则:①b=﹣2;
②该二次函数图象与y轴交于负半轴;
③存在这样一个a,使得M、A、C三点在同一条直线上;
④若a=1,则OA•OB=OC2 .
以上说法正确的有( )
A、①②③④ B、②③④ C、①②④ D、①②③二、填空题
-
11. 分解因式: .12. 若一组数据2,3,x,1,5,7的众数为7,则这组数据的中位数为.13. 已知圆锥的底面积为16 cm2 , 母线长为6cm,则圆锥的侧面积是cm2 .14. 如果关于 的一元二次方程 有两个不相等的实数根,那么 的取值范围是 .15. 甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是: , , 则射击成绩较稳定的是.(填“甲”或“乙”)16. 如图,在平行四边形ABCD中,E在DC上,若DE:EC=2:3,则AF:AC=.

三、解答题
-
17. 计算:.18. 先化简,再求值:
,其中 .
19. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都是格点. (1)、将△ABC绕点A逆时针旋转90°得到△A1B1C1;
(1)、将△ABC绕点A逆时针旋转90°得到△A1B1C1;
作△A1B1C1关于点O成中心对称的△A2B2C2;(2)、B1B2的长为;四边形C2B2C1B1的面积为.20. 为庆祝中国共产党建党100周年,周南集团某校组织全体学生进行了党史知识学习,并举行了党史知识竞赛,参赛学生均获奖.为了解本次竞赛获奖的分布情况,从中随机抽取了部分学生的获奖结果进行统计分析,学生的得分为整数,依据得分情况将获奖结果分为四个等级:A级为特等奖,B级(81—90分)为一等奖,C级(71—80分)为二等奖,D级(70分及以下)为三等奖,将统计结果绘制成了如图所示的两幅不完整的统计图,根据统计图中的信息解答下列问题: (1)、本次被抽取的部分学生人数是人;(2)、扇形统计图中表示B级的扇形圆心角的度数是 ▲ , 并把条形统计图补充完整;(3)、九年级一班有4名获特等奖的学生小明、小亮、小聪、小军,班主任要从中随机选择两名同学进行经验分享,利用列表法或画树状图,求小军被选中的概率.21. 如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F .
(1)、本次被抽取的部分学生人数是人;(2)、扇形统计图中表示B级的扇形圆心角的度数是 ▲ , 并把条形统计图补充完整;(3)、九年级一班有4名获特等奖的学生小明、小亮、小聪、小军,班主任要从中随机选择两名同学进行经验分享,利用列表法或画树状图,求小军被选中的概率.21. 如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F . (1)、求证:四边形ADCF是菱形;(2)、若AC=12,AB=16,求菱形ADCF的面积.22. 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)、学校准备购进这两种
(1)、求证:四边形ADCF是菱形;(2)、若AC=12,AB=16,求菱形ADCF的面积.22. 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元;(2)、学校准备购进这两种 型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由. 23. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧的中点BD交AC于点E.
型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由. 23. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧的中点BD交AC于点E. (1)、若 , 求.(2)、求证:AD2=DE•DB.(3)、若BC=5,CD= , 求DE的长.24. 新定义:如果函数G的图象与直线l相交于点A(x1 , y1)和点B(x2 , y2),那么我们把|x1−x2|叫做函数G在直线l上的“截距”.(1)、求双曲线G:与直线l:上的“截距”;(2)、若抛物线与直线相交于点A(x1 , y1)和点B(x2 , y2),若“截距”为 , 且x1<x2<0,求b的值;(3)、设m,n为正整数,且 , 抛物线在x轴上的“截距”为d1 , 抛物线在x轴上的“截距”为d2.如果对一切实数t恒成立,求m,n的值.25. 已知一次函数: 与x轴交于点A,与y交于点C. 抛物线 (a、m为常数)过定点B,连接BC,点D为线段BC上一动点.
(1)、若 , 求.(2)、求证:AD2=DE•DB.(3)、若BC=5,CD= , 求DE的长.24. 新定义:如果函数G的图象与直线l相交于点A(x1 , y1)和点B(x2 , y2),那么我们把|x1−x2|叫做函数G在直线l上的“截距”.(1)、求双曲线G:与直线l:上的“截距”;(2)、若抛物线与直线相交于点A(x1 , y1)和点B(x2 , y2),若“截距”为 , 且x1<x2<0,求b的值;(3)、设m,n为正整数,且 , 抛物线在x轴上的“截距”为d1 , 抛物线在x轴上的“截距”为d2.如果对一切实数t恒成立,求m,n的值.25. 已知一次函数: 与x轴交于点A,与y交于点C. 抛物线 (a、m为常数)过定点B,连接BC,点D为线段BC上一动点. (1)、求出点B的坐标;(2)、过D作DP⊥AC于点P,DQ⊥x于点Q,设Q点横坐标为t,DP长度为d,试求d关于t的函数解析式;(3)、①当m=0,a>0时,该抛物线上存在唯一的点H使∠CAH=45°,求此时抛物线的解析式;
(1)、求出点B的坐标;(2)、过D作DP⊥AC于点P,DQ⊥x于点Q,设Q点横坐标为t,DP长度为d,试求d关于t的函数解析式;(3)、①当m=0,a>0时,该抛物线上存在唯一的点H使∠CAH=45°,求此时抛物线的解析式;②过点D作DE⊥BC交线段OB于点E,连接CE并延长交△OBC的外接圆于点F,当点D在BC上移动时,求 的最大值.