广西南宁地区2022年初中毕业班第一次适应性测试数学试卷
试卷更新日期:2022-06-01 类型:中考模拟
一、单选题
-
1. 下列各数中,比0小的数是( )A、2 B、0 C、-1 D、32. 为推动世界冰雪运动的发展,我国将于2022年举办北京冬奥会.在此之前进行了冬奥会会标的征集活动,以下是部分参选作品,其文字上方的图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 某校将要召开夏季运动会,七年级二班的小丁决定随机从跳高、跳远和短跑中选择一个项目进行报名,若选择这三个项目的可能性都相同,则小丁恰好选择短跑参赛项目的概率是( )A、 B、 C、 D、4. 2022年2月,广西百色疫情形势严峻,牵动了大家的心.面对疫情,我们切不可掉以轻心,要做好日常防护.科学研究表明,导致新冠肺炎的新冠病毒比细菌小很多,平均直径仅为0.000000098,这个数据0.000000098用科学记数法表示为( )A、 B、 C、 D、5. 下列调查方式,你认为最合适全面调查的是( )A、检测某品牌鲜奶是否符合食品卫生标准 B、乘坐地铁前的安检 C、了解广西壮族自治区中学生视力情况 D、了解全国中学生观看冬奥会节目的情况6. 下列各式计算正确的是( )A、 B、 C、 D、7. 反比例函数y= 的图象位于( )A、第一、三象限 B、第二、三象限 C、第一、二象限 D、第二、四象限8. 如图, 的直径 垂直于弦 ,垂足是点 , , ,则 的长为( )
3. 某校将要召开夏季运动会,七年级二班的小丁决定随机从跳高、跳远和短跑中选择一个项目进行报名,若选择这三个项目的可能性都相同,则小丁恰好选择短跑参赛项目的概率是( )A、 B、 C、 D、4. 2022年2月,广西百色疫情形势严峻,牵动了大家的心.面对疫情,我们切不可掉以轻心,要做好日常防护.科学研究表明,导致新冠肺炎的新冠病毒比细菌小很多,平均直径仅为0.000000098,这个数据0.000000098用科学记数法表示为( )A、 B、 C、 D、5. 下列调查方式,你认为最合适全面调查的是( )A、检测某品牌鲜奶是否符合食品卫生标准 B、乘坐地铁前的安检 C、了解广西壮族自治区中学生视力情况 D、了解全国中学生观看冬奥会节目的情况6. 下列各式计算正确的是( )A、 B、 C、 D、7. 反比例函数y= 的图象位于( )A、第一、三象限 B、第二、三象限 C、第一、二象限 D、第二、四象限8. 如图, 的直径 垂直于弦 ,垂足是点 , , ,则 的长为( ) A、 B、 C、6 D、129. 如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A、 B、 C、6 D、129. 如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( ) A、 n mile B、60 n mile C、120 n mile D、 n mile10. 我国古代数学名著《张邱建算经》中记载:“今有清洒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )A、 B、 C、 D、11. 如图,抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,下列结论中正确的有( )
A、 n mile B、60 n mile C、120 n mile D、 n mile10. 我国古代数学名著《张邱建算经》中记载:“今有清洒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )A、 B、 C、 D、11. 如图,抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,下列结论中正确的有( )① ,②方程 的两个根是 , ,③ ,④当 时,x的取值范围是 .
 A、①② B、①②③ C、①③④ D、②④12. 如图,在 中, , .点F是 边上一点.将 沿直线 翻折得到 , 交 与点E.连接 ,若 ,则 ( )
A、①② B、①②③ C、①③④ D、②④12. 如图,在 中, , .点F是 边上一点.将 沿直线 翻折得到 , 交 与点E.连接 ,若 ,则 ( )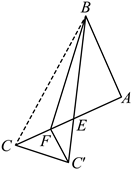 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
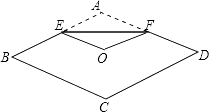
13. 若二次根式 有意义,则x的取值范围是 .14. 分解因式:.15. 已知单项式 与 是同类项,则m+n= .16. 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=cm.
 17. 如图,在扇形AOB中, ,半径OC交弦AB于点D,且 ,若 ,则阴影部分的面积为.
17. 如图,在扇形AOB中, ,半径OC交弦AB于点D,且 ,若 ,则阴影部分的面积为. 18. 如图,四边形 是边长为3的正方形, 的平分线 交 于点E,点M、点N分别是 和 上的动点,连接 ,则当 的值最小时, .
18. 如图,四边形 是边长为3的正方形, 的平分线 交 于点E,点M、点N分别是 和 上的动点,连接 ,则当 的值最小时, .
三、解答题
-
19. 计算: .20. 解不等式组 ,并写出这个不等式组的整数解.21. 如图,在 中,D是 边上一点,且 .
 (1)、尺规作图(保留作图痕迹,不写作法)
(1)、尺规作图(保留作图痕迹,不写作法)①作 的角平分线交 于点E;
②作线段 的垂直平分线交 于点F.
(2)、连接 ,直接写出线段 和 的数量关系及位置关系.22. 每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:八年级抽取的学生的竞赛成绩:
4,10,8,6,6,6,7,7,7,6,9,9,8,8,8,8,8,9,10,4.
七年级抽取的学生的竞赛成绩条形统计图

七、八年级抽取的学生的竞赛成绩统计表
年级
七年级
八年级
平均数
7.4
7.4
中位数
a
b
众数
7
c
合格率
85%
90%
根据以上信息,解答下列问题:
(1)、填空:a= , b= , c=;(2)、估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数;(3)、根据以上数据分析,你认为该校哪个年级“国家安全法”知识竞赛的学生成绩更优异?请说明理由.23.
【阅读理解】倍长中线是初中数学一种重要的数学思想,如图①,在 中, 是 边上的中线,若延长 至E,使 ,连接 ,可根据 证明 ,则 .(1)、【类比探究】如图②,在 中, , ,点G是 的中点,求中线 的取值范围;(2)、【拓展应用】如图③,在四边形 中, ,点E是 的中点.若 是 的平分线.试探究 , , 之间的等量关系,并证明你的结论.24. 众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到A地和B地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:
A地(元/辆)
B地(元/辆)
大货车
900
1000
小货车
500
700
现安排上述装好物资的20辆货车(每辆大货车装15吨物资,每辆小货车装10吨物资)中的10辆前往A地,其余前往B地,设前往A地的大货车有x辆,这20辆货车的总运费为y元.
(1)、这20辆货车中,大货车、小货车各有多少辆?(2)、求 与 的函数解析式,并直接写出 的取值范围;(3)、若运往A地的物资不少于140吨,求总运费y的最小值.25. 如图,将矩形 置放在平面直角坐标系中,顶点O与坐标原点重合,点A和点C的坐标分别为 , .抛物线 经过点A和B,且 . (1)、求抛物线的解析式;(2)、如果点P由点B开始沿边 以每秒1个单位长度的速度向终点A运动,同时点Q由点C开始沿边 以每秒2个单位长度的速度向终点B运动,设运动时间为t秒. 的面积为S.
(1)、求抛物线的解析式;(2)、如果点P由点B开始沿边 以每秒1个单位长度的速度向终点A运动,同时点Q由点C开始沿边 以每秒2个单位长度的速度向终点B运动,设运动时间为t秒. 的面积为S.①写出S与t之间的函数关系式,并写出t的取值范围;
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?若存在,请求出R点的坐标;若不存在,请说明理由.
26. 如图,在 中,直径 与弦 互相垂直,垂足为H,点E是弧 上一点,连接 ,过点E作直线 交 的延长线于点M,交 的延长线于点G,连接 交 于点F,且 . (1)、求证: 是 的切线;(2)、若 ,求证: ;(3)、在(2)的条件下,若 , ,求 的值.
(1)、求证: 是 的切线;(2)、若 ,求证: ;(3)、在(2)的条件下,若 , ,求 的值.