广西柳州市柳南区2022年九年级教学实验研究质量抽测数学试卷(二模)
试卷更新日期:2022-06-01 类型:中考模拟
一、单选题
-
1. 计算的结果等于( )A、-5 B、-1 C、1 D、52. 下列图形中,可能是圆锥侧面展开图的是( )
 A、
A、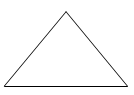 B、
B、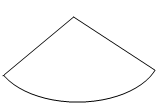 C、
C、 D、
D、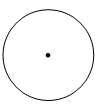 3. 近年来,5G在全球发展迅猛,中国成为这一领域基础设施建设、技术与应用落地的一大推动者.截至2021年3月底,中国已建成819000座5G基站,占全球70%以上.数据819000用科学记数法表示为( )A、 B、 C、 D、4. 如图,已知四条线段 , , , 中的一条与挡板另一侧的线段 在同一直线上,请借助直尺判断该线段是( )
3. 近年来,5G在全球发展迅猛,中国成为这一领域基础设施建设、技术与应用落地的一大推动者.截至2021年3月底,中国已建成819000座5G基站,占全球70%以上.数据819000用科学记数法表示为( )A、 B、 C、 D、4. 如图,已知四条线段 , , , 中的一条与挡板另一侧的线段 在同一直线上,请借助直尺判断该线段是( ) A、 B、 C、 D、5. 在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理:这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A、 B、 C、 D、5. 在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理:这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )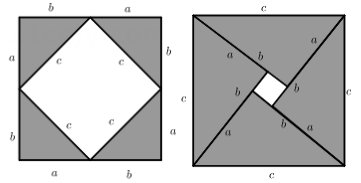 A、统计思想 B、分类思想 C、数形结合思想 D、函数思想6. 若分式 的值等于0,则x的值是( )A、2 B、﹣2 C、3 D、﹣37. 将一副直角三角板按如图方式摆放,若直线 , 则的大小为( )
A、统计思想 B、分类思想 C、数形结合思想 D、函数思想6. 若分式 的值等于0,则x的值是( )A、2 B、﹣2 C、3 D、﹣37. 将一副直角三角板按如图方式摆放,若直线 , 则的大小为( )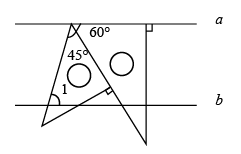 A、 B、 C、 D、8. 已知不等式组 ,其解集在数轴上表示正确的是( )A、
A、 B、 C、 D、8. 已知不等式组 ,其解集在数轴上表示正确的是( )A、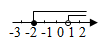 B、
B、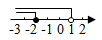 C、
C、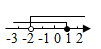 D、
D、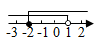 9. 在中考体育加试中,某班30名男生的跳远成绩如下表:
9. 在中考体育加试中,某班30名男生的跳远成绩如下表:成绩/m
1.95
2.00
2.05
2.10
2.15
2.25
人数
2
3
9
8
5
3
这些男生跳远成绩的众数、中位数分别是( )
A、2.10,2.05 B、2.10,2.10 C、2.05,2.10 D、2.05,2.0510. 如图,点在上, , 则( )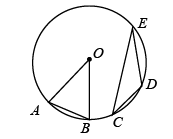 A、48° B、24° C、22° D、21°11. 如图,已知线段 ,利用尺规作 的垂直平分线,步骤如下:①分别以点 为圆心,以 的长为半径作弧,两弧相交于点 和 .②作直线 .直线 就是线段 的垂直平分线.则 的长可能是( )
A、48° B、24° C、22° D、21°11. 如图,已知线段 ,利用尺规作 的垂直平分线,步骤如下:①分别以点 为圆心,以 的长为半径作弧,两弧相交于点 和 .②作直线 .直线 就是线段 的垂直平分线.则 的长可能是( ) A、1 B、2 C、3 D、412. 某口罩厂有26名工人,每人每天可以生产800个口罩面或1000个口罩耳绳.一个口罩面需要配两个耳绳,为使每天生产的口罩刚好配套,设安排x名工人生产口罩面,根据题意可列方程为( )A、 B、 C、 D、
A、1 B、2 C、3 D、412. 某口罩厂有26名工人,每人每天可以生产800个口罩面或1000个口罩耳绳.一个口罩面需要配两个耳绳,为使每天生产的口罩刚好配套,设安排x名工人生产口罩面,根据题意可列方程为( )A、 B、 C、 D、二、填空题
-
13. 计算:.14. 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在岔路口随机选择一条路径,它获得食物的概率是 。
 15. 方程的解是.16. 若点、在同一个反比例函数的图象上,则的值为.17. 添项、拆项是因式分解中常用的方法,比如分解多项式可以用如下方法分解因式:
15. 方程的解是.16. 若点、在同一个反比例函数的图象上,则的值为.17. 添项、拆项是因式分解中常用的方法,比如分解多项式可以用如下方法分解因式:①;
又比如多项式可以这样分解:
②;
仿照以上方法,分解多项式的结果是.
18. 如图,在正方形ABCD中,点O是对角线BD的中点,点P在线段OD上,连接AP并延长交CD于点E,过点P作交BC于点F,连接AF、EF,AF交BD于G,以下三个结论:①;②;③为定值.其中正确的结论有.(填入正确的序号即可).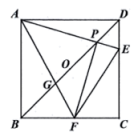
三、解答题
-
19. 计算:20. 解二元一次方程组: .21. 如图,点 在一条直线上, .
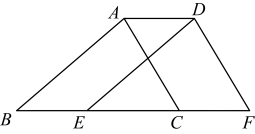 (1)、求证: ;(2)、连接 ,求证:四边形 是平行四边形.22. 如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据: ≈1.732)
(1)、求证: ;(2)、连接 ,求证:四边形 是平行四边形.22. 如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据: ≈1.732) 23. “勤劳”是中华民族的传统美德,同学们在家里除了“停课不停学”还帮助父母做一些力所能及的家务,在本学期开学初,小马同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间划分为五个类别: , , , , .并将调查结果制成如图两幅不完整的统计图,根据统计图提供的信息,解答下列问题:
23. “勤劳”是中华民族的传统美德,同学们在家里除了“停课不停学”还帮助父母做一些力所能及的家务,在本学期开学初,小马同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间划分为五个类别: , , , , .并将调查结果制成如图两幅不完整的统计图,根据统计图提供的信息,解答下列问题: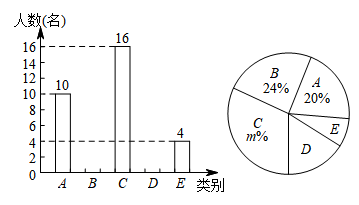 (1)、本次共调查了名学生;扇形统计图中m的值是;(2)、直接在答题卡中补全条形统计图;(3)、若该校有1200名学生,根据抽样调查的结果,请你估计该校有多少学生寒假在家做家务的总时间不低于20小时.24. 如图,在平面直角坐标系中,直线AB与反比例函数的图象交于点和点 , 与x轴交于点C,与y轴交于点D.
(1)、本次共调查了名学生;扇形统计图中m的值是;(2)、直接在答题卡中补全条形统计图;(3)、若该校有1200名学生,根据抽样调查的结果,请你估计该校有多少学生寒假在家做家务的总时间不低于20小时.24. 如图,在平面直角坐标系中,直线AB与反比例函数的图象交于点和点 , 与x轴交于点C,与y轴交于点D.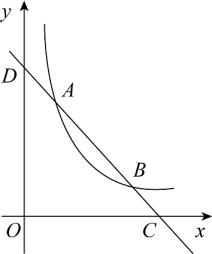 (1)、求反比例函数的表达式及一次函数解析式;(2)、双曲线上是否存在一点P,使点P到原点的距离最小,如果存在,求出P点坐标,并求出最小距离.如果不存在,请说明理由.25. 如图,已知AB是⊙O的弦,点C是弧AB中点,D是弦AB上一动点,且不与A、B重合,CD的延长线交⊙O于E,连接AE、BE,过点A作 , 垂足F,.
(1)、求反比例函数的表达式及一次函数解析式;(2)、双曲线上是否存在一点P,使点P到原点的距离最小,如果存在,求出P点坐标,并求出最小距离.如果不存在,请说明理由.25. 如图,已知AB是⊙O的弦,点C是弧AB中点,D是弦AB上一动点,且不与A、B重合,CD的延长线交⊙O于E,连接AE、BE,过点A作 , 垂足F,.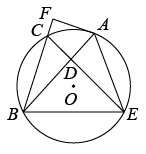 (1)、求证:AF是⊙O的切线;(2)、若 , , 则DE的长是多少?(3)、当点D在弦AB上运动时,的值是否发生变化?如果变化,写出其变化范围;如果不变,求出其值.26. 如图,已知抛物线与x轴交于 , 两点,与y轴交于点.
(1)、求证:AF是⊙O的切线;(2)、若 , , 则DE的长是多少?(3)、当点D在弦AB上运动时,的值是否发生变化?如果变化,写出其变化范围;如果不变,求出其值.26. 如图,已知抛物线与x轴交于 , 两点,与y轴交于点. (1)、求该抛物线的表达式;(2)、点P是抛物线在第一象限上的点,连接AC,CP,AP,若沿着直线AP翻折后点C的对应点E恰好落在x轴上,求P点的坐标;(3)、在抛物线对称轴上是否存在点M,使得是锐角?若存在,求出点M的纵坐标m的取值范围;若不存在,请说明理由.
(1)、求该抛物线的表达式;(2)、点P是抛物线在第一象限上的点,连接AC,CP,AP,若沿着直线AP翻折后点C的对应点E恰好落在x轴上,求P点的坐标;(3)、在抛物线对称轴上是否存在点M,使得是锐角?若存在,求出点M的纵坐标m的取值范围;若不存在,请说明理由.