广西柳州市柳城县2022年初中毕业升学模拟考试数学试卷（一）

试卷更新日期：2022-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. -8的立方根是（）

A、4 B、±2 C、2 D、-2

查看试题解析
2.
如图，与∠1是同位角的是（　　）

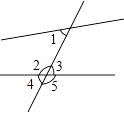A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
3. 计算（﹣a²b）³的结果是（）

A、﹣a⁶b³ B、a⁶b C、3a⁶b³ D、﹣3a⁶b³

查看试题解析
4. 七年级1班甲、乙两个小组的14名同学身高（单位：厘米）如下：
甲组
158
159
160
160
160
161
169
乙组
158
159
160
161
161
163
165
以下叙述错误的是（）

A、甲组同学身高的众数是160 B、乙组同学身高的中位数是161 C、甲组同学身高的平均数是161 D、两组相比，乙组同学身高的方差大

查看试题解析
5. 下列交通标志中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在平面直角坐标系中，点A坐标为 $(3 ， 4)$ ，那么 $\cos α$ 的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. 如图，在 $△ A B C$ 中，D，E分别是AB和AC上的点，且 $D E ∥ B C$ ，若 $A E = 1$ ， $C E = A D = 2$ ，则AB的长是（）

A、6 B、5 C、4 D、2

查看试题解析
8. 若分式 $\frac{x^{2} - 9}{2 x - 6}$ 的值为零，则x的值为（）.

A、3 B、3或-3 C、0 D、-3

查看试题解析
9. 对于函数y＝﹣2x+1，下列结论正确的是（）

A、它的图象必经过点（﹣1，3） B、它的图象经过第一、二、三象限 C、当 $x > \frac{1}{2}$ 时，y＞0 D、y值随x值的增大而增大

查看试题解析
10. 如图，已知⊙O是△ABC的内切圆，且∠ABC＝60°，∠ACB＝80°，则∠BOC的度数为（）

A、110° B、120° C、130° D、140°

查看试题解析
11. 用配方法解方程x²＋6x－4＝0，下列配方正确的是（）

A、 $(x + 3)^{2} = 4$ B、 $(x + 3)^{2} = 5$ C、 $(x - 3)^{2} = 13$ D、 $(x + 3)^{2} = 13$

查看试题解析
12. 如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC＝60°，顶点C的纵坐标为 $6 \sqrt{3}$ ，反比例函数 $y = \frac{k}{x}$ 的图象与菱形对角线AO交于点D，连接BD，当BD⊥x轴时，k的值是（）

A、12 $\sqrt{3}$ B、-12 $\sqrt{3}$ C、-48 $\sqrt{3}$ D、-48

查看试题解析

二、填空题

13. 如图，点D是线段AB的中点，C是线段AD的中点，若AB＝8cm，则CD＝cm.

查看试题解析
14. 方程2x－3＝1的解是.

查看试题解析
15. 如图，Rt△ABC中，∠C＝90°，AB的垂直平分线DE交AC于点E，连接BE.若∠A＝40°，则∠CBE的度数为.

查看试题解析
16. 某种品的标价为120元，若以九折降价出售，仍获利20%，该商品的进货价为元．

查看试题解析
17. 甲、乙两人骑自行车匀速同向行驶，乙在甲前面100米处，同时出发去距离甲1300米的目的地，其中甲的速度比乙的速度快.设甲、乙之间的距离为 $y$ 米，乙行驶的时间为 $x$ 秒， $y$ 与 $x$ 之间的关系如图所示，则甲的速度为每秒米.

查看试题解析
18. 已知：如图，在Rt△ABC中，BC＝AC＝2，点M是AC边上一动点，连接BM，以CM为直径的⊙O交BM于N，则线段AN的最小值为.

查看试题解析

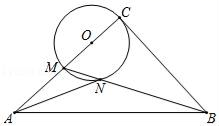
三、解答题

19. 计算：﹣2²＋（π﹣3.14）⁰﹣3tan30°＋ $\sqrt{27}$

查看试题解析
20. 求一元一次不等式组 ${\begin{array}{l} - 3 (x - 2) \geq 4 - x \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$ 的解集.

查看试题解析
21. 为推进“传统文化进校园”活动，某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图（每人只能选择一个小组）：

(1)、报名参加课外活动小组的学生共有 ▲ 人，将条形图补充完整；

(2)、扇形图中m= ， n=；

(3)、根据报名情况，学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组，甲、乙恰好都被安排到“地方戏曲”小组的概率是多少？请用列表或画树状图的方法说明.

查看试题解析
22. 为应对新型冠状病毒，某药店老板到厂家选购A、B两种品牌的医用外科口罩，B品牌口罩每个进价比A品牌口罩每个进价多0.7元，若用7200元购进A品牌的数量是用5000元购进B品牌数量的2倍．

(1)、求A、B两种品牌的口罩每个进价分别为多少元？

(2)、若A品牌口罩每个售价为2.1元，B品牌口罩每个售价为3元，药店老板决定一次性购进A、B两种品牌口罩共8000个，在这批口罩全部出售后所获利润不低于3000元．则最少购进B品牌口罩多少个？

查看试题解析
23. 在平面直角坐标系xOy中，一次函数 $y = - x + 5$ 的图象与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象相交于A，B两点，与x轴相交于点C，连接OB，且 $△ B O C$ 的面积为 $\frac{5}{2}$ .

(1)、求反比例函数的表达式；

(2)、将直线AB向下平移，若平移后的直线与反比例函数的图象只有一个交点，试说明直线AB向下平移了几个单位长度？

查看试题解析
24. 在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F.

(1)、求证：四边形ADCF是菱形；

(2)、若AC＝4，AB＝5，求菱形ADCF的面积.

查看试题解析
25. 如图1，⊙O是△ABC的外接圆，AB为⊙O的直径，在△ABC外侧作∠CAD＝∠CAB，过点C作CD⊥AD于点D，交AB延长线于点P.

(1)、求证：PC是⊙O的切线；

(2)、连接OD交AC于点G，若OG：GD＝2：3，求∠P的度数；

(3)、如图2，作弦CF平分∠ACB，交AB于点E，连接BF，若BF＝5 $\sqrt{2}$ ， tan∠PCB＝ $\frac{1}{2}$ ，求线段PB的长.

查看试题解析
26. 如图，抛物线 $y = - \frac{1}{2} x^{2} + b x + 2$ 交x轴于A（ $- 1$ ， 0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点.

(1)、求抛物线解析式；

(2)、过点P作y轴的垂线与射线BC交于点Q，设线段PQ的长度为d，点P的横坐标为m，求d与m的函数关系式；

(3)、若点P在y轴右侧，过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′.是否存在点P，使Q′恰好落在x轴上？若存在，求出点P的坐标；若不存在，说明理由.

查看试题解析

甲组	158	159	160	160	160	161	169
乙组	158	159	160	161	161	163	165