广西贺州市八步区2022年初中学业水平模拟考试数学试卷(一)
试卷更新日期:2022-06-01 类型:中考模拟
一、单选题
-
1. 在实数1,2,0,-1中,最大的数为( )A、1 B、2 C、0 D、-12. 如图,两直线a,b被直线c所截,已知a∥b,∠1=62°,则∠2的度数为( )
 A、128° B、98° C、108° D、118°3. 下列图案中既是中心对称图形,又是轴对称图形的是( )A、
A、128° B、98° C、108° D、118°3. 下列图案中既是中心对称图形,又是轴对称图形的是( )A、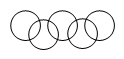 B、
B、 C、
C、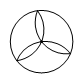 D、
D、 4. 2021年5月15日7时18分,执行我国首次火星探测任务的“天问一号”探测器在火星着落,在火星上首次留下中国印迹.火星是太阳系九大行星之一,火星的半径约为3395000米,用科学记数法表示“3395000”为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 一组数据7,8,3,8,4的中位数是( )A、3 B、6 C、7 D、87. 多项式2ax2 4ax 2a因式分解为( )A、a(2x-1)2 B、a(2x+1)2 C、2a(x+1)2 D、2a(x-1)28. 关于x的一元二次方程x2﹣4x+3=0的解为( )A、x1=﹣1,x2=3 B、x1=1,x2=﹣3 C、x1=1,x2=3 D、x1=﹣1,x2=﹣39. 已知圆锥的底面直径为4,母线长为6,则此圆锥侧面展开图的圆心角是( )A、240° B、150° C、120° D、90°10. 如图,一次函数 和反比例函数 的图象交于 , 两点,若当 时,则x的取值范围是( )
4. 2021年5月15日7时18分,执行我国首次火星探测任务的“天问一号”探测器在火星着落,在火星上首次留下中国印迹.火星是太阳系九大行星之一,火星的半径约为3395000米,用科学记数法表示“3395000”为( )A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 一组数据7,8,3,8,4的中位数是( )A、3 B、6 C、7 D、87. 多项式2ax2 4ax 2a因式分解为( )A、a(2x-1)2 B、a(2x+1)2 C、2a(x+1)2 D、2a(x-1)28. 关于x的一元二次方程x2﹣4x+3=0的解为( )A、x1=﹣1,x2=3 B、x1=1,x2=﹣3 C、x1=1,x2=3 D、x1=﹣1,x2=﹣39. 已知圆锥的底面直径为4,母线长为6,则此圆锥侧面展开图的圆心角是( )A、240° B、150° C、120° D、90°10. 如图,一次函数 和反比例函数 的图象交于 , 两点,若当 时,则x的取值范围是( ) A、 或 B、 或 C、 或 D、 或11. 如图,AB是⊙O的直径,点C、D位于直径AB的两侧.若∠ABC=40°,则∠BDC的度数是( )
A、 或 B、 或 C、 或 D、 或11. 如图,AB是⊙O的直径,点C、D位于直径AB的两侧.若∠ABC=40°,则∠BDC的度数是( ) A、50° B、40° C、60° D、45°12. 我们规定:若 , 则.如 , , 则 , 已知 , 则的最小值为( )A、1 B、2 C、3 D、4
A、50° B、40° C、60° D、45°12. 我们规定:若 , 则.如 , , 则 , 已知 , 则的最小值为( )A、1 B、2 C、3 D、4二、填空题
-
13. 若 有意义,则 的取值范围是14. 全国第七次人口普查已经结束,请问在这次人口普查中采用的调查方式是.15. 已知P1(﹣1,y1),P2(﹣2,y2)在函数y=2x+b的图象上,则y1y2.(填写>,<或者=)16. 如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,BD=1,DE=4,则BC等于.
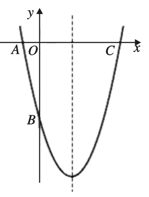
 17. 二次函数=的部分图象如图,图象过点 , 对称轴为直线=2,下列结论:①bc<0;②=;③;④(为任意实数);⑤当时,的值随值的增大而增大;其中正确的结论有(填序号).
17. 二次函数=的部分图象如图,图象过点 , 对称轴为直线=2,下列结论:①bc<0;②=;③;④(为任意实数);⑤当时,的值随值的增大而增大;其中正确的结论有(填序号). 18. 如图,在正方形ABCD中, ,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G , 连接BG . 若 ,则BG的最小值为 .
18. 如图,在正方形ABCD中, ,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G , 连接BG . 若 ,则BG的最小值为 .
三、解答题
-
19. 计算:.20. 解分式方程: .21. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.22. 如图,在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是45°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度.(参考数据:≈1.73,≈1.41,结果保留整数).
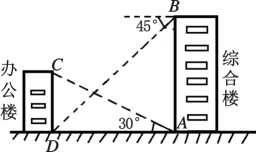 23. 如图,矩形ABCD的对角线AC与BD相交于点O,CEBD,DEAC,AD= , DE=2.
23. 如图,矩形ABCD的对角线AC与BD相交于点O,CEBD,DEAC,AD= , DE=2.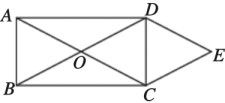 (1)、求证:四边形OCED是菱形;(2)、求四边形OCED的面积.24. 第24届冬季奥林匹克运动会将于2022年2月4日至2022年2月20日在北京市和张家口市联合举行,北京是唯一一个既举办冬季奥运会又举办夏季奥运会的城市.为了迎接2022年北京冬季奥运会,某校准备举行冬季长跑比赛,为奖励长跑优胜者,学校需要购买一些冬奥会吉祥物冰墩墩、雪容融中性笔和徽章.了解到某商店中性笔的单价比徽章的单价多11元,若买2支中性笔和3个徽章共需67元.(1)、中性笔和徽章的单价各是多少元?(2)、该商店推出两种优惠方案,方案一:消费金额超过200元的部分打八折;方案二:全店商品打九折.若学校需要购买10支中性笔和30个徽章,选择哪种方案更优惠?
(1)、求证:四边形OCED是菱形;(2)、求四边形OCED的面积.24. 第24届冬季奥林匹克运动会将于2022年2月4日至2022年2月20日在北京市和张家口市联合举行,北京是唯一一个既举办冬季奥运会又举办夏季奥运会的城市.为了迎接2022年北京冬季奥运会,某校准备举行冬季长跑比赛,为奖励长跑优胜者,学校需要购买一些冬奥会吉祥物冰墩墩、雪容融中性笔和徽章.了解到某商店中性笔的单价比徽章的单价多11元,若买2支中性笔和3个徽章共需67元.(1)、中性笔和徽章的单价各是多少元?(2)、该商店推出两种优惠方案,方案一:消费金额超过200元的部分打八折;方案二:全店商品打九折.若学校需要购买10支中性笔和30个徽章,选择哪种方案更优惠?