广西贺州市2022年初中学业水平模拟考试数学试卷（二模）

试卷更新日期：2022-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数是无理数的是（）

A、0 B、1 C、2 D、 $π$

查看试题解析
2. 如图，直线 $a ∥ b$ ， $∠ 1 = 66 °$ ，则 $∠ 2$ 等于（）

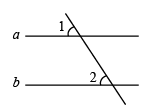A、66° B、33° C、24° D、14°

查看试题解析
3. 小贺同学统计宿舍里几位同学的体重分别是（单位：千克）：46，48，45，52，44，50，43，48，这组数据的中位数是（）

A、45 B、46 C、47 D、48

查看试题解析
4. 下面四个几何体中，主视图为三角形的是（）

A、 B、 C、 D、

查看试题解析
5. 我市今年中考报名人数约33700人，将数据33700用科学记数法表示是（）

A、 $33.7 \times 1 0^{3}$ B、 $3.37 \times 1 0^{4}$ C、 $0.337 \times 1 0^{5}$ D、 $3.37 \times 1 0^{5}$

查看试题解析
6. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 $a^{2} + a^{2} = a^{4}$ C、 $a^{2} \cdot a^{3} = a^{5}$ D、 $(2 x)^{2} = 2 x^{2}$

查看试题解析
7. 二元一次方程组 ${\begin{array}{l} 3 x + y + 1 = 0 \\ 3 y = 2 x + 19 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 2 \\ y = - 5 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 5 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = - 5 \end{array}$ D、 ${\begin{array}{l} x = - 2 \\ y = 5 \end{array}$

查看试题解析
8. 若 $4 a^{2} b^{n - 1}$ 与 $a^{m} b^{2}$ 是同类项，则 $m + n$ 的值是（）

A、6 B、5 C、4 D、3

查看试题解析
9. 如图，在边长为4的等边△ABC中，D是BC边上的中点，以点A为圆心，AD为半径作圆与AB，AC分别交于E，F两点，求 $\overset{⌢}{E F}$ 的长为（）

A、 $\frac{2 \sqrt{3}}{3} π$ B、 $\frac{\sqrt{3}}{3} π$ C、 $\frac{3 \sqrt{3}}{2} π$ D、 $3 \sqrt{3} π$

查看试题解析
10. 一次函数y＝ax＋a(a为常数，a≠0)与反比例函数y＝ $\frac{a}{x}$ (a为常数，a≠0)在同一平面直角坐标系内的图象大致为（）

A、 B、 C、 D、

查看试题解析
11. 已知二次函数 $y = - x^{2} + 2 x + 1$ ，当 $a \leq x \leq 0$ 时，y取得最小值为 $- 2$ ，则a的值为（）

A、-1 B、0 C、1 D、2

查看试题解析
12. 一装有某种液体的圆柱形容器，半径为6cm，高为18cm.小强不小心碰倒，容器水平静置时其截面如图所示，其中圆心O到液面AB的距离为3cm，若把该容器扶正竖直，则容器中液体的高度为（）

A、 $\frac{4 π - 3 \sqrt{3}}{12 π} c m$ B、 $\frac{12 π - 9 \sqrt{3}}{2 π} c m$ C、 $\frac{12 π - 9 \sqrt{3}}{π} c m$ D、 $\frac{12 π - 9 \sqrt{3}}{2} c m$

查看试题解析

二、填空题

13. 要使分式 $\frac{1}{x + 2}$ 有意义，则x的取值范围为．

查看试题解析
14. 分解因式： $a^{2} + 2 a b + b^{2} - 4 =$ .

查看试题解析
15. 从1，2，4三个数字中随机抽取两个组成一个两位数，这个两位数能整除3的概率为.

查看试题解析
16. 如图，在平面直角坐标系中，点A的坐标为 $(0 ， a)$ ，点B的坐标为 $(b ， 0)$ ，连接AB.若将 $△ A B O$ 绕点B顺时针旋转90°，得到 $△ A^{^{'}} B^{^{'}} O^{^{'}}$ ，则点 $A^{'}$ 的坐标为（用含a，b的代数式表示）.

查看试题解析
17. 已知二次函数y=x²−6x+7与x轴交于A(x₁ ， 0)，B(x₂ ， 0)两点，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}} =$ .

查看试题解析
18. 如图，半圆O以AB为直径，四边形ABCD是半圆O的内接四边形，延长BC，AD交于点E，DC=BC=4，AD=14，求AB的长.

查看试题解析

三、解答题

19. 计算： ${(\sqrt{3})}^{2} + (2 - π)^{0} - | - 3 | + \sqrt{2} c o s 45 °$ .

查看试题解析
20. 解分式方程： $\frac{1}{x + 3} = \frac{x}{x - 3} - 1$ .

查看试题解析
21. 某中学开展主题为“科学防控，健康你我”疫情防控知识竞赛，要求每班选派三人参赛，某班现有5个学生报名参加，其中2男3女，计划在这5个学生中随机抽选两个参加该校疫情防控知识竞赛，请用列表或画树状图的方法求所选两个学生中恰好是一个男生和一个女生的概率.

查看试题解析
22. 如图，点C为某市图书馆，一辆拖拉机沿公路从点A开始向正东方向行驶，点A位于点C南偏西60°，拖拉机以 $18 k m / h$ 的速度行驶100m到达点B，此时点B位于点C南偏西30°，拖拉机行驶到点B时，图书馆刚好受到拖拉机噪音影响，如果拖拉机继续沿正东方面行驶，图书馆受噪音影响的时间为多少分钟？

查看试题解析
23. 如图，在矩形ABCD中，O为BD的中点，过点O作 $E F ⊥ B D$ 分别交BC，DA于点E，F.

(1)、求证：四边形BEDF是菱形；

(2)、若AB＝3， $B C = 6$ ，求 $△ A B F$ 的面积.

查看试题解析
24. 脱贫攻坚的收官之年，老李在驻村干部的帮助下，利用网络平台进行“直播带货”，销售一批成本为每件30元的商品，按单价不低于成本价，且不高于60元销售，经调查发现，该商品每天的销售量y（件）与销售单价x（元）之间满足一次函数关系，部分数据如表所示.
销售单价x（元）
30
40
45
销售数量y（件）
100
80
70

(1)、求该商品每天的销售量y（件）与销售单价x（元）之间的函数关系式.

(2)、销售单价定为多少元时，才能使销售该商品每天获得的利润w（元）最大？最大利润是多少元？

查看试题解析
25. 如图，以 $△ A B C$ 的边AB为直径作 $⊙ O$ ，与BC交于点D，E是 $\overset{⌢}{B D}$ 的中点，连接AE交BC于点F， $∠ A C B = 2 ∠ B A E$ .

(1)、求证：AC是 $⊙ O$ 的切线；

(2)、若 $C D = 3$ ， $t a n ∠ A C B = 2$ ，求BC的长.

查看试题解析
26. 如图，抛物线经过点 $A (- 1 ， 0)$ ， $C (0 ， 3)$ 两点，对称轴为 $x = \frac{5}{2}$ .

(1)、求抛物线的表达式；

(2)、若过点C的直线l的表达式为 $y = k x + 3$ ，当直线l与抛物线有两个不同交点时，求k的取值范围；

(3)、在（2）条件下，当直线l与BC垂直时，与对称轴交于点E.此时抛物线上是否存在点P，使得 $S_{△ A B P} = S_{△ A B E}$ ，若存在，求点P的坐标；若不存在，请说明理由.

查看试题解析

销售单价x（元）	30	40	45
销售数量y（件）	100	80	70