广西河池市凤山县2022年中考数学适应性诊断试卷
试卷更新日期:2022-06-01 类型:中考模拟
一、单选题
-
1.
实数a,b,c,d在数轴上的对应点的位置如图所示,其中互为相反数的两个数是( )
 A、a和d B、a和c C、b和d D、b和c2. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
A、a和d B、a和c C、b和d D、b和c2. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )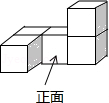 A、
A、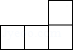 B、
B、 C、
C、 D、
D、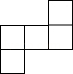 3. 近几年,沙尘暴肆虐我国北方,这与土地沙漠化有直接关系,据测算,我国因土地沙漠化造成的经济损失平均每天为1.5亿元人民币,若一年按365天计算,用科学记数法表示我国一年因土地沙漠化造成的经济损失为( )A、元 B、元 C、元 D、元4. 下列运算正确的是( )A、 B、 C、 D、5. 下列调查方式合适的是( )A、为了了解电视机的使用寿命,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、调查某中学七年级一班学生视力情况,采用抽样调查的方式 D、为了了解巢湖水资源质量,采用抽样调查的方式6. 下列方程是关于的一元二次方程的是( )A、 B、 C、 D、7. 同时抛掷两枚质地均匀的正六面体骰子,向上两个数字之积为偶数的概率是( )A、 B、 C、 D、8. 已知等腰三角形的两边长分别为5cm和7cm,则这个等腰三角形的周长是( )A、7cm B、16cm C、19cm D、17cm或19cm9. 如图,与位似,位似中心为点 , , 的周长为 , 则周长为( )
3. 近几年,沙尘暴肆虐我国北方,这与土地沙漠化有直接关系,据测算,我国因土地沙漠化造成的经济损失平均每天为1.5亿元人民币,若一年按365天计算,用科学记数法表示我国一年因土地沙漠化造成的经济损失为( )A、元 B、元 C、元 D、元4. 下列运算正确的是( )A、 B、 C、 D、5. 下列调查方式合适的是( )A、为了了解电视机的使用寿命,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、调查某中学七年级一班学生视力情况,采用抽样调查的方式 D、为了了解巢湖水资源质量,采用抽样调查的方式6. 下列方程是关于的一元二次方程的是( )A、 B、 C、 D、7. 同时抛掷两枚质地均匀的正六面体骰子,向上两个数字之积为偶数的概率是( )A、 B、 C、 D、8. 已知等腰三角形的两边长分别为5cm和7cm,则这个等腰三角形的周长是( )A、7cm B、16cm C、19cm D、17cm或19cm9. 如图,与位似,位似中心为点 , , 的周长为 , 则周长为( ) A、 B、6 C、4 D、10. 已知甲做100个零件所需要的时间和乙做90个零件所用的时间相同,又知每小时甲、乙两人共做35个机器零件.求甲、乙每小时分别做的零件数,则( )A、若设甲每小时做个零件,则: B、若设甲每小时做个零件,则: C、若设乙每小时做个零件,则: D、若设乙每小时做个零件,则:11. 如图,点A(a,1),B(b,3)都在双曲线上,点P,Q分别是x轴,y轴上的动点,则四边形ABQP周长的最小值为( )
A、 B、6 C、4 D、10. 已知甲做100个零件所需要的时间和乙做90个零件所用的时间相同,又知每小时甲、乙两人共做35个机器零件.求甲、乙每小时分别做的零件数,则( )A、若设甲每小时做个零件,则: B、若设甲每小时做个零件,则: C、若设乙每小时做个零件,则: D、若设乙每小时做个零件,则:11. 如图,点A(a,1),B(b,3)都在双曲线上,点P,Q分别是x轴,y轴上的动点,则四边形ABQP周长的最小值为( ) A、 B、 C、 D、12. 若点在轴上,则点在第( )象限.A、一 B、二 C、三 D、四
A、 B、 C、 D、12. 若点在轴上,则点在第( )象限.A、一 B、二 C、三 D、四二、填空题
-
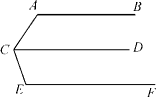
13. 如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=度.
 14. 分解因式: .15. 当 时,分式有意义;当 时,分式的值为零.16. 如图,△ABC是边长为6的等边三角形,点D在BC的延长线上,作DF⊥AB,垂足为F,若CD=4,则AF的长等于.
14. 分解因式: .15. 当 时,分式有意义;当 时,分式的值为零.16. 如图,△ABC是边长为6的等边三角形,点D在BC的延长线上,作DF⊥AB,垂足为F,若CD=4,则AF的长等于. 17. 在菱形中, , , 则菱形的边长等于 , 面积等于.18. 如图反比例函数图象过 , 则的面积为.
17. 在菱形中, , , 则菱形的边长等于 , 面积等于.18. 如图反比例函数图象过 , 则的面积为.
三、解答题
-
19. 计算:20. 先化简,再求值: , 其中 , .21. 已知直线及其两侧两点、 , 如图.

⑴在直线上求作一点 , 使;(写出简单的作图过程)
⑵在直线上求作一点 , 使平分.(写出简单的作图过程)
22. 为了促进各科均衡发展,学校准备在九年级下期开设四科补短班,分别是英语、数学、物理和化学.为提前了解同学们最想参加的科目,学校在开学前采用随机抽样方式进行了调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息完成以下问题. (1)、扇形统计图中,“英语”所在扇形的圆心角度数是 , 并补全条形统计图;(2)、在被调查的学生中,选择化学的有2名女同学,其余为男同学,现要从中随机抽取2名同学参加学科座谈会,请用画树状图或列表的方法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.23. 图是安装在房间墙壁上的壁挂式空调,图是安装该空调的侧面示意图,空调风叶是绕点由上往下旋转扫风的,安装时要求:当风叶恰好吹到床的外边沿,此时风叶与竖直线的夹角为 , 空调底部垂直于墙面 , 米,米,床铺长米,求安装的空调底部位置距离床的高度是多少米?(结果精确到米)
(1)、扇形统计图中,“英语”所在扇形的圆心角度数是 , 并补全条形统计图;(2)、在被调查的学生中,选择化学的有2名女同学,其余为男同学,现要从中随机抽取2名同学参加学科座谈会,请用画树状图或列表的方法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.23. 图是安装在房间墙壁上的壁挂式空调,图是安装该空调的侧面示意图,空调风叶是绕点由上往下旋转扫风的,安装时要求:当风叶恰好吹到床的外边沿,此时风叶与竖直线的夹角为 , 空调底部垂直于墙面 , 米,米,床铺长米,求安装的空调底部位置距离床的高度是多少米?(结果精确到米) 24. 某单位需要购买一些钢笔和笔记本.若购买2支钢笔和1本笔记本需42元,购买3支钢笔和2本笔记本需68元.(1)、求买一支钢笔要多少钱?(2)、若购买了钢笔和笔记本共50件,付款可能是810元吗?说明理由.25. 如图,内接于 , 过作的垂线,垂足为 , 交于 ,
24. 某单位需要购买一些钢笔和笔记本.若购买2支钢笔和1本笔记本需42元,购买3支钢笔和2本笔记本需68元.(1)、求买一支钢笔要多少钱?(2)、若购买了钢笔和笔记本共50件,付款可能是810元吗?说明理由.25. 如图,内接于 , 过作的垂线,垂足为 , 交于 , (1)、求证:弧弧;(2)、连交于 , 过作的平行线交于 , 求证:;(3)、在(2)条件下,连交于 , 若 , ∶∶ , , 求的长.26. 如图1所示,已知抛物线的顶点为 , 与轴交于、两点左右 , 与轴交于点,为抛物线上一点,且、关于抛物线的对称轴对称,作直线.
(1)、求证:弧弧;(2)、连交于 , 过作的平行线交于 , 求证:;(3)、在(2)条件下,连交于 , 若 , ∶∶ , , 求的长.26. 如图1所示,已知抛物线的顶点为 , 与轴交于、两点左右 , 与轴交于点,为抛物线上一点,且、关于抛物线的对称轴对称,作直线.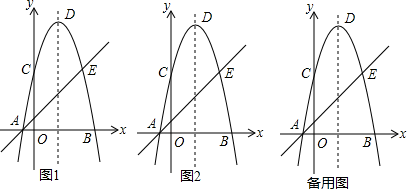 (1)、求直线的解析式;(2)、在图2中,若将直线沿轴翻折后交抛物线于点 , 则点的坐标为(直接填空);(3)、点为抛物线上一动点,过点作直线与轴平行,交直线于点 , 设点的横坐标为 , 当∶∶时,直接写出所有符合条件的值,不必说明理由.
(1)、求直线的解析式;(2)、在图2中,若将直线沿轴翻折后交抛物线于点 , 则点的坐标为(直接填空);(3)、点为抛物线上一动点,过点作直线与轴平行,交直线于点 , 设点的横坐标为 , 当∶∶时,直接写出所有符合条件的值,不必说明理由.