广西桂林市2022年中考适应性训练数学试卷
试卷更新日期:2022-06-01 类型:中考模拟
一、单选题
-
1. -2022是2022的( )A、倒数 B、相反数 C、绝对值 D、平方根2. 如图所示的几何体的俯视图是( )
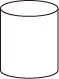 A、
A、 B、
B、 C、
C、 D、
D、 3. 已知一个数用科学记数法表示为2.1×106 , 则这个数是( )A、21000 B、210000 C、2100000 D、210000004. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、
3. 已知一个数用科学记数法表示为2.1×106 , 则这个数是( )A、21000 B、210000 C、2100000 D、210000004. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、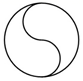 B、
B、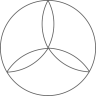 C、
C、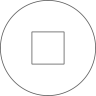 D、
D、 5. 下列各数中,是无理数的是( )A、2 B、 C、3.14159 D、6. 下列各式运算正确的是( )A、 B、 C、 D、7. 从-1,1,2,3四个数中任选2个数相乘,结果是正数的概率是( )A、 B、 C、 D、8. 如图,在菱形ABCD中,对角线AC、BD交于点O,已知AO=2,OB= , 则菱形ABCD的面积是( )
5. 下列各数中,是无理数的是( )A、2 B、 C、3.14159 D、6. 下列各式运算正确的是( )A、 B、 C、 D、7. 从-1,1,2,3四个数中任选2个数相乘,结果是正数的概率是( )A、 B、 C、 D、8. 如图,在菱形ABCD中,对角线AC、BD交于点O,已知AO=2,OB= , 则菱形ABCD的面积是( )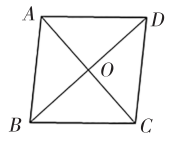 A、 B、 C、4 D、99. 已知m是一元二次方程的一个根,则的值是( )A、4 B、6 C、8 D、1010. 如图,在中,AC=BC=6, , 则边AB的长是( )
A、 B、 C、4 D、99. 已知m是一元二次方程的一个根,则的值是( )A、4 B、6 C、8 D、1010. 如图,在中,AC=BC=6, , 则边AB的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 8的立方根为.12. 若二次根式 有意义,则x的取值范围是 .13. 一组数据3,5,6,6,5的平均数是.14. 如图,在平行四边形ABCD中,AB:AD=2:3,BC=6,则平行四边形ABCD的周长是.
 15. 如图,在中, , , AE是的角平分线,点D是AB上的一点,且AD=AC,连接DE,则.
15. 如图,在中, , , AE是的角平分线,点D是AB上的一点,且AD=AC,连接DE,则.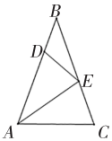 16. 如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+3k与x轴,y轴,反比例函数的图象分别交于点A,点B,点C,若AC=3BC,则k的值为.
16. 如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+3k与x轴,y轴,反比例函数的图象分别交于点A,点B,点C,若AC=3BC,则k的值为.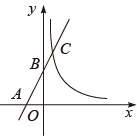
三、解答题
-
17. 计算:2+(-2)×3.18. 计算:.19. 解不等式组:.20. 如图,在平面直角坐标系中,已知ABC的三个顶点的坐标分别是A(2,3),B(1,1),C(3,1).

⑴画出ABC关于x轴对称的A1B1C1;
⑵若点P是ABC与A1B1C1的对称中心,请直接写出点P的坐标;
⑶以点O为位似中心,在y轴的左侧将ABC放大到原来的2倍,得到A2B2C2 , 请画出A2B2C2.
21. 如图,已知点B,E,C,F在同一条直线上,AC与DE交于点M, , , .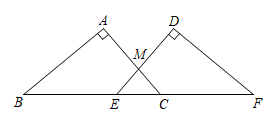 (1)、证明:;(2)、若 , 求的度数.22. 2022年北京冬奥会共设7个大项,15个分项和109个小项的比赛项目,北京冬奥会和残奥会的成功举办,点亮了“共创未来”的人类进步之光.某校体育组为了解全校学生对7个大项中“最喜欢观看的冬奥会比赛项目:A(滑雪),B(滑冰),C(冰球),D(冰壶),E(其他)”的情况(只选一项),随机抽取了部分学生进行调查,根据调查结果绘制出如下不完整的统计图.
(1)、证明:;(2)、若 , 求的度数.22. 2022年北京冬奥会共设7个大项,15个分项和109个小项的比赛项目,北京冬奥会和残奥会的成功举办,点亮了“共创未来”的人类进步之光.某校体育组为了解全校学生对7个大项中“最喜欢观看的冬奥会比赛项目:A(滑雪),B(滑冰),C(冰球),D(冰壶),E(其他)”的情况(只选一项),随机抽取了部分学生进行调查,根据调查结果绘制出如下不完整的统计图.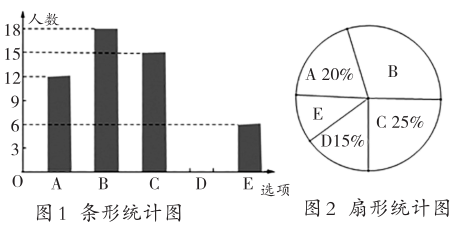
请你根据统计图回答下列问题:
(1)、请列式求本次调查共抽取多少名学生?(2)、请补全条形统计图(图1);(3)、在扇形统计图中,“B(滑冰)”所对应的圆心角是多少度?(4)、请你估计全校1200名学生中,最喜欢观看“E(其他)”项目的有多少人?23. 为了进一步丰富市民的休闲生活,某区政府决定在漓江沿岸扩建5400米绿道并进行招标,根据招标结果,该工程由甲、乙两个工程队参与建设.已知:甲工程队每天完成的工程量是乙队的1.2倍,甲队单独完成工程比乙队单独完成少用10天.(1)、求乙队每天能完成多少米?(2)、若甲、乙两个工程队合作20天后,剩余工程由乙工程队单独完成,求乙工程队还需多少天?24. 如图,已知AB是⊙O的直径,BC与⊙O相切于点B,⊙O的弦ADCO,连接DB交CO于点F,延长CO与⊙O交于点E,连接EB. (1)、求证:CD是⊙O的切线.(2)、求证:2BF2=AD⋅CF.(3)、若 , OC=5,求tan∠ABE的值.25. 如图,抛物线经过点和点 , 与x轴交于点C和点D,点A为线段CD的中点,直线y=kx-1过点A,与y轴交于点B.
(1)、求证:CD是⊙O的切线.(2)、求证:2BF2=AD⋅CF.(3)、若 , OC=5,求tan∠ABE的值.25. 如图,抛物线经过点和点 , 与x轴交于点C和点D,点A为线段CD的中点,直线y=kx-1过点A,与y轴交于点B.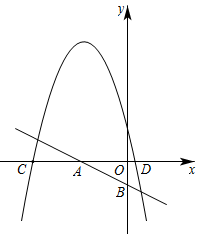 (1)、求抛物线的函数表达式.(2)、在第三象限内,以AB为边作正方形ABMN,请求出点M和点N的坐标.(3)、在(2)的条件下,点P是x轴上方抛物线上的一点,以AB为一边,以点P为对角线的交点作平行四边形ABEF,当平行四边形ABEF的面积恰好是正方形ABMN的面积的4倍时,求出点P的横坐标.
(1)、求抛物线的函数表达式.(2)、在第三象限内,以AB为边作正方形ABMN,请求出点M和点N的坐标.(3)、在(2)的条件下,点P是x轴上方抛物线上的一点,以AB为一边,以点P为对角线的交点作平行四边形ABEF,当平行四边形ABEF的面积恰好是正方形ABMN的面积的4倍时,求出点P的横坐标.