备考浙教版中考数学题型专项训练 方程与不等式选择题专练
试卷更新日期:2022-05-31 类型:三轮冲刺
一、单选题
-
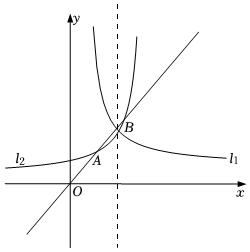
1. 如图,反比例函数图象的表达式为(),图象与图象关于直线对称,直线与交于 , 两点,当为中点时,则的值为( )
 A、 B、 C、 D、2. 对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
A、 B、 C、 D、2. 对于一元二次方程ax2+bx+c=0(a≠0),下列说法:①若a+b+c=0,则b2-4ac≥0;②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;④若x0是一元二次方程ax2+bx+c=0的根,则b2-4ac=(2ax0+b)2.
其中正确的是( )
A、①②④ B、①②③ C、①③④ D、②③④3. 已知x,y为实数,且满足 ,记 的最大值为M,最小值为m,则 ( ).A、 B、 C、 D、4. 一元二次方程 ,其中 ,给出以下四个结论:(1)若方程 有两个不相等的实数根,则方程 也有两个不相等的实数根;(2)若方程 的两根符号相同,则方程 的两根符号也相同;(3)若 是方程 的一个根,则 是方程 的一个根;(4)若方程 和方程 有一个相同的根,则这个根必是 .其中正确的个数是( )A、1 B、2 C、3 D、45. 如图,AB=30,C为射线AB上一点,BC比AC的4倍少20,P、Q两点分别从AB两点同时出发分别以2单位/秒和l单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②运动过程中,QM的长度保持不变;③AB=4NQ;④当BQ=PB时,t=12.其中正确结论的个数是( )
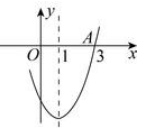
 A、1 B、2 C、3 D、46. 已知抛物线 的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示,下列结论中:
A、1 B、2 C、3 D、46. 已知抛物线 的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示,下列结论中:① ;② ;③抛物线与 轴的另一个交点的坐标为 ;④方程 有两个不相等的实数根.其中正确的个数为( )
 A、1个 B、2个 C、3个 D、4个7. 一段跑道长100米,两端分别记为点A、B.甲、乙两人分别从A、B两端同时出发,在这段跑道上来回练习跑步,甲跑步的速度是6m/s,乙跑步的速度为4m/s,练习了足够长时间,他们经过了多次相遇,相遇点离A端不可能是( )A、60米 B、0米 C、20米 D、100米8. 爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下
A、1个 B、2个 C、3个 D、4个7. 一段跑道长100米,两端分别记为点A、B.甲、乙两人分别从A、B两端同时出发,在这段跑道上来回练习跑步,甲跑步的速度是6m/s,乙跑步的速度为4m/s,练习了足够长时间,他们经过了多次相遇,相遇点离A端不可能是( )A、60米 B、0米 C、20米 D、100米8. 爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下时刻
9:00
9:45
12:00
碑上的数
是一个两位数,数字之和是9
十位与个位数字与9:00时所看到的正好相反
比9:00时看到的两位数中间多了个0
9:00时看到的两位数是( )
A、54 B、45 C、36 D、279. 如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒).若点P在运动过程中,当PB=2时,则运动时间t的值为( ) A、 秒或 秒 B、 秒或 秒或 秒或 秒 C、3秒或7秒或 秒或 秒 D、 秒或 秒或 秒或 秒10. 如图,在长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,则当△APE的面积为5cm2时,x的值为( )
A、 秒或 秒 B、 秒或 秒或 秒或 秒 C、3秒或7秒或 秒或 秒 D、 秒或 秒或 秒或 秒10. 如图,在长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,则当△APE的面积为5cm2时,x的值为( ) A、5 B、3或5 C、 D、或511. 如图,A、O、B两点在数轴上对应的数分别为﹣20、0、40,C点在A、B之间,在A、B两点处各放一个挡板,M、N两个小球同时从C处出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变.设两个小球运动的时间为t秒钟(0<t<40),当M小球第一次碰到A挡板时,N小球刚好第一次碰到B挡板.则:①C点在数轴上对应的数为0;②当10<t<25时,N在数轴上对应的数可以表示为80﹣4t;③当25<t<40时,2MA+NB始终为定值160;④只存在唯一的t值,使3MO=NO,以上结论正确的有( )
A、5 B、3或5 C、 D、或511. 如图,A、O、B两点在数轴上对应的数分别为﹣20、0、40,C点在A、B之间,在A、B两点处各放一个挡板,M、N两个小球同时从C处出发,M以2个单位/秒的速度向数轴负方向运动,N以4个单位/秒的速度向数轴正方向运动,碰到挡板后则反方向运动,速度大小不变.设两个小球运动的时间为t秒钟(0<t<40),当M小球第一次碰到A挡板时,N小球刚好第一次碰到B挡板.则:①C点在数轴上对应的数为0;②当10<t<25时,N在数轴上对应的数可以表示为80﹣4t;③当25<t<40时,2MA+NB始终为定值160;④只存在唯一的t值,使3MO=NO,以上结论正确的有( )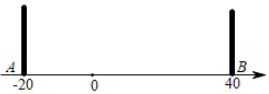 A、①②③④ B、①③ C、②③ D、①②④12. 方程|x+1|+|x-3|=4的整数解有( )A、2个 B、3个 C、5个 D、无穷多个13. 如图,已知四边形ABCD是矩形,点E在BA的延长线上, , EC分别交AD,BD于点F,G,若 , 则的值为( ).
A、①②③④ B、①③ C、②③ D、①②④12. 方程|x+1|+|x-3|=4的整数解有( )A、2个 B、3个 C、5个 D、无穷多个13. 如图,已知四边形ABCD是矩形,点E在BA的延长线上, , EC分别交AD,BD于点F,G,若 , 则的值为( ).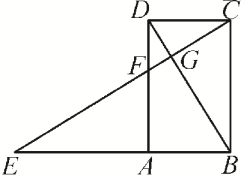 A、 B、 C、2 D、14. 某超市在“元旦”活动期间,推出如下购物优惠方案:
A、 B、 C、2 D、14. 某超市在“元旦”活动期间,推出如下购物优惠方案:①一次性购物在元(不含元)以内,不享受优惠;
②一次性购物在元(含元)以上,元(不含元)以内,一律享受九折优惠;
③一次性购物在元(含元)以上,一律享受八折优惠;
小敏在该超市两次购物分别付了90 元和270元,如果小敏把这两次购物改为一次性购物,则小敏至少需付款( )元
A、 B、 C、 D、15. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )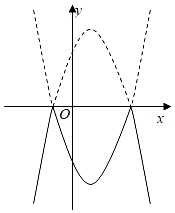 A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣316. 不等式 的整数解是1,2,3,4.则实数a的取值范围是( )A、 B、 C、 D、17. 规定: , ,例如 , ,下列结论中,
A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣316. 不等式 的整数解是1,2,3,4.则实数a的取值范围是( )A、 B、 C、 D、17. 规定: , ,例如 , ,下列结论中,
(1)能使 成立的x的值为3或-7;(2)若x<-2,则 ;(3)若 ,则2x-3y=-16;(4)式子 的最小值是4.正确的是( )A、(1)(2)(3) B、(1)(2)(4) C、(1)(3)(4) D、(1)(2)(3)(4)18. 已知抛物线y=﹣x2+bx+c与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),对称轴为l:x=1,直线y=kx+2(k≠0)与抛物线相交于两点M(x1 , y1),N(x2 , y2)(x1<x2),则|x1﹣x2|最小值为( )A、4 B、4 C、2 D、219. 若不论 取什么实数,关于 的方程 ( 、 常数)的解总是 ,则 的值是( )A、 B、 C、 D、20. 如图,现有3×3的方格,每个小方格内均有数字,要求方格内每一行.每一列以及每一条对角线上的三个数字之和均相等,记三个数字之和为P,则P的值是( )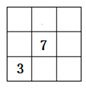 A、12 B、15 C、18 D、2121. 已知关于x,y的方程组 的解为 ,则关于方程组 的解为( )A、 B、 C、 D、22. 如图,直线k∥l, .其中 , ,则 的最大整数值是( )
A、12 B、15 C、18 D、2121. 已知关于x,y的方程组 的解为 ,则关于方程组 的解为( )A、 B、 C、 D、22. 如图,直线k∥l, .其中 , ,则 的最大整数值是( ) A、108° B、110° C、114° D、115°23. 某车间每天能生产甲种零件120个或者乙种零件100个.3个甲种零件与2个乙种零件配成一套,要在27天内生产最多的成套产品,问甲、乙两种零件各生产几天?设甲种零件生产 天,乙种零件生产 天,下列方程组正确的是( )A、 B、 C、 D、24. 已知关于 的不等式组 有且只有两个整数解,则 的取值范围是( )A、 B、 C、 D、25. 将两块完全相同的长方体木块先按图1的方式放置,再按图2的方式放置,测得的数据如图所示.则桌子的高度 ( )
A、108° B、110° C、114° D、115°23. 某车间每天能生产甲种零件120个或者乙种零件100个.3个甲种零件与2个乙种零件配成一套,要在27天内生产最多的成套产品,问甲、乙两种零件各生产几天?设甲种零件生产 天,乙种零件生产 天,下列方程组正确的是( )A、 B、 C、 D、24. 已知关于 的不等式组 有且只有两个整数解,则 的取值范围是( )A、 B、 C、 D、25. 将两块完全相同的长方体木块先按图1的方式放置,再按图2的方式放置,测得的数据如图所示.则桌子的高度 ( ) A、70 B、55 C、40 D、3026. 已知某程序如图所示,规定:从“输入实数x”到“结果是否大于95”为一次操作,如果该程序进行了两次操作停止,那么实数x的取值范围是
A、70 B、55 C、40 D、3026. 已知某程序如图所示,规定:从“输入实数x”到“结果是否大于95”为一次操作,如果该程序进行了两次操作停止,那么实数x的取值范围是 A、 B、 C、 D、27. 某超市为了回馈顾客,若一次性购物不超过300元不优惠,超过300元时按全额9折优惠.一位顾客第一次购物付款180元,第二次购物付款288元,若这两次购物付款合并一次性付款可节省( )A、18元 B、16元 C、18或46.8元 D、46.8元28. 若整数a使关于x的不等式组 无解,且使关于x的分式方程 有整数解,那么所有满足条件的a的值的积是( )A、2 B、3 C、 D、8
A、 B、 C、 D、27. 某超市为了回馈顾客,若一次性购物不超过300元不优惠,超过300元时按全额9折优惠.一位顾客第一次购物付款180元,第二次购物付款288元,若这两次购物付款合并一次性付款可节省( )A、18元 B、16元 C、18或46.8元 D、46.8元28. 若整数a使关于x的不等式组 无解,且使关于x的分式方程 有整数解,那么所有满足条件的a的值的积是( )A、2 B、3 C、 D、8