备考浙教版中考数学题型专项训练 方程与不等式解答题专练
试卷更新日期:2022-05-31 类型:三轮冲刺
一、综合题
-
1. 为了做好学校疫情防控工作,某校从药店购进一批甲、乙两种型号的口罩,已知乙种型号的口罩每袋单价比甲种型号的口罩每袋单价少5元,购买2500元的甲种口罩的数量和购买2000元的乙种口罩的数量相同.(1)、求甲、乙两种口罩每袋的售价;(2)、根据学校防疫需要,学校拟从该药店购进甲、乙两种型号口罩共800袋,其中乙种型号的数量不超过甲种型号的3倍.问学校应如何购买,才能使得购买口罩所需费用最少?并求出所需的最少费用.2. 某社区为了创建干净整洁、和谐文明的社区环境,准备购买A,B两种分类垃圾桶,通过市场调研得知:A种垃圾桶每组的单价是B种垃圾桶每组单价的1.5倍,用7200元购买A种垃圾桶的组数比用6000元购买B种垃圾桶少5组.(1)、求A,B两种垃圾桶每组单价分别是多少元;(2)、该社区计划用不超过12000元的资金购买A,B两种垃圾桶共40组,则最多可以购买A种垃圾桶多少组?3. 有一些相同的房间需要粉刷墙面,一名二级技工粉刷6个房间,5天正好完成;一名一级技工3天粉刷了4个房间还多刷了另外的 墙面.每名一级技工比二级技工一天多粉刷 墙面.(1)、求每个房间需要粉刷的墙面面积;(2)、若甲乙两名技工各自需粉刷7个房间的墙面,甲比乙每天少粉刷 ,乙比甲少用2天完成任务,求甲、乙两名技工每天各粉刷墙面面积.4. 某超市计划购进甲、乙两种水果进行销售.经了解,甲种水果和乙种水果的进价与售价如下表所示:
水果单价
甲
乙
进价(元/千克)
售价(元/千克)
20
25
已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.
(1)、求甲、乙两种水果的进价;(2)、若该超市购进这两种水果共100千克,其中甲种水果的重量不低于乙种水果重量的3倍,若全部卖完所购进的这两种水果,则超市应如何进货才能获得最大利润,最大利润是多少?5. 2022年3月12日是第44个植树节,某街道办现计划采购樟树苗和柳树苗共600棵,已知一棵柳树苗比一棵樟树苗贵4元,用2400元所购买的樟树苗与用3200所购买的柳树苗数量相同.(1)、请问一棵樟树苗的价格是多少元?(2)、若购买樟树苗的数量不超过柳树苗的2倍,怎样采购所花费用最少?最少多少元?6. 如图1,在平面直角坐标系中,大正方形OABC的边长为m厘米,小正方形ODEF的边长为n厘米,且. (1)、求点、点的坐标.(2)、起始状态如图1所示,将大正方形固定不动,小正方形以1厘米/秒的速度沿x轴向右平移,如图2.设平移的时间为t秒,在平移过程中两个正方形重叠部分的面积为S平方厘米.
(1)、求点、点的坐标.(2)、起始状态如图1所示,将大正方形固定不动,小正方形以1厘米/秒的速度沿x轴向右平移,如图2.设平移的时间为t秒,在平移过程中两个正方形重叠部分的面积为S平方厘米.①当t=1.5时,S= ▲ 平方厘米;
②在这段时间内,小正方形的一条对角线扫过的图形的面积为 ▲ 平方厘米;
③在小正方形平移过程中,若S=2,则小正方形平移的时间t为 ▲ 秒.
(3)、将大正方形固定不动,小正方形从图1中起始状态沿x轴向右平移,在平移过程中,连接AD,过D点作DM⊥AD交直线BC于M,∠DAx的角平分线所在直线和∠CMD的角平分线所在直线交于N(不考虑N点与A点重合的情形),求∠ANM的大小并说明理由.7. 已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b. (1)、求抛物线顶点Q的坐标(用含a的代数式表示);(2)、说明直线与抛物线有两个交点;(3)、直线与抛物线的另一个交点记为N.
(1)、求抛物线顶点Q的坐标(用含a的代数式表示);(2)、说明直线与抛物线有两个交点;(3)、直线与抛物线的另一个交点记为N.(Ⅰ)若-1≤a≤ , 求线段MN长度的取值范围;
(Ⅱ)求△QMN面积的最小值.
8. 今年疫情期间某物流公司计划用两种车型运输救灾物资,已知:用2辆A型车和1辆B型车装满物资一次可运10吨;用1辆A型车和2辆B型车一次可运11吨.某物流公司现有31吨货物资,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满.(1)、1辆A型车和1辆B型车都装满物资一次可分别运多少吨?(2)、请你帮该物流公司设计租车方案;(3)、若A型车每辆需租金每次100元,B型车租金每次120元,请选出最省钱的租车方案,并求出最少租车费.9. 如图,在长方形 中,边 、 的长 是方程 的两个根.点 从点 出发,以每秒 个单位的速度沿 边 的方向运动,运动时间为 秒 . (1)、求 与 的长;(2)、当点 运动到边 上时,试求出使 长为 时运动时间 的值;(3)、当点 运动到边 上时,是否存在点 ,使 是等腰三角形?若存在,请求出运动时间 的值;若不存在,请说明理由.10. 在一次地震中,某村受地震影响严重,已经成为一片废墟.为重建家园,政府准备修建在地震中受损的一条公路,若由甲工程队单独修需3个月完成,每月耗资12万元;若由乙工程队单独修建需6个月完成,每月耗资5万元.(1)、请问若由甲、乙两工程队合作修建需几个月完成?共耗资多少万元?(2)、若由甲、乙两工程队先合作,剩下的由乙队来完成,且恰好历时4个月完成修建任务,求这样安排共耗资多少万元?(时间按整月计算)11. 某产家在甲、乙工厂生产同一商品,并将其分几天运往A地240吨,B地260吨,表1是两个工厂的商品记录,表2为该商品的运费标准(m,n为常数).
(1)、求 与 的长;(2)、当点 运动到边 上时,试求出使 长为 时运动时间 的值;(3)、当点 运动到边 上时,是否存在点 ,使 是等腰三角形?若存在,请求出运动时间 的值;若不存在,请说明理由.10. 在一次地震中,某村受地震影响严重,已经成为一片废墟.为重建家园,政府准备修建在地震中受损的一条公路,若由甲工程队单独修需3个月完成,每月耗资12万元;若由乙工程队单独修建需6个月完成,每月耗资5万元.(1)、请问若由甲、乙两工程队合作修建需几个月完成?共耗资多少万元?(2)、若由甲、乙两工程队先合作,剩下的由乙队来完成,且恰好历时4个月完成修建任务,求这样安排共耗资多少万元?(时间按整月计算)11. 某产家在甲、乙工厂生产同一商品,并将其分几天运往A地240吨,B地260吨,表1是两个工厂的商品记录,表2为该商品的运费标准(m,n为常数).表1
时间
甲工厂商品记录
乙工厂商品记录
甲、乙两工厂总运费
第1天
生产商品200吨
生产商品300吨
第2天
运往A地30吨
运往A地10吨,运往B地20吨
1230元
第3天
运往B地20吨
运往B地40吨
1460元
甲乙两厂往A,B地运输该商品的运费标准(单位:元/吨)
表2
目的地
工厂
A
B
甲
20
25
乙
m
n
(1)、求m,n的值.(2)、若运费标准不变,要使剩余商品按要求运往A,B两地,且总运费最少,请给出剩余商品的运输方案.(3)、若从第4天开始,运输公司将甲工厂往B地的运费提高a元/吨,乙工厂往B地的运费降低a元/吨,其中a为正整数,若可用不超过7150元的费用按要求完成剩余商品的运输,求a的最小值.12. 学校趣味运动会组织跳绳项目,购买跳绳经费最多95元.某商店有A,B,C三个型号的跳绳,跳绳价格如下表所示,已知B型长度是A型两倍,C型长度是A型三倍(同个型号跳绳长度一样),用80米绳子制作A型的数量比120米绳子制作B型的数量还多5根.规格
A型
B型
C型
单价(元/条)
4
6
9
(1)、求三种型号跳绳的长度.(2)、若购买三种跳绳经费刚好用完,其中A型和B型跳绳条数一样多,且所有跳绳总长度为120米,求购买A型跳绳的数量.(3)、若购买的跳绳长度总长度不少于100米,则A型跳绳最多买几条?13. 某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,按每吨1元收费;每月超过12吨时,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.(1)、求每吨水的市场调节价是多少元;(2)、设每月用水量为x(x>12)吨,应交水费为y元,写出y与x之间的关系式;(3)、小张家3月份用水28吨,他家应交水费多少元?14. 在平面直角坐标系中,O是坐标原点,矩形ABCO的顶点A、C分别在x轴、y轴上,已知B点坐标为 , 且a,b满足 , 若点M沿线段CB从C向B以每秒2cm的速度运动至B,同时动点N沿线段AO从A向O以同样的速度运动,当其中一个点停止时,另一个也停止运动,设运动时间为t秒,连接OM、BN; (1)、如图1,当t为何值时,四边形OMBN是菱形?(2)、如图2,将矩形OABC沿着AP折叠,点O的对应点恰好落在BC边上,连接 , 求直线的函数解析式;(3)、如图3,点P是对角线OB上一动点,点Q是OA上一动点,求的最小值.15. 阅读下列解方程组的方法,然后解答问题:
(1)、如图1,当t为何值时,四边形OMBN是菱形?(2)、如图2,将矩形OABC沿着AP折叠,点O的对应点恰好落在BC边上,连接 , 求直线的函数解析式;(3)、如图3,点P是对角线OB上一动点,点Q是OA上一动点,求的最小值.15. 阅读下列解方程组的方法,然后解答问题:解方程组时,小明发现如果用常规的代入消元法、加减消元法来解,计算量大,且易出现运算错误,他采用下面的解法则比较简单:
②-①得: , 即.③
得:.④
①-④得: , 代入③得.
所以这个方程组的解是.
(1)、请你运用小明的方法解方程组.(2)、规律探究:猜想关于、的方程组的解是.16. 如图,已知抛物线y=ax2+bx-4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-2,0),直线BC的解析式为y= x-4.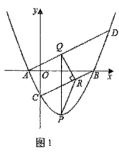
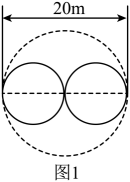
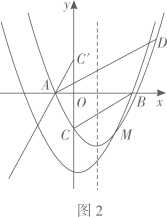 (1)、求抛物线的解析式;(2)、如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标;(3)、如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2 个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.17. 中学原计划在一个直径为20米的圆形场地内修建圆形花坛(花坛指的是图中实线部分),为使花坛修得更加美观、有特色,决定向全校征集方案,在众多方案中最后选出三种方案:
(1)、求抛物线的解析式;(2)、如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标;(3)、如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2 个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.17. 中学原计划在一个直径为20米的圆形场地内修建圆形花坛(花坛指的是图中实线部分),为使花坛修得更加美观、有特色,决定向全校征集方案,在众多方案中最后选出三种方案:方案A:如图1所示,先画一条直径,再分别以两条半径为直径修两个圆形花坛;
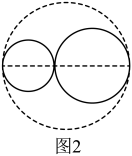
方案B:如图2所示,先画一条直径,然后在直径上取一点,把直径分成2:3的两部分,再以这两条线段为直径修两个圆形花坛;
方案C:如图3所示,先画一条直径,然后在直径上任意取四点,把直径分成5条线段,再分别以这5条线段为直径修5个圆形花坛.
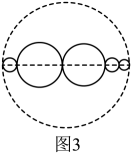 (1)、如果按照方案A修,修的花坛的周长是 .(2)、如果按照方案B修,与方案A比,省材料吗?为什么?(3)、如果按照方案C修,学校要求在8小时内完成,甲工人承包了此项工程,他做了4小时后,发现不能完成任务,就请乙来帮忙,乙的效率是甲的 , 乙加入后,甲的效率也提高了 , 结果正好按时完成任务,若修1米花坛可得到10元钱,修完花坛后,甲可以得到多少钱?(取3)18. 临近2022年春节,西安疫情形势较为严峻,对确诊病例所在地区实行区域管控,严格履行疫情防控措施为防范疫情,某校欲购置规格分别为300mL和500mL的甲、乙两种消毒液若干瓶,已知购买2瓶甲种和1瓶乙种消毒液需要61元,购买3瓶甲种和4瓶乙种消毒液需要154元。(1)、求甲,乙两种消毒液的单价;(2)、为节约成本,该校购买散装消毒液进行分装,现需将11.2L的消毒液全部装人最大容量分别为300mL和500mL的两种空瓶中(每瓶均装满),若分装时平均每瓶需损耗20mL,请问如何分能使总损耗最小?求出此时需要的两种空瓶的数量.19. 为了响应“践行核心价值观,传递青春正能量”的号召,小颖决定走入社区号召大家参加“传递正能量志愿服务者”.假定从一个人开始号召,每一个人每周能够号召相同的m个人参加,被号召参加的人下一周会继续号召,两周后,将有121人被号召成为“传递正能量志愿服务者”.(1)、求出m的值;(2)、经过计算后,小颖、小红、小丽三人开始发起号召,但刚刚开始,他们就发现了问题,实际号召过程中,不是每一次号召都可以成功,而他们三人的成功率也各不相同,已知小红的成功率比小颖的两倍少10%,第一周后小丽比小颖多号召2人,三人一共号召17人,其中小颖号召了n人.请分别求出他们三人号召的成功率.20. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)、如果按照方案A修,修的花坛的周长是 .(2)、如果按照方案B修,与方案A比,省材料吗?为什么?(3)、如果按照方案C修,学校要求在8小时内完成,甲工人承包了此项工程,他做了4小时后,发现不能完成任务,就请乙来帮忙,乙的效率是甲的 , 乙加入后,甲的效率也提高了 , 结果正好按时完成任务,若修1米花坛可得到10元钱,修完花坛后,甲可以得到多少钱?(取3)18. 临近2022年春节,西安疫情形势较为严峻,对确诊病例所在地区实行区域管控,严格履行疫情防控措施为防范疫情,某校欲购置规格分别为300mL和500mL的甲、乙两种消毒液若干瓶,已知购买2瓶甲种和1瓶乙种消毒液需要61元,购买3瓶甲种和4瓶乙种消毒液需要154元。(1)、求甲,乙两种消毒液的单价;(2)、为节约成本,该校购买散装消毒液进行分装,现需将11.2L的消毒液全部装人最大容量分别为300mL和500mL的两种空瓶中(每瓶均装满),若分装时平均每瓶需损耗20mL,请问如何分能使总损耗最小?求出此时需要的两种空瓶的数量.19. 为了响应“践行核心价值观,传递青春正能量”的号召,小颖决定走入社区号召大家参加“传递正能量志愿服务者”.假定从一个人开始号召,每一个人每周能够号召相同的m个人参加,被号召参加的人下一周会继续号召,两周后,将有121人被号召成为“传递正能量志愿服务者”.(1)、求出m的值;(2)、经过计算后,小颖、小红、小丽三人开始发起号召,但刚刚开始,他们就发现了问题,实际号召过程中,不是每一次号召都可以成功,而他们三人的成功率也各不相同,已知小红的成功率比小颖的两倍少10%,第一周后小丽比小颖多号召2人,三人一共号召17人,其中小颖号召了n人.请分别求出他们三人号召的成功率.20. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下: (1)、建立函数模型
(1)、建立函数模型设矩形相邻两边的长分别为x,y,由矩形的面积为4,得 ,即 ;由周长为 ,得 ,即 .满足要求的 应是两个函数图象在第象限内交点的坐标.
(2)、画出函数图象函数 的图象如图所示,而函数 的图象可由直线 平移得到.请在同一直角坐标系中直接画出直线 .
(3)、平移直线 ,观察函数图象①当直线平移到与函数 的图象有唯一交点 时,周长 的值为▲ ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)、得出结论若能生产出面积为4的矩形模具,则周长m的取值范围为.
21. 如图, 是边长为 的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是 ,当点 到达点 时,P,Q两点停止运动,设点 的运动时间为 ,解答下列问题: (1)、求 的面积.(2)、当 为何值时, 是直角三角形?(3)、是否存在某一时刻 ,使四边形APQC的面积是 面积的 ?如果存在,求出 的值;如果不存在,请说明理由.22. 已知数轴上两点A,B对应的数分别是 ,4,P、M、N为数轴上的三个动点,点M从B点出发速度为每秒2个单位,点N从A点出发速度为M点的2倍,点P从原点出发速度为每秒1个单位.
(1)、求 的面积.(2)、当 为何值时, 是直角三角形?(3)、是否存在某一时刻 ,使四边形APQC的面积是 面积的 ?如果存在,求出 的值;如果不存在,请说明理由.22. 已知数轴上两点A,B对应的数分别是 ,4,P、M、N为数轴上的三个动点,点M从B点出发速度为每秒2个单位,点N从A点出发速度为M点的2倍,点P从原点出发速度为每秒1个单位. (1)、线段 之间的距离为个单位长度.(2)、若点M向左运动,同时点N向右运动,求多长时间点M与点N相遇?(3)、若点M、N、P同时都向右运动,求多长时间点P到点M,N的距离相等?23. 如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
(1)、线段 之间的距离为个单位长度.(2)、若点M向左运动,同时点N向右运动,求多长时间点M与点N相遇?(3)、若点M、N、P同时都向右运动,求多长时间点P到点M,N的距离相等?23. 如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.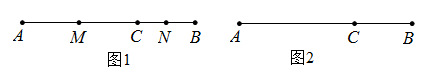 (1)、求线段MN的长度.(2)、根据第(1)题的计算过程和结果,设AC=a,BC=b,其他条件不变,求MN的长度.(3)、动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动.设点P的运动时间为t(s).当C、P、Q三点中,有一点恰好是以另外两点为端点的线段的中点时,直接写出时间t.24. 如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线的下方.
(1)、求线段MN的长度.(2)、根据第(1)题的计算过程和结果,设AC=a,BC=b,其他条件不变,求MN的长度.(3)、动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动.设点P的运动时间为t(s).当C、P、Q三点中,有一点恰好是以另外两点为端点的线段的中点时,直接写出时间t.24. 如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线的下方. (1)、将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为度;(2)、在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
(1)、将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为度;(2)、在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
(3)、将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的进程中,假如第t秒时,OA,OC,ON三条射线构成相等的角,求此时的值为多少?(直接写出答案)25. 定义“※”运算,观察下列运算:(+2)※(+13)=15,(-10)※(-12)=22;
(-5)※(+13)=-18,(+8)※(-10)=-18;
0※(+13)=-13,(-10)※0=10.
(1)、请你认真思考上述运算,归纳“※”运算的法则:两数进行“※”运算时,同号 , 异号 , 并把绝对值;
特别地,0和任何数进行“※”运算或任何数和0进行“※”运算,都得这个数的.
(2)、计算:(-15)※[0※(+7)].(3)、若(2※a)×3+2=4a,求a的值.26. 阅读理解:在钟面上,把一周分成12个大格,每个大格分成5个小格,所以每个大格对应的是30°角,每个小格对应的是6°角,时针每分钟转过的角度是0.5度,分针每分针转过的角度是6度.解决问题:
 (1)、当时钟的时刻是8:30时,求此时分针与时针所夹的锐角的度数.(2)、8:00开始几分钟后分针第一次追上时针.(3)、设在8:00时,分针的位置为OA,时针的位置为OB,运动后的分针为OP,时针为OQ.问:在8:00~9:00之间,从8:00开始运动几分钟,OB,OP,OQ这三条射线,其中一条射线是另外两条射线所夹的角的平分线?27. 如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠D=30°)的直角顶点放在点O处,一边OE在射线OA上,另一边OD与OC都在直线AB的上方.
(1)、当时钟的时刻是8:30时,求此时分针与时针所夹的锐角的度数.(2)、8:00开始几分钟后分针第一次追上时针.(3)、设在8:00时,分针的位置为OA,时针的位置为OB,运动后的分针为OP,时针为OQ.问:在8:00~9:00之间,从8:00开始运动几分钟,OB,OP,OQ这三条射线,其中一条射线是另外两条射线所夹的角的平分线?27. 如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠D=30°)的直角顶点放在点O处,一边OE在射线OA上,另一边OD与OC都在直线AB的上方. (1)、将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周,如图2,经过t秒后,OD恰好平分∠BOC.
(1)、将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周,如图2,经过t秒后,OD恰好平分∠BOC.①此时t的值为 ▲ ;(直接填空)
②此时OE是否平分∠AOC?请说明理由;
(2)、在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠DOE?请说明理由;(3)、在(2)问的基础上,经过多长时间OC平分∠DOB?请画图并说明理由.28. 平面直角坐标系中,点A(x,y),且x2-8x+16+ =0,△ABC是以AB为斜边的等腰直角三角形(点A、B、C逆时针排列).
=0,△ABC是以AB为斜边的等腰直角三角形(点A、B、C逆时针排列).

 (1)、直接写出点A的坐标是;(2)、如图1,已知点B(0,n)且0<n<4,连接OC. 求四边形ABOC的面积;
(1)、直接写出点A的坐标是;(2)、如图1,已知点B(0,n)且0<n<4,连接OC. 求四边形ABOC的面积;
(3)、如图2,已知点B(m,n)且0<m<4,0<n<4,过点A作AD⊥y轴于D,连接OB,M为OB的中点,连接DM、CM. 求证:DM⊥CM.
29. 如图为半圆形计时器, 指针 绕点 从 开始逆时针向 旋转, 速度为 每秒, 指针 绕点 从 开始先顺时针向 旋转, 到达 后再逆时针向回旋转, 速度为 每秒, 两指针同时从起始位置出发, 当 到达时, 两针都停止旋转。设旋转时间为 秒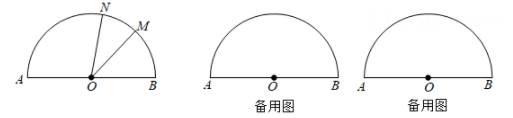 (1)、求 为何值时 与 首次重合;(2)、求 (用含 的代数式表示);(3)、直接写出 时 的值为.30. 如图,点 , 是数轴上两点,点表示的数为 , . 动点 , 分别从 , 出发,点以每秒2个单位长度的速度沿数轴向右匀速运动,点以每秒1个单位长度的速度沿数轴向左匀速运动,设运动时间为秒.
(1)、求 为何值时 与 首次重合;(2)、求 (用含 的代数式表示);(3)、直接写出 时 的值为.30. 如图,点 , 是数轴上两点,点表示的数为 , . 动点 , 分别从 , 出发,点以每秒2个单位长度的速度沿数轴向右匀速运动,点以每秒1个单位长度的速度沿数轴向左匀速运动,设运动时间为秒. (1)、数轴上点表示的数是 .(2)、求数轴上点 , 表示的数(用含t的式子表示).(3)、若点和同时出发,t为何值时,这两点相遇?(4)、若点比点迟2秒钟出发,则点出发几秒时,点和点刚好相距5个单位长度?
(1)、数轴上点表示的数是 .(2)、求数轴上点 , 表示的数(用含t的式子表示).(3)、若点和同时出发,t为何值时,这两点相遇?(4)、若点比点迟2秒钟出发,则点出发几秒时,点和点刚好相距5个单位长度?