2022年初中数学浙教版七年级下册5.5分式方程能力阶梯训练——普通版

试卷更新日期：2022-05-31 类型：同步测试

进入出卷网下载

一、单选题

1. 若分式方程 $\frac{2 (x + a)}{a (x - 1)} = - \frac{8}{5}$ 的解为 $x = - \frac{1}{5}$ ，则 $a$ 等于（）

A、 $\frac{5}{6}$ B、5 C、 $- \frac{5}{6}$ D、-5

查看试题解析
2. 甲、乙两人同时从A地出发，骑自行车到B地，已知A，B两地的距离为30 km，甲每小时比乙多走3 km，并且甲比乙先到20 min.设乙每小时走： km，则可列方程为（）

A、 $\frac{30}{x} - \frac{30}{x - 3} = \frac{1}{3}$ B、 $\frac{30}{x} - \frac{30}{x + 3} = \frac{1}{3}$ C、 $\frac{30}{x + 3} - \frac{30}{x} = \frac{1}{3}$ D、 $\frac{30}{x - 3} - \frac{30}{x} = \frac{1}{3}$

查看试题解析
3. 下列方程中，是分式方程的个数是（）
① $\frac{x + 1}{3} = 1$ ，② $\frac{3}{x + 1} = 4$ ，③ $\frac{x^{2} - 1}{x + 1} = 1$ ，④ $\frac{x}{2} + \frac{x - 1}{3} = 2$ ，⑤ $\frac{x + 1}{π} + 2 = x$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 代数式 $\frac{x - 1}{3}$ 的值等于1时，x的值是（）

A、3 B、1 C、4 D、﹣1

查看试题解析
5. 方程 $\frac{x}{2} - \frac{x - 1}{6} = 1$ ，去分母正确的是（）

A、 $6 x - (x - 1) = 6$ B、 $3 x - (x - 1) = 1$ C、 $3 x - (x - 1) = 6$ D、 $3 x - x - 1 = 6$

查看试题解析

二、填空题

6. 若关于 $x$ 的分式方程 $\frac{3 x + 2}{x - 1} = \frac{m}{x - 1}$ 有增根，则增根是.

查看试题解析
7. 已知点A，B在数轴上位置如图，它们所对应的数分别是 $- 2 ， \frac{x - 7}{3 x - 1}$ ，且点A，B到原点的距离相等，则 $x$ 的值为.

查看试题解析
8. 已知式子 $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ ，用 $R_{1} ， R_{2}$ 的代数式表示 $R$ ，则 $R =$ .

查看试题解析
9. 某次列车平均提速 $v km / h$ ，用相同的时间，列车提速前行驶 $s km$ ，提速后比提速前多行驶 $50 m$ .设提速前列车的平均速度是 $x km / h$ .根据题意分别列出下列四个方程：① $\frac{s}{x} = \frac{s + 50}{x + v}$ ；② $\frac{s}{x + v} = \frac{s + 50}{x}$ ；③ $\frac{x}{x + v} = \frac{s}{s + 50}$ ；④ $\frac{s}{x} = \frac{50}{v}$ .则其中正确的方程有.(填序号)

查看试题解析
10. 为了帮助遭受自然灾害的地区重建家园，某学校号召同学们自愿捐款.已知第一次捐款总额为4800元，第二次捐款总额为5000元，第二次捐款人数比第一次多20，而且两次人均捐款额相等，则第一次捐款有人.

查看试题解析
11. 下列是解分式方程 $\frac{2}{x + 1} + \frac{3}{x - 1} = \frac{6}{x^{2} - 1}$ 的步骤
①方和两边都乘 $(x + 1) (x - 1)$ ；

②得整式方程 $2 (x - 1) + 3 (x + 1) = 6$ ；

③解得 $x = 1$ ；

④所以原分式方程的解是 $x = 1$ .

错误的一步是.(填序号)

查看试题解析
12. 当 $x =$ 时.代数式 $\frac{x - 5}{x - 8}$ 和 $\frac{4 - 2 x}{8 - x}$ 的值互为相反数

查看试题解析

三、综合题

13. 某市轻轨3号线的一项挖土工程招标时，接到甲.乙两个工程队的投标书，每施工一天，需付甲工程队工程款2.1万元，付乙工程队工程款1.5万元，工程领导小组根据甲、乙两队的投标书测算，可有三种施工方案：
方案一：甲队单独完成这项工程，刚好按规定工期完成.

方案二：乙队单独完成这项工程要比规定工期多用5天.

方案三：若由甲，乙两队合作做4天，剩下的工程由乙队单独做，也正好按规定工期完工.

(1)、请你求出完成这项工程的规定时间；

(2)、如果你是工程领导小组的组长，为了节省工程款，同时又能如期完工，你将选择哪一种方案?说明理由.

查看试题解析
14. 长春市政府计划对城区某道路进行改造，现安排甲、乙两个工程队共同完成．已知甲队的工作效率是乙队工作效率的 $1.5$ 倍，甲队改造 $480$ 米的道路比乙队改造同样长的道路少用 $2$ 天．

(1)、求乙工程队每天能改造道路的长度；

(2)、若甲队工作一天的改造费用为 $8$ 万元，乙队工作一天的改造费用为 $6$ 万元，如需改造的道路全长为 $8000$ 米，如果安排甲、乙两个工程队同时开工，并一起完成这项城区道路改造，求改造该段道路所需的总费用．

查看试题解析
15. 某商贩用960元从批发市场购进某种水果销售，由于春节临近，几天后他又用1800元以每千克比第一次高出2元的价格购进这种水果，第二次购进水果的数量是第－次购进数量的1.5倍，设第一次购进水果的数量为x千克.

(1)、用含x的式子表示：第二次购进水果为千克，第一次购进水果的单价为元/千克；

(2)、该商贩两次购进水果各多少千克？

(3)、若商贩将两次购进的水果均按每千克15元的标价进行销售，为了在春节前将水果全部售完，在按标价售出m (100≤m≤200)千克后将余下部分每千克降价a (a为正整数)元全部售出，共获利为1440元，则a的值为(直接写出结果) .

查看试题解析
16. 为了迎接新学期的到来，某文化用品商店分两批购进同样的书包，提供给新入学的学生购买使用．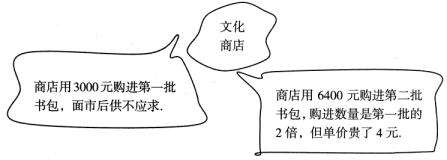

(1)、第二批购进书包的单价是多少元？

(2)、两批书包的销售价格都是90元，当第二批书包投放市场后立即产生了滞销，商店以进价的八五折优惠促销，全部售出后，商店是盈利还是亏损？

查看试题解析
17. 某校推行“新时代好少年•红心向党”主题教育读书工程建设活动，原计划投资10000元建设几间青少年党史“读书吧”，为了保证“读书吧”的建设的质量，实际每间“读书吧”的建设费用增加了10%，实际总投资为15400元，并比原计划多建设了2间党史“读书吧”.

(1)、原计划每间党史“读书吧”的建设费用是多少元？

(2)、该校实际共建设了多少间青少年党史“读书吧”？

查看试题解析
18. 为了响应打赢“蓝天保卫战”的号召，黄老师上下班的交通方式由驾车改为骑自行车，黄老师家距离学校的路程是9千米，在相同的路线上，驾车的平均速度是骑自行车的平均速度的3倍，所以黄老师每天上班要比开车早出发20分钟，才能按原驾车的时间到达学校．

(1)、求黄老师驾车的平均速度；

(2)、据测算，黄老师的汽车在上下班行驶过程中平均每小时碳排放量约为2.4千克，按这样计算，求黄老师一天（按一个往返计算）可以减少的碳排放量．

查看试题解析
19. 为厉行节能减排，倡导绿色出行，“共享单车”登陆某市中心城区，某公司拟在甲、乙两个街道社区投放一批“共享单车”，这批自行车包括A，B两种不同款型．请解决下列问题：

(1)、该公司早期在甲街区进行了试点投放，共投放A，B两型自行车各50辆，投放成本共计20500元，其中B型车的成本单价比A型车高10元，求A，B两型自行车的成本单价各是多少？

(2)、该公司决定采取如下投放方式：甲街区每1000人投放a辆“共享单车”，乙街区每1500人投放2a辆“共享单车”，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有12万人，试求a的值．

查看试题解析
20. 某工厂计划在规定时间内生产24000个零件．若每天比原计划多生产30个零件，则在规定时间内可以多生产300个零件．

(1)、求原计划每天生产的零件个数和规定的天数

(2)、为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%．按此测算，恰好提前两天完成24000个零件的生产任务，求原计划安排的工人人数．

查看试题解析

2022年初中数学浙教版七年级下册5.5分式方程 能力阶梯训练——普通版

一、单选题

二、填空题

三、综合题

2022年初中数学浙教版七年级下册5.5分式方程能力阶梯训练——普通版