山东省烟台莱州市2022年中考一模数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 下列各数: , , 0, , , 其中比-3小的数有( )A、1个 B、2个 C、3个 D、4个2. 在下列历届冬奥会会徽中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2022年1月28日,北京冬奥组委发布《北京冬奥会低碳管理报告(赛前)》,根据本次“绿色办奥”理念,以及疫情下筹办和举办北京冬奥会的实际情况,修订后的基准线排放量约为130.6万吨二氧化碳当量,其中“130.6万”用科学记数法表示为( )A、 B、 C、 D、4. 某运动会颁奖台如图所示,它的主视图是( )
3. 2022年1月28日,北京冬奥组委发布《北京冬奥会低碳管理报告(赛前)》,根据本次“绿色办奥”理念,以及疫情下筹办和举办北京冬奥会的实际情况,修订后的基准线排放量约为130.6万吨二氧化碳当量,其中“130.6万”用科学记数法表示为( )A、 B、 C、 D、4. 某运动会颁奖台如图所示,它的主视图是( )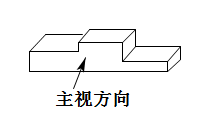 A、
A、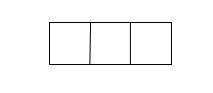 B、
B、 C、
C、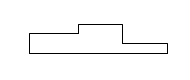 D、
D、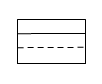 5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,点I是的内心,若 , 则等于( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,点I是的内心,若 , 则等于( ) A、50° B、52° C、54° D、56°7. 已知抛物线与x轴的一个交点为 , 则代数式的值为( )A、2020 B、2021 C、2022 D、20238. 如图,正方形 的边 , 和 都是以 为半径的圆弧,阴影两部分的面积分别记为 和 ,则 - 等于( )
A、50° B、52° C、54° D、56°7. 已知抛物线与x轴的一个交点为 , 则代数式的值为( )A、2020 B、2021 C、2022 D、20238. 如图,正方形 的边 , 和 都是以 为半径的圆弧,阴影两部分的面积分别记为 和 ,则 - 等于( ) A、 B、 C、 D、9. 如图,AB是半圆O的直径,以弦AC为折痕折叠后,恰好经过点O,则等于( )
A、 B、 C、 D、9. 如图,AB是半圆O的直径,以弦AC为折痕折叠后,恰好经过点O,则等于( ) A、120° B、125° C、130° D、145°10. 已知a,b,c分别是的三条边,c为斜边,我们把形如的一次函数称为“勾股一次函数”.若点P(1,)在“勾股一次函数”的图象上,且的面积等于4,则c的值为( )A、2 B、4 C、 D、
A、120° B、125° C、130° D、145°10. 已知a,b,c分别是的三条边,c为斜边,我们把形如的一次函数称为“勾股一次函数”.若点P(1,)在“勾股一次函数”的图象上,且的面积等于4,则c的值为( )A、2 B、4 C、 D、二、填空题
-
11. 已知关于x的分式方程 的解为正数,则 的取值范围为 .12. 已知关于x的不等式组至少有两个整数解,且存在以3,a,7为边的三角形,则a的整数解有个.13. 如图,以的半径为半径,自上的A点起,在圆上依次画弧截取点B,C,D,E,F.正方形EFGH的中心为 , 连接FA, , 则 .
 14. 如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB= S矩形ABCD , 则点P到A、B两点的距离之和PA+PB的最小值为 .
14. 如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB= S矩形ABCD , 则点P到A、B两点的距离之和PA+PB的最小值为 .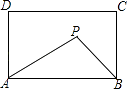 15. 如图,AB,CD是的直径,弦BE与CD交于点F,F为BE中点, . 若 , 则BC的长为 .
15. 如图,AB,CD是的直径,弦BE与CD交于点F,F为BE中点, . 若 , 则BC的长为 . 16. 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2022次,点B的落点依次为B1 , B2 , B3 , …,则B2022的坐标为 .
16. 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2022次,点B的落点依次为B1 , B2 , B3 , …,则B2022的坐标为 .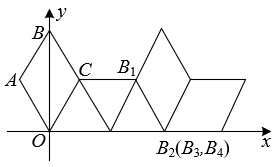
三、解答题
-
17. 先化简,再求值:
, 其中 .
18. 某校在七、八年级举行了“新冠疫情防控知识”调查活动,从七、八年级各随机抽取了10名学生进行比赛(百分制),比赛成绩整理、描述和分析如下(成绩得分用x表示,共分成四组:A. , B. , C. , D.):七年级10名学生的成绩是:95,84,99,89,99,86,100,80,89,99.
八年级10名学生的成绩在C组中的数据是:93,90,91.
现已画出了八年级抽取的学生成绩扇形统计图(如图),并列出了七、八年级抽取的学生竞赛成绩统计表(不完整).
年级
平均数
中位数
众数
极差
方差
七年级
53.6
八年级
92
100
19
41.1

根据以上信息,解答下列问题:
(1)、这次比赛中年级成绩更稳定;(2)、求出扇形统计图中的a的值;(3)、填写统计表中的空格;(4)、已知八年级只有2名学生考取了相同的分数,现在学校要随机选取2名满分的学生代表学校参赛,用画树状图或列表的方法求出恰好选到七、八年级各一名学生的概率.19. 如图,某大楼(DE)的顶部树有一块广告牌CD,实践小组在斜坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°.已知斜坡的坡比为 , 米,米.求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: , ) 20. 如图,在中, , 于点D,点M是BC的中点.求证: .
20. 如图,在中, , 于点D,点M是BC的中点.求证: . 21. 如图,直线与反比例函数的图象交于点 , 与x轴交于点B.平行于x轴的直线交反比例函数的图象于点M,交AB于点N,连接BM.
21. 如图,直线与反比例函数的图象交于点 , 与x轴交于点B.平行于x轴的直线交反比例函数的图象于点M,交AB于点N,连接BM. (1)、求m的值和反比例函数的表达式;(2)、当n为何值时,的面积最大?22. 如图,AB是外接圆的直径,圆心为点O,点C,D是圆上两点,且 , 连接CD交AB于点E.若 , 求的值.
(1)、求m的值和反比例函数的表达式;(2)、当n为何值时,的面积最大?22. 如图,AB是外接圆的直径,圆心为点O,点C,D是圆上两点,且 , 连接CD交AB于点E.若 , 求的值.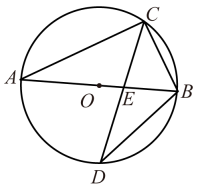 23. 党中央统一部署指挥全国的抗疫,各级政府统筹安排生产与民生,全民抗疫,同心同德.疫情期间,甲、乙两个蔬菜生产基地向A,B两疫情城市运送蔬菜,以解决民生问题.已知甲、乙两基地共有蔬菜500吨,其中甲基地蔬菜比乙基地少100吨,从甲、乙基地往A,B两城运蔬菜的费用如表.现A城需要蔬菜240吨,B城需要蔬菜260吨.
23. 党中央统一部署指挥全国的抗疫,各级政府统筹安排生产与民生,全民抗疫,同心同德.疫情期间,甲、乙两个蔬菜生产基地向A,B两疫情城市运送蔬菜,以解决民生问题.已知甲、乙两基地共有蔬菜500吨,其中甲基地蔬菜比乙基地少100吨,从甲、乙基地往A,B两城运蔬菜的费用如表.现A城需要蔬菜240吨,B城需要蔬菜260吨.甲基地
乙基地
A城
20元/吨
15元/吨
B城
25元/吨
30元/吨
(1)、甲、乙两个蔬菜生产基地各有蔬菜多少吨?(2)、设从乙基地运往B城蔬菜x吨,总运费为y元,求y与x之间的函数关系式,并写出自变量x的取值范围;(3)、由于开通新的线路,使乙基地运往B城的运费每吨减少元,其余路线运费不变.若总运费的最小值不小于10020元,求a的最大整数解?24. 如图,正方形ABCD中分别交BC,CD于点E,F,连接EF. (1)、如图①,若 , , 试求的度数;(2)、如图②,以点A为旋转中心,旋转 , 旋转时保持 . 当点E,F分别在边BC,CD上时,AE和AF是角平分线吗?如果是,请说出是哪两个角的平分线并给予证明;如果不是,请说明理由;(3)、如图③,在②的条件下,当点E,F分别在BC,CD的延长线上时,②中的结论是否成立?只需回答结论,不需说明理由.25. 如图①,在平面直角坐标系中,抛物线经过点 , 顶点为点B,点P为拋物线上的一个动点,l是过点且垂直于y轴的直线,连接PO.
(1)、如图①,若 , , 试求的度数;(2)、如图②,以点A为旋转中心,旋转 , 旋转时保持 . 当点E,F分别在边BC,CD上时,AE和AF是角平分线吗?如果是,请说出是哪两个角的平分线并给予证明;如果不是,请说明理由;(3)、如图③,在②的条件下,当点E,F分别在BC,CD的延长线上时,②中的结论是否成立?只需回答结论,不需说明理由.25. 如图①,在平面直角坐标系中,抛物线经过点 , 顶点为点B,点P为拋物线上的一个动点,l是过点且垂直于y轴的直线,连接PO. (1)、求抛物线的表达式,并求出顶点B的坐标;(2)、试证明:经过点O的与直线l相切;.(3)、如图②,已知点C的坐标为 , 是否存在点P,使得以点P,O及(2)中的切点为顶点的三角形与相似?若存在,求出P点的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式,并求出顶点B的坐标;(2)、试证明:经过点O的与直线l相切;.(3)、如图②,已知点C的坐标为 , 是否存在点P,使得以点P,O及(2)中的切点为顶点的三角形与相似?若存在,求出P点的坐标;若不存在,请说明理由.