山东省烟台市芝罘区2022年中考一模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. -2022的相反数是（）

A、 $- 2022$ B、 $\frac{1}{2022}$ C、2022 D、 $- \frac{1}{2022}$

查看试题解析
2. 下面的图形是用数学家名字命名的，其中是轴对称图形，但不是中心对称图形的是（）

A、科克曲线 B、笛卡尔心形线 C、赵爽弦图 D、斐波那契螺旋线

查看试题解析
3. 如图几何体是一个三棱柱的示意图，该几何体的俯视图是（　　）

A、 B、 C、 D、

查看试题解析
4. 2021年第一季度，全国规模以上文化及相关产业实现营业收入25498亿元，文化及相关产业发展基本恢复到疫情前水平数据25498亿用科学记数法表示为（　　）

A、 $2.5498 \times 1 0^{4}$ B、 $2.5498 \times 1 0^{12}$ C、 $2.5498 \times 1 0^{13}$ D、 $25.498 \times 1 0^{11}$

查看试题解析
5. 在螳螂的示意图中，AB∥DE，△ABC是等腰三角形，∠ABC＝124°，∠CDE＝72°，则∠ACD＝（）

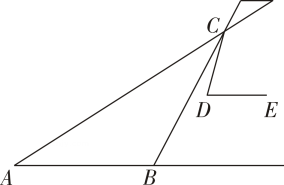A、16° B、28° C、44° D、45°

查看试题解析
6. 关于x的方程 $x^{2} - 2 x - 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
7. 某校交响乐团有90名成员，下表是合唱团成员的年龄分布统计表：对于不同的x ，下列关于年龄的统计量不会发生改变的是（　　）

年龄（单位：岁）

13

14

15

16

17

频数（单位：名）

17

29

x

26﹣x

18

A、平均数、中位数 B、平均数、方差 C、众数、中位数 D、众数、方差

查看试题解析
8. 若关于x的方程 $\frac{2}{x - 2} + \frac{m}{2 - x} = 2$ 的解为正数，则m的取值范围是（　　）

A、 $m < 6$ B、 $m > 6$ C、 $m > 6$ 且 $m \neq 10$ D、 $m < 6$ 且 $m \neq 2$

查看试题解析
9. 如图，⊙O是△ABC的外接圆，AB是直径，过点C的切线交AB的延长线于点D，若 $t a n ∠ B C D = \frac{1}{2}$ ， $A D = 8 c m$ ，则⊙O的半径长为（　　）

A、2cm B、 $\sqrt{5}$ cm C、3cm D、 $\frac{3}{2} \sqrt{5}$ cm

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，图象过点 $(- 1 ， 0)$ ，对称轴为直线 $x = 2$ ，下列结论：① $4 a + b = 0$ ；② $9 a + c > - 3 b$ ；③ $7 a - 3 b + 2 c > 0$ ；④若方程 $a (x + 1) (x - 5) = - 3$ 的两根为 $x_{1}$ 和 $x_{2}$ ，且 $x_{1} < x_{2}$ ，则 $x_{1}^{2} + x_{2}^{2} > 26$ ．其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 函数y＝ $\frac{\sqrt{x - 2}}{x}$ 中，自变量x的取值范围是．

查看试题解析
12. 分解因式 $a m^{2} - a$ 的结果是．

查看试题解析
13. 如图，果农将苹果树种在正方形的果园．为了保护苹果树不被风吹，他在苹果树的周围种针叶树，根据图中规律，该果农计划种100棵苹果树，需要种针叶树的棵数为．

查看试题解析
14. 如图，菱形ABCD的顶点C在等边△BEF的边BF上，点E在AB的延长线上，连接DE，过点C作EF的平行线交DE于点G．若 $A B = 3$ ， $B E = 5$ ，则CG的长度是．

查看试题解析
15. 如图，在△ABC中，∠ACB=90°，AC=BC=4，将△ABC折叠，使点A落在BC边上的点D处，EF为折痕，若AE＝3，则sin∠BFD的值为

查看试题解析
16. 如图，抛物线 $y = \frac{1}{4} x^{2} - 4$ 与x轴交于A、B两点，P是以点C（0，3）为圆心，2为半径的圆上的动点，Q是线段PA的中点，连接OQ．则线段OQ的最大值是．

查看试题解析

三、解答题

17. 化简： $（ \frac{x}{x - 1} - \frac{1}{x^{2} - x}) \div \frac{x^{2} + 2 x + 1}{x^{2}}$ ，并从﹣1，0，1，2中选择一个合适的数求代数式的值．

查看试题解析
18. 张老师为了解学生完成数学课前预习的具体情况，对部分学生进行了跟踪调查，并将调查结果分为四类，A：很好；B：较好；C：一般：D；较差．制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

(1)、C类中女生有名，将条形统计图补充完整；

(2)、若该校九年级共有女生180名，则九年级女生完成数学作业达到很好和较好的大约多少人？

(3)、为了共同进步，张老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好性别相同的概率．

查看试题解析
19. 心理学家研究发现，在一节45分钟的课中，学生的注意力随教师讲课的时间的变化而变化，开始学生的注意力逐渐增强，中间学生的注意力保持稳定的状态，随后开始分散，经实验学生的注意力指数y随时间x（分钟）的变化规律如图所示．

(1)、一位教师为了达到最好的上课效果，准备课前复习，要求学生的注意力指数至少达到30时，开始上新课，问他应该复习多长时间？

(2)、如果（1）的这位教师本节新课内容需要22分钟，为了使学生的听课效果最好，问这位教师能否在学生听课效果最好时，讲完新课内容？

查看试题解析
20. 某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米．自2018年初开始实施后，实际每年绿化面积是原计划的1.5倍，这样可提前4年完成任务．

(1)、实际每年绿化面积为多少万平方米？

(2)、为加大创建力度，市政府决定从2021年起加快绿化速度，要求不超过3年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？

查看试题解析
21. 如图，在山坡BC坡顶的平台CD上竖直立有一根旗杆MN，已知山坡BC的坡度为3：4．小明站在A处测得旗杆顶端M的仰角是 $37 °$ ，向前步行3米到达B处（ $A B = 3$ 米），再延斜坡BC步行5米至平台点C处（ $B C = 5$ ），测得点M的仰角是 $50 °$ ，若A、B、C、D、M、N在同一平面内，且A，B和C，D，N分别在同一水平线上，小明的眼睛距离脚底的高度 $A E = C F = 1.6$ 米，求旗杆MN的高度．（结果精确到0.1米，参考数据： $s i n 37 ° \approx 0.6$ ， $c o s 37 ° \approx 0.8$ ， $t a n 37 ° \approx 0.75$ ， $s i n 50 ° \approx 0.77$ ， $c o s 50 ° \approx 0.64$ ， $t a n 50 ° ≈ 1.20$ ）

查看试题解析
22. 等腰三角形ABC， $A B = A C$ ， $C D ⊥ A B$ 于点D， $A E ⊥ B C$ 于点E，AE、CD交于点F，⊙O为△ADF的外接圆，连接DE．

(1)、求证：DE是⊙O的切线：

(2)、若 $C F ＝ 5$ ， $D F ＝ 3$ ，求⊙O的直径．

查看试题解析
23. 如图，抛物线 $y_{1} = a x^{2} - 6 a x + c (a \neq 0)$ 与x轴交于点A，B（点A在点B的右侧），与y轴交于点C， $O B = 2$ ，连接BC，AC，设AC关系式为 $y_{2} = k x + b$ ， $t a n ∠ O B C = 2$ ．

(1)、求抛物线的解析式；

(2)、点D是直线AC下方抛物线上一点， $D E ⊥ A C$ 于点E， $D F ⊥ x$ 轴于点F，DF与AC交于点G．
①当 $Δ D E G ≌ Δ A F G$ 时，求点D的横坐标；
②当△CDG是等腰三角形时，直接写出点D的坐标．

查看试题解析
24. 【问题解决】
如图1， $∠ A O B = 120 °$ ，点C是∠AOB平分线上一点，点D在射线OA上，将射线CD绕点C逆时针旋转 $60 °$ 与OB交于点E．
求证：

(1)、 $C D = C E$ ；

(2)、 $O D + O E = O C$ ．

(3)、【变式探究】
图2， $∠ A O B = 90 °$ ，点C是∠AOB平分线上一点，点D在射线OA上，将射线CD绕点C逆时针旋转 $90 °$ 与OB交于点E．填空：此时线段OD、OE、OC之间的数量关系是．

(4)、【拓展提升】
图3，矩形ABCD中， $A B = 11$ ， $A D = 12$ ， E为AD中点，点F在AB上，且 $A F = A E$ ，连接CF，作 $E H ⊥ C F$ 于H，连接AH，求线段AH的长度．

查看试题解析

年龄（单位：岁）	13	14	15	16	17
频数（单位：名）	17	29	x	26﹣x	18