山东省烟台市龙口市2022年中考一模数学试题

试卷更新日期：2022-05-31 类型：中考模拟

进入出卷网下载

一、单选题

1. －5的相反数是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、5 D、-5

查看试题解析
2. 如图所示，几何体的俯视图为（）

A、 B、 C、 D、

查看试题解析
3. 实数a，b在数轴上的对应点的位置如图所示，下列结论正确的是（）

A、a＞-2 B、b-a＜0 C、a＜b D、a+b＞0

查看试题解析
4. 围棋起源于中国，古代称之为“弈”，至今已有4 000多年的历史．以下是在棋谱中截取的四个部分，由黑白棋子摆成的图案既不是轴对称图形又不是中心对称的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，在四边形ABCD中，AD∥BC，BA⊥CA，垂足为A，若∠B=40°，则∠DAC等于（）

A、40° B、45° C、50° D、55°

查看试题解析
6. 若用我们数学课本上采用的科学计算器计算sin36 $°$ 18＇，按键顺序正确的是（）

A、 B、 C、 D、

查看试题解析
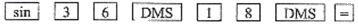7. “埃”是晶体学、原子物理、超显微结构等常用的长度单位，1长度单位“埃”，等于一亿分之一厘米．一亿分之一用科学记数法表示为（）

A、 $1 \times 1 0^{- 8}$ B、 $1 \times 1 0^{- 9}$ C、 $1 \times 1 0^{8}$ D、 $1 \times 1 0^{9}$

查看试题解析
8. 某班篮球兴趣小组10名队员进行定点投篮练习，每人投篮10次，将他们投中的次数进行统计，如下表：则关于这10名队员投中次数组成的数据，下列说法错误的是（）
投中次数
2
3
5
6
7
8
人数
1
2
3
2
1
1

A、平均数为5 B、中位数为5 C、众数为5 D、方差为2.7

查看试题解析
9. 如图，在直角坐标系xOy中，矩形EFGO的两边OE，OG在坐标轴上，以y轴上的某一点P为位似中心，作矩形ABCD，使其与矩形EFGO位似，若点B，F的坐标分别为（4，4），（-2，1），则位似中心P的坐标为（）

A、（0，1.5） B、（0，2） C、（0，2.5） D、（0，3）

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则下列结论中错误的是（）

A、 $a b c > 0$ B、函数的最大值为 $a - b + c$ C、当 $- 3 ⩽ x ⩽ 1$ 时， $y ⩾ 0$ D、 $4 a - 2 b + c < 0$

查看试题解析

二、填空题

11. 计算： $(- 1)^{0} - 2^{- 1} t a n^{2} 6 0^{°}$ = ．

查看试题解析
12. 如图，在两个同心圆中，四条直径把大圆分成八等份，若往圆面投掷飞镖，则飞镖落在黑色区域的概率是.

查看试题解析
13. 已知关于x的一元二次方程x²-4mx+3m²=0，若m＞0，且该方程较大的实数根为1，则m的值为．

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 1$ ， $B C = \frac{1}{2}$ .进行如下操作：
①以点C为圆心，以 $B C$ 的长为半径画弧交 $A C$ 于点D；

②以点A为圆心，以 $A D$ 的长为半径画弧交 $A B$ 于点E.

则点E是线段 $A B$ 的黄金分割点.

根据以上操作， $A E$ 的长为.

查看试题解析
15. 如图所示，在这个数据运算程序中，若开始输入的x的值为2，结果输出的是1，返回进行第二次运算，输出的是-4，…，则第2022次输出的结果是．

查看试题解析
16. 如图，在矩形ABCD中，AB＝3，AD＝2，以A为圆心，AD为半径作圆交AB于点E，F为 $\overset{⌢}{D E}$ 的中点，过F作CD的平行线，交AD于点G，交BC于点H，则阴影部分的面积为．

查看试题解析

三、解答题

17. 先化简，再求代数式 $\frac{1}{a} - \frac{a - 3}{a^{2} - 6 a + 9} \div \frac{a^{2} + a}{a - 3}$ 的值，其中 $a = 2 c o s 45 ° - 1$ ．

查看试题解析
18. 为了加快推进我国全民新冠病毒疫苗接种，在全国范围内构筑最大免疫屏障，各级政府积极开展接种新冠病毒疫苗的宣传工作．某社区印刷了若干套宣传海报（每套海报有A、B、C、D共四张），内容分别是志愿者小明和小亮利用休息时间到某小区张贴海报．

(1)、小明从一套海报中随机抽取一张，抽到B海报的概率是．

(2)、小明和小亮从同一套海报中各随机抽取一张，用列表法或画树状图法，求他们两个人中有一个人抽到D海报的概率．

查看试题解析

19. 促进青少年健康成长是实施“健康中国”战略的重要内容．为了引导学生积极参与体育运动，某校举办了一分钟跳绳比赛，随机抽取了40名学生一分钟跳绳的次数进行调查统计，并根据调查统计结果绘制了如下表格和统计图：

等级	次数	频率
不合格	100≤x $<$ 120	a
合格	120≤x $<$ 140	b
良好	140≤x $<$ 160
优秀	160≤x $<$ 180

请结合上述信息完成下列问题：

(1)、a＝， b＝；

(2)、请补全频数分布直方图；

(3)、在扇形统计图中，“良好”等级对应的圆心角的度数是；

(4)、若该校有2000名学生，根据抽样调查结果，请估计该校学生一分钟跳绳次数达到合格及以上的人数．

查看试题解析

20. 如图，一次函数y₁=kx+b的图象与x轴、y轴分别交于点A，B，与反比例函数y₂= $\frac{m}{x}$ （m＞0）的图象交于点C（1，2），D（2，n）．

(1)、分别求出两个函数的表达式；

(2)、连接OD，求△BOD的面积．

查看试题解析
21. 直播购物逐渐走进了人们的生活．某电商在抖音上对一款衬衫进行直播销售，销售信息如下：小王用1400元恰好购买了若干件此款衬衫，求小王购买该衬衫的件数．
购买件数
销售价格
不超过30件
单价40元
超过30件
每多买1件，购买的所有衬衫单价降低0.5元，
但单价不得低于30元

查看试题解析
22. 汽车盲区是指驾驶员位于驾驶座位置，其视线被车体遮挡而不能直接观察到的区域．如图，△ABC、△FED分别为汽车两侧盲区的示意图，已知视线PB与地面BE的夹角∠PBE=43°，视线PE与地面BE的夹角∠PEB=20°，点A，F分别为PB，PE与车窗底部的交点，AF∥BE，AC，FD垂直地面BE，A点到B点的距离AB=1.6m，求盲区中DE的长度．（参考数据：sin43°≈0.7，tan43°≈0.9，sin20°≈0.3，tan20°≈0.4）

查看试题解析
23. 如图，在Rt△ABC中，∠ACB=90°，延长CA到点D，以AD为直径作⊙O，交BA的延长线于点E，延长BC到点F，使BF=EF．

(1)、求证：EF是⊙O的切线；

(2)、若AC=2，CD=7，cos∠DAE= $\frac{4}{5}$ ，求EF的长．

查看试题解析
24. 在△ABC中，∠BAC=90°，AB=AC，点D在边BC上，BC=3BD，将线段DB绕点D顺时针旋转至DE，记旋转角为α（0°＜α＜180°），连接BE，CE，以CE为斜边在其一侧作等腰直角三角形CEF，连接AF．

(1)、如图1，求证：△CAF∽△CBE，并求出 $\frac{A F}{B E}$ 的值；

(2)、如图2，当B，E，F三点共线时，连接AE，请判断四边形AECF的形状，并说明理由．

查看试题解析
25. 如图1，在直角坐标系中，抛物线y=ax²+bx+4与x，y轴分别交于点A，B，C，已知点A的坐标是（4，0），OA=4OB，动点P在此抛物线上．

(1)、求抛物线的表达式；

(2)、是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，说明理由；

(3)、如图2，若动点P在第一象限内（图1中的其它条件不变），过点P作PE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线，垂足为F，连接EF，以线段EF的中点G为圆心，以EF为直径作⊙G，当⊙G最小时，求出点P的坐标．

查看试题解析

投中次数	2	3	5	6	7	8
人数	1	2	3	2	1	1