山东省潍坊市潍城区2022年中考二模数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 下列倡导节约的图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2022年4月18日,国家统计局发布初步核算,一季度国内生产总值270178亿元,同比增长4.8%,经济运行总体平稳.其中270178亿用科学记数法(精确到千亿位)表示为( )A、 B、 C、 D、3. 下列四个几何体分别是由5个相同的小正方体拼成的,其中从正面看到的图形与其他三个不同的是( )A、
2. 2022年4月18日,国家统计局发布初步核算,一季度国内生产总值270178亿元,同比增长4.8%,经济运行总体平稳.其中270178亿用科学记数法(精确到千亿位)表示为( )A、 B、 C、 D、3. 下列四个几何体分别是由5个相同的小正方体拼成的,其中从正面看到的图形与其他三个不同的是( )A、 B、
B、 C、
C、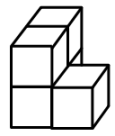 D、
D、 4. 如图,随机闭合4个开关 , , , 中的两个开关,能使电路接通的概率为( )
4. 如图,随机闭合4个开关 , , , 中的两个开关,能使电路接通的概率为( ) A、 B、 C、 D、5. 已知 , 则代数式的值为( )A、34 B、 C、26 D、6. 图,已知以的边AB为直径的经过点C,交于点D,连接BD.若 , 则的度数为( )
A、 B、 C、 D、5. 已知 , 则代数式的值为( )A、34 B、 C、26 D、6. 图,已知以的边AB为直径的经过点C,交于点D,连接BD.若 , 则的度数为( ) A、32° B、27° C、24° D、18°7. 如图,在中, , , 以点C为圆心,适当的长为半径作弧,分别交AC,BC于点E,F;分别以点E,F为圆心,大于的长为半径作弧,两弧交于点D;作射线CD.若点M为边BC上一动点,点N为射线CD上一动点,则的最小值为( )
A、32° B、27° C、24° D、18°7. 如图,在中, , , 以点C为圆心,适当的长为半径作弧,分别交AC,BC于点E,F;分别以点E,F为圆心,大于的长为半径作弧,两弧交于点D;作射线CD.若点M为边BC上一动点,点N为射线CD上一动点,则的最小值为( )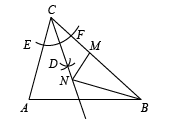 A、3 B、 C、4 D、8. 潍坊出租车采用阶梯式的计价收费办法如下表:
A、3 B、 C、4 D、8. 潍坊出租车采用阶梯式的计价收费办法如下表:行驶里程
计费方法
不超过3公里
起步价8元
超过3公里且不超过7公里的部分
每公里按标准租费收费
超过7公里且不超过25公里的部分
每公里再加收标准租费的50%
超过25公里且不超过100公里的部分
每公里再加收标准租费的75%
超过100公里的部分
每公里再加收标准租费的100%
说明:行驶里程不足1公里,按1公里计算;
行驶里程超过3公里时的标准租费为1.8元/公里.
若某人一次乘车费用为26元,那么行驶里程为( )
A、13公里 B、12公里 C、11公里 D、10公里二、多选题
-
9. 下列运算正确的是( )A、 B、 C、 D、10. 如果解关于x的分式方程时出现增根,则m的值可能为( )A、 B、 C、 D、111. 如图,抛物线过点 , 对称轴是直线 . 下列结论正确的是( )
 A、 B、 C、若关于x的方程有实数根,则 D、若和是抛物线上的两点,则当时,12. 如图,正方形ABCD,点E在边AB上,且AE:EB=2:3,过点A作DE的垂线,垂足为I,交BC于点F,交BD于点H,延长DC至G,使CG=DC,连接GI,EH.下列结论正确的是( )
A、 B、 C、若关于x的方程有实数根,则 D、若和是抛物线上的两点,则当时,12. 如图,正方形ABCD,点E在边AB上,且AE:EB=2:3,过点A作DE的垂线,垂足为I,交BC于点F,交BD于点H,延长DC至G,使CG=DC,连接GI,EH.下列结论正确的是( )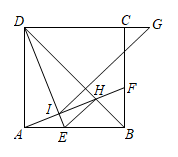 A、 B、 C、 D、
A、 B、 C、 D、三、填空题
-
13. .14. 用火柴棒按如图所示的方式摆大小不同的“ ”,依此规律,摆出第 个“ ”需用火柴棒根.
 15. 如图,将矩形纸片ABCD分别沿EF,EG折叠,点B,C恰好落在同一点P处.若 , , , 则图中阴影部分的面积为 .
15. 如图,将矩形纸片ABCD分别沿EF,EG折叠,点B,C恰好落在同一点P处.若 , , , 则图中阴影部分的面积为 . 16. 如图,在平面直角坐标系中,正比例函数与反比例函数的图像交于A,B两点,过A作y轴的垂线,交反比例函数的图象于点C,连接BC,若 , 则k的值为 .
16. 如图,在平面直角坐标系中,正比例函数与反比例函数的图像交于A,B两点,过A作y轴的垂线,交反比例函数的图象于点C,连接BC,若 , 则k的值为 .
四、解答题
-
17. 已知关于x的一元二次方程有 , 两个实数根.(1)、求m的取值范围;(2)、若 , 求 .18. 某学校为落实立德树人根本任务,使每个学生都能得到全面而个性的发展,特举办了“科学竞赛”活动,甲、乙两个班学生的成绩统计如下:
分数/分
50
60
70
80
90
100
甲班人数/人
2
5
10
18
14
1
乙班人数/人
4
4
16
4
18
4
活动规定:以60分为及格线,并分别设置了一、二、三等奖,100分为一等奖,90分为二等奖,80分为三等奖.小亮分别计算了两个班的平均分和方差,得: , , , . 请你根据以上材料回答下列问题.
(1)、甲、乙两个班的中位数和众数分别是多少?(2)、你认为甲、乙两个班哪个班的成绩更优秀?为什么?(3)、该校从得100分的两男三女5人中,随机选取2人参加教育局组织的竞赛,请你用列表或画树状图的方法,求出恰好选取一男一女参赛的概率.19. 一段东西方向的海岸线MN上,小明从点A测得灯塔C位于北偏西15°方向,向东走300米到达点B处,测得灯塔C位于北偏西60°方向. (1)、求点A到灯塔C的距离AC的长(结果保留根号)(2)、求灯塔C到海岸线MN的距离(结果保留根号).20. 某商场新进一种商品,进价为每件30元,日销售单价y(元)与销售天数t(天)之间存在如下关系:当时,y与t满足一次函数关系,部分数据如下表;当时,y保持90元不变.该商品的日销售量为m件,且 .
(1)、求点A到灯塔C的距离AC的长(结果保留根号)(2)、求灯塔C到海岸线MN的距离(结果保留根号).20. 某商场新进一种商品,进价为每件30元,日销售单价y(元)与销售天数t(天)之间存在如下关系:当时,y与t满足一次函数关系,部分数据如下表;当时,y保持90元不变.该商品的日销售量为m件,且 .销售天数t(天)
10
20
30
40
日销售单价y(元)
50
60
70
80
(1)、请求出y与t的函数表达式;(2)、设日销售利润为w元,销售该商品第几天时,当天的日销售利润最大,最大利润是多少元?(3)、该商品在50天之后的销售过程中,从第几天开始当天的日销售利润低于最大日销售利润的30%?21. 如图,以的边AB为直径的交BC于点D,延长CA交于点F,连接DF, , 取CF的中点G,连接DG并延长交BA的延长线于点E. (1)、求证:DE是的切线;(2)、若 , , 求AF的长.22. 已知抛物线于经过点 , 并与x轴交于另一点B,交y轴于点C,其对称轴为 .
(1)、求证:DE是的切线;(2)、若 , , 求AF的长.22. 已知抛物线于经过点 , 并与x轴交于另一点B,交y轴于点C,其对称轴为 .
 (1)、求抛物线的表达式;(2)、如图,点P是抛物线上位于直线BC上方的动点,过点P分别作x轴、y轴的平行线,交y轴于点D,交直线BC于点E,当取最大值时,求点P的坐标;(3)、已知点M为抛物线对称轴l上一动点,在抛物线上是否存在一点N,使得点M与点N关于直线BC对称,若存在,请求出点N的坐标;若不存在,请说明理由.23.
(1)、求抛物线的表达式;(2)、如图,点P是抛物线上位于直线BC上方的动点,过点P分别作x轴、y轴的平行线,交y轴于点D,交直线BC于点E,当取最大值时,求点P的坐标;(3)、已知点M为抛物线对称轴l上一动点,在抛物线上是否存在一点N,使得点M与点N关于直线BC对称,若存在,请求出点N的坐标;若不存在,请说明理由.23. (1)、【基本模型】
(1)、【基本模型】如图1,已知 , 线段AC与BD交于点P,且P为线段BD的中点.求证:;
(2)、【应用模型】如图2,在和中, , , 且 , , 将绕点A顺时针方向旋转,把点E在AC边上时的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为 , 连接BD,点P是线段BD的中点,连接PC,PE.当在起始位置时,猜想:PC与PE的数量关系和位置关系,并说明理由;
(3)、【拓展迁移】如图3,在【应用模型】的条件下,当时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论.