山东省日照市岚山区2022年中考一模数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 下列各数中,绝对值最大的是( )A、 B、 C、 D、22. 根据第七次全国人口普查结果,日照市常住人口约为297万人,297万用科学记数法表示为( )A、 B、 C、 D、3. 如图,将直角△ABC放置在一组平行的横线格中,直角顶点C恰好落在横线上,若∠α=40°,则∠β的度数是( )
 A、40° B、45° C、50° D、60°4. 已知方程组 , 则的值是( )A、3 B、6 C、9 D、125. 下列运算正确的是( )A、 B、 C、 D、6. 如图是由几个相同的小正方体搭建成的几何体的主视图和俯视图,则搭建这个几何体所需要的小正方体的个数至少为( )
A、40° B、45° C、50° D、60°4. 已知方程组 , 则的值是( )A、3 B、6 C、9 D、125. 下列运算正确的是( )A、 B、 C、 D、6. 如图是由几个相同的小正方体搭建成的几何体的主视图和俯视图,则搭建这个几何体所需要的小正方体的个数至少为( ) A、3 B、4 C、5 D、67. 下列命题是真命题的是( )A、一个正数的算术平方根一定比这个数小 B、若 , 则 C、三角形的任意两边之和大于第三边 D、“守株待兔”是必然事件8. 如图,菱形的一边在y轴上, , , 将菱形绕原点O逆时针方向旋转75°,得到菱形 , 则顶点B的对应点的坐标是( )
A、3 B、4 C、5 D、67. 下列命题是真命题的是( )A、一个正数的算术平方根一定比这个数小 B、若 , 则 C、三角形的任意两边之和大于第三边 D、“守株待兔”是必然事件8. 如图,菱形的一边在y轴上, , , 将菱形绕原点O逆时针方向旋转75°,得到菱形 , 则顶点B的对应点的坐标是( )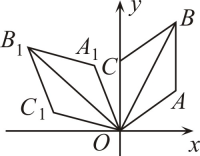 A、 B、 C、 D、9. 如图,AB是垂直于水平面的建筑物,沿建筑物底端B沿水平方向向左走8米到达点C,沿坡度i=1:2(坡度i=坡面铅直高度与水平宽度的比)斜坡走到点D,再继续沿水平方向向左走40米到达点E(A、B、C、D、E在同一平面内),在E处测得建筑物顶端A的仰角为34°,已知建筑物底端B与水平面DE的距离为2米,则建筑物AB的高度约是( )(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
A、 B、 C、 D、9. 如图,AB是垂直于水平面的建筑物,沿建筑物底端B沿水平方向向左走8米到达点C,沿坡度i=1:2(坡度i=坡面铅直高度与水平宽度的比)斜坡走到点D,再继续沿水平方向向左走40米到达点E(A、B、C、D、E在同一平面内),在E处测得建筑物顶端A的仰角为34°,已知建筑物底端B与水平面DE的距离为2米,则建筑物AB的高度约是( )(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67) A、27.1米 B、30.8米 C、32.8米 D、49.2米10. 如图,中, , , , 动点P从A点出发,沿折线以每秒5个单位长度的速度运动(运动到B点停止),过点P作于点D,则的面积y与点P运动的时间x之间的函数图象大致是( )
A、27.1米 B、30.8米 C、32.8米 D、49.2米10. 如图,中, , , , 动点P从A点出发,沿折线以每秒5个单位长度的速度运动(运动到B点停止),过点P作于点D,则的面积y与点P运动的时间x之间的函数图象大致是( )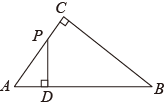 A、
A、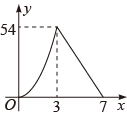 B、
B、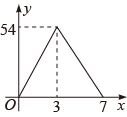 C、
C、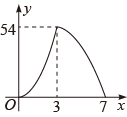 D、
D、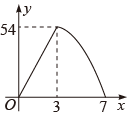 11. 如图,∠POQ=45°,点A1 , A2 , A3 , A4 , …An依次在射线OQ上,点B1 , B2 , B3 , …Bn依次在射线OP上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …△AnBnAn+1都是以A1 , A2 , A3 , A4 , …An为直角顶点的等腰直角三角形,已知OA1=1,则△A2022B2022A2023的面积是( )
11. 如图,∠POQ=45°,点A1 , A2 , A3 , A4 , …An依次在射线OQ上,点B1 , B2 , B3 , …Bn依次在射线OP上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …△AnBnAn+1都是以A1 , A2 , A3 , A4 , …An为直角顶点的等腰直角三角形,已知OA1=1,则△A2022B2022A2023的面积是( )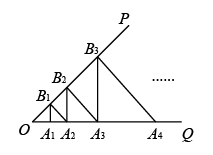 A、 B、 C、 D、12. 如图,已知二次函数的图象交x轴于 , 对称轴为 . 则下列结论:①;②;③;④若 , 是图象上的两点,则;⑤若 , 则 . 其中正确结论的个数是( )
A、 B、 C、 D、12. 如图,已知二次函数的图象交x轴于 , 对称轴为 . 则下列结论:①;②;③;④若 , 是图象上的两点,则;⑤若 , 则 . 其中正确结论的个数是( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
13. 若单项式与是同类项,则的平方根是 .14. 若不等式组无解,则m的取值范围是 .15. 如图,以边长是2的正六边形各顶点为圆心,画半径为1的圆弧,六条圆弧围成一个“六角星”,则这个“六角星”(阴影部分)的面积是 .
 16. 如图,在平面直角坐标系中,的边在x轴上,边与y轴的交点是 , 将沿y轴向右翻折,点A落在E处,连接 , 交于点F,已知 , 的面积是1.若的图象经过点E,则k的值是 .
16. 如图,在平面直角坐标系中,的边在x轴上,边与y轴的交点是 , 将沿y轴向右翻折,点A落在E处,连接 , 交于点F,已知 , 的面积是1.若的图象经过点E,则k的值是 .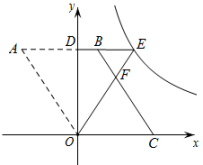
三、解答题
-
17.(1)、先化简,再求值: , 其中 .(2)、已知是关于x的一元二次方程的一个实数根,求方程的另一个根及m的值.18. 为深入落实“双减”政策,学校从九年级中的学生随机抽取男生和女生共40名,对他们周末完成书面作业的时间x(小时)进行调查,统计结果分为四档:A档:;B档:;C档:;D档: . 根据调查结果,制作了两张不完整的统计图表.其中男生周末完成书面作业的时间数据(单位:小时)如下:1.2,2.5,3.5,0.8,1,2.6,1.5,2.5,3.2,2,1.8,2.5,1.5,2.4,2.8
时间x(小时)
人数
A档:
2
B档:
5
C档:
D档:
图表1:男生周末完成书面作业时间频数分布表

图表2:女生周末完成书面作业时间扇形统计图
(1)、在频数分布表中,a= , b= , 男生周末完成书面作业时间的众数是小时;(2)、在扇形统计图中,女生周末完成书面作业时间的中位数在档(在A、B、C、D中选填);(3)、若学校在周末完成书面作业时间为D档的同学中随机抽取2名同学了解情况,请用画树状图或列表的方法,求抽取的2名同学都是女生的概率.19. 在4月22日“世界地球日”前夕,某企业计划向草原地区捐赠甲、乙两种树苗,已知甲种树苗每棵30元,乙种树苗每棵40元,且甲种树苗棵数比乙种树苗棵数的2倍多400棵,购买两种树苗的总金额为7.2万元.(1)、求计划捐赠的甲、乙两种树苗共多少棵;(2)、为保证绿化效果,该企业决定在原计划的基础上,追加捐赠甲、乙两种树苗共700棵,所有树苗的运输费等其它费用共需3000元,若保证总费用不超过10万元,则追加的甲种树苗至少有多少棵?20. 如图,是的直径,C、D是圆上的两点,且 , 的平分线交于点E,过E作的垂线,垂足为F. (1)、求证:是的切线;(2)、连接 , 交于点G,若已知 , , 求的长.21.
(1)、求证:是的切线;(2)、连接 , 交于点G,若已知 , , 求的长.21. (1)、【探究·发现】正方形的对角线长与它的周长及面积之间存在一定的数量关系.已知正方形的对角线长为a,则正方形的周长为 , 面积为(都用含a的代数式表示).(2)、【拓展·综合】如图1,若点M、N是某个正方形的两个对角顶点,则称M、N互为“正方形关联点”,这个正方形被称为M、N的“关联正方形”.
(1)、【探究·发现】正方形的对角线长与它的周长及面积之间存在一定的数量关系.已知正方形的对角线长为a,则正方形的周长为 , 面积为(都用含a的代数式表示).(2)、【拓展·综合】如图1,若点M、N是某个正方形的两个对角顶点,则称M、N互为“正方形关联点”,这个正方形被称为M、N的“关联正方形”.①在平面直角坐标系中,点P是原点O的“正方形关联点”.若 , 则O、P的“关联正方形”的周长是 ▲ ;若点P在直线上,则O、P的“关联正方形”面积的最小值是 ▲ .
②如图2,已知点 , 点B在直线上,正方形是A、B的“关联正方形”,顶点P、Q到直线l的距离分别记为a和b,求的最小值.
22. 已知抛物线与x轴交于 , 两点,交y轴于点C,点P是抛物线上一个动点,且点P的横坐标为m.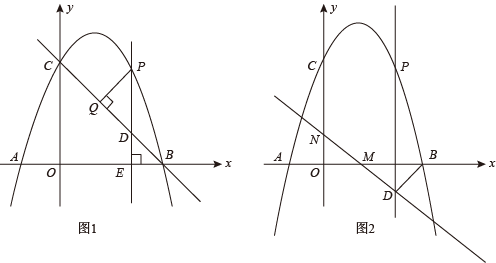 (1)、求抛物线的解析式;(2)、如图1,若点P在上方的抛物线上运动(不与B、C重合),过点P作x轴的垂线,垂足为E,交于点D,过点P作的垂线,垂足为Q,若 , 求m的值;(3)、如图2,将直线沿y轴向下平移5个单位,交x轴于点M,交y轴于点N.过点P作x轴的垂线,交直线于点D,是否存在一点P,使是等腰三角形?若存在,请直接写出符合条件的m的值;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,若点P在上方的抛物线上运动(不与B、C重合),过点P作x轴的垂线,垂足为E,交于点D,过点P作的垂线,垂足为Q,若 , 求m的值;(3)、如图2,将直线沿y轴向下平移5个单位,交x轴于点M,交y轴于点N.过点P作x轴的垂线,交直线于点D,是否存在一点P,使是等腰三角形?若存在,请直接写出符合条件的m的值;若不存在,请说明理由.