山东省青岛西海岸新区2022年九年级二模数学试题
试卷更新日期:2022-05-31 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、3 D、2. “中国结”是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.下列四个中国结图案中,既是中心对称图形又是轴对称图形的有( )
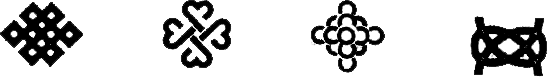 A、1个 B、2个 C、3个 D、4个3. 《2021—2022中国大数据产业发展报告》预测,未来三年,我国大数据产业市场将保持12%以上的增速,到2023年整体规模将达到11522.5亿元.11522.5亿用科学记数法可以表示为( )A、 B、 C、 D、4. 当时, , , 的大小关系是( )A、 B、 C、 D、5. 如图,线段经过平移得到线段 , 其中点 , 的对应点分别为点 , , 这四个点都在格点上.若线段上有一个点 , , 则点在上的对应点的坐标为
A、1个 B、2个 C、3个 D、4个3. 《2021—2022中国大数据产业发展报告》预测,未来三年,我国大数据产业市场将保持12%以上的增速,到2023年整体规模将达到11522.5亿元.11522.5亿用科学记数法可以表示为( )A、 B、 C、 D、4. 当时, , , 的大小关系是( )A、 B、 C、 D、5. 如图,线段经过平移得到线段 , 其中点 , 的对应点分别为点 , , 这四个点都在格点上.若线段上有一个点 , , 则点在上的对应点的坐标为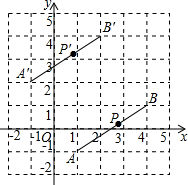 A、 B、 C、 D、6. 如图是切线,点A为切点,交于点C,点D在上,连接 , 若 , 则的度数为( )
A、 B、 C、 D、6. 如图是切线,点A为切点,交于点C,点D在上,连接 , 若 , 则的度数为( )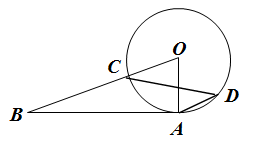 A、 B、 C、 D、7. 在平面直角坐标系中,为坐标原点,点的坐标为 , 若为轴上一点,且使得为等腰三角形,则满足条件的点有( )A、2个 B、3个 C、4个 D、5个8. 二次函数( , , 是常数,)的自变量与函数值的部分对应值如下表:
A、 B、 C、 D、7. 在平面直角坐标系中,为坐标原点,点的坐标为 , 若为轴上一点,且使得为等腰三角形,则满足条件的点有( )A、2个 B、3个 C、4个 D、5个8. 二次函数( , , 是常数,)的自变量与函数值的部分对应值如下表:…
0
1
2
…
…
2
1
2
…
下列说法错误的是( )
A、 B、和2是方程的两个根 C、 D、二次函数的图象与轴无交点二、填空题
-
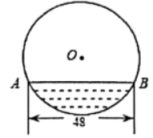
9. 不等式组的解集为 .10. 甲,乙两人进行掷飞镖比赛,每人各掷6次,所得环数的平均数相同.甲所得环数为:9,8,9,6,10,6,乙所得环数的方差为4,那么成绩较为稳定的是 . (填“甲”或“乙”)11. 扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了20%.已知去年这种水果批发销售总额为10000元,则这种水果今年每千克的平均批发价是元.12. 往直径为的圆柱形容器内装入一些水以后,截面如图,若水面宽 , 则水的最大深度为cm.
 13. 如图,在菱形中, , , 菱形的一个顶点在反比例函数的图象上,则的值为 .
13. 如图,在菱形中, , , 菱形的一个顶点在反比例函数的图象上,则的值为 .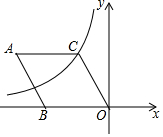 14. 如图是一张矩形纸片 , 点在边上,把沿直线对折,使点落在对角线上的点处,连接 . 若点 , , 在同一条直线上, , 则 .
14. 如图是一张矩形纸片 , 点在边上,把沿直线对折,使点落在对角线上的点处,连接 . 若点 , , 在同一条直线上, , 则 .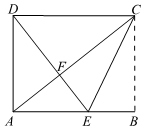
三、解答题
-
15. 求作的内切圆 .
 16.(1)、化简:;(2)、已知二次函数与正比例函数的图象只有一个交点,求的值.17. 小明和小亮做游戏,规则如下:将正面分别写有数字1,2,3,4的4张卡片背面朝上,洗匀.先从中任意抽取1张(不放回),再从余下的3张中任意抽取1张,若抽得的2张卡片上的数字之和为2的倍数则小明胜,若抽得的2张卡片上的数字之和为3的倍数则小亮胜.这个游戏对双方公平吗?请说明理由.18. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )
16.(1)、化简:;(2)、已知二次函数与正比例函数的图象只有一个交点,求的值.17. 小明和小亮做游戏,规则如下:将正面分别写有数字1,2,3,4的4张卡片背面朝上,洗匀.先从中任意抽取1张(不放回),再从余下的3张中任意抽取1张,若抽得的2张卡片上的数字之和为2的倍数则小明胜,若抽得的2张卡片上的数字之和为3的倍数则小亮胜.这个游戏对双方公平吗?请说明理由.18. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )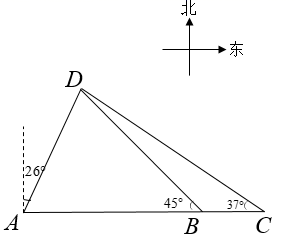 19. 某校为了解学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
19. 某校为了解学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:①七年级成绩在这一组的是:70,72,74,75,76,76,77,77,77,78,79;
②七年级成绩频数分布直方图及七、八年级成绩的平均数、中位数分别如下:

年级
平均数
中位数
七
76.9
八
79.2
79.5
根据以上信息,回答下列问题:
(1)、在这次测试中,七年级在80分以上(含80分)的有人;(2)、表中m的值为;(3)、在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(4)、该校七年级学生有500人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.20. 如图,已知过点 的直线 与直线 : 相交于点 .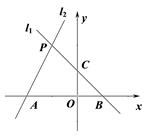 (1)、求直线 的解析式;(2)、求四边形 的面积.21. 已知是等边三角形,点 , 分别在边 , 上,且 , 过点平行于的直线与的延长线交于点 , 连接 , , .
(1)、求直线 的解析式;(2)、求四边形 的面积.21. 已知是等边三角形,点 , 分别在边 , 上,且 , 过点平行于的直线与的延长线交于点 , 连接 , , .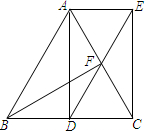 (1)、求证:;(2)、若是的中点,请判断四边形的形状,并说明理由.22. “童心迎六一,欢乐共成长”,某超市计划在儿童节期间进行一款文具的促销活动.该文具进价为5元/件,售价为9元/件时,当天的销售量为100件.在销售过程中发现:售价每下降0.5元,当天的销售量就增加5件.设当天销售单价统一为元/件( , 且是按0.5元的倍数下降),当天销售利润为元.(1)、求与的函数关系式;(2)、要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)、若每件文具的利润不超过60%,要想当天获得最大利润,每件文具的售价应为多少元?并求出最大利润.23. 问题提出:把 , , , , 五个不同的棋子放在如图所示的方格纸内,使每行每列只能出现一个棋子,共有多少种不同的放法?
(1)、求证:;(2)、若是的中点,请判断四边形的形状,并说明理由.22. “童心迎六一,欢乐共成长”,某超市计划在儿童节期间进行一款文具的促销活动.该文具进价为5元/件,售价为9元/件时,当天的销售量为100件.在销售过程中发现:售价每下降0.5元,当天的销售量就增加5件.设当天销售单价统一为元/件( , 且是按0.5元的倍数下降),当天销售利润为元.(1)、求与的函数关系式;(2)、要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)、若每件文具的利润不超过60%,要想当天获得最大利润,每件文具的售价应为多少元?并求出最大利润.23. 问题提出:把 , , , , 五个不同的棋子放在如图所示的方格纸内,使每行每列只能出现一个棋子,共有多少种不同的放法?
问题探究:为了解决上面的问题,我们先从最简单的情形入手,从中找到解决问题的方法.
探究一:
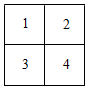
若把 , 两个不同的棋子放在方格纸内,并使每行每列只能出现一个棋子,可看成分两步完成这件事情.第一步放棋子 , 棋子可以放在4个方格的任意一个中,故棋子有4种不同的放法.第二步放棋子 , 由于棋子已放定,那么放棋子的那一行和那一列中的其他方格内也不能放棋子 , 故还剩下1个方格可以放棋子 , 棋子只有1种放法.如:棋子放在方格1中,那么方格2和方格3也不能放棋子 , 棋子只能放在方格4中.由于第一步有4种放法,第二步有1种放法,所以共有种不同放法.
探究二:
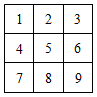
若把 , , 三个不同的模子放在方格纸内,并使每行每列只能出现一个棋子,可看成分三步完成这件事情.第一步放棋子 , 棋子可以放在9个方格的任意一个中,故棋子有9种不同的放法.第二步放棋子 , 由于棋子已放定,那么放棋子的那一行和那一列中的其他方格内也不能放棋子 , 此时只剩四个方格可以放棋子 , 且四个方格的位置可类似看作“方格”模型,所以接下来放棋子和棋子的两步有种不同的放法.由于第一步有9种放法,第二步和第三步有种放法,所以共有种不同的放法.
 (1)、探究三:
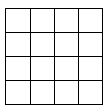
(1)、探究三:若把 , , , 四个不同的棋子放在方格纸内,可看成分四步完成这件事情.第一步放棋子 , 棋子可以放在个方格的任意一个中,故棋子有种不同的放法.第二步放棋子 , 由于棋子已放定,那么放棋子的那一行和那一列中的其他方格内也不能放棋子 , 此时只有个方格可以放棋子 , 且这些方格的位置可类似看作“方格”模型,所以接下来放棋子 , 棋子和棋子的三步有种不同的放法.所以共有种不同的放法.
 (2)、问题解决:把 , , , , 五个不同的棋子放在方格纸内,并使每行每列只能出现一个棋子,共有种不同的放法.(3)、拓展延伸:若安排甲,乙,丙,丁,戊五人分别坐在五个不同的位置上,共有种不同的坐法.24. 如图,在中, , , , 为的中点.点从点出发,沿方向匀速运动,速度为1cm/s;同时,点从点出发,沿方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.过点作 , 交的延长线于点 , 过点作 , 交于点 . 设运动时间为 , 请解答下列问题:
(2)、问题解决:把 , , , , 五个不同的棋子放在方格纸内,并使每行每列只能出现一个棋子,共有种不同的放法.(3)、拓展延伸:若安排甲,乙,丙,丁,戊五人分别坐在五个不同的位置上,共有种不同的坐法.24. 如图,在中, , , , 为的中点.点从点出发,沿方向匀速运动,速度为1cm/s;同时,点从点出发,沿方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.过点作 , 交的延长线于点 , 过点作 , 交于点 . 设运动时间为 , 请解答下列问题: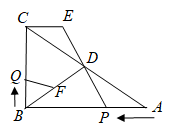 (1)、当为何值时,是直角三角形?(2)、连接 , , 设四边形的面积为 , 试确定与的函数关系式;(3)、当为何值时,四边形的面积与的面积相等?(4)、在运动过程中,是否存在某一时刻 , 使平分?若存在,求出的值;若不存在,请说明理由.
(1)、当为何值时,是直角三角形?(2)、连接 , , 设四边形的面积为 , 试确定与的函数关系式;(3)、当为何值时,四边形的面积与的面积相等?(4)、在运动过程中,是否存在某一时刻 , 使平分?若存在,求出的值;若不存在,请说明理由.